算法刷题总结 (七) 双指针
算法总结7 双指针
一、双指针的概念
1.1、什么是双指针?
顾名思议,双指针就是两个指针,但是该指针不同于 C,C++中的指针地址,而是一种记录两个索引的算法思想。
实际上,在很多简单题目中,我们经常使用单指针,比如我们通过索引来遍历某数组:
# 可以这样
for i in range(n):
print(nums[i])
# 当然也可以这样
i = 0
while i<n:
print(nums[i])
i+=1
# 这样写为了引申出双指针,因为双指针一般用while来遍历
那么双指针实际上就是有两个这样的指针,最为经典的就是二分法中的左右双指针。
left, right = 0, len(nums)-1
while left<right:
if 一定条件:
return 合适的值,一般是 l 和 r 的中点
elif 一定条件:
l+=1
else:
r-=1
# 因为 l == r,因此返回 l 和 r 都是一样的
return l
其实双指针是一个很宽泛的概念,就好像数组,链表一样,其类型会有很多很多, 比如二分法经常用到左右端点双指针。滑动窗口会用到快慢指针和固定间距指针。 因此双指针其实是一种综合性很强的类型,类似于数组,栈等。 但是我们这里所讲述的双指针,往往指的是某几种类型的双指针,而不是“只要有两个指针就是双指针了”。
有了这样一个算法框架,或者算法思维,有很大的好处。它能帮助你理清思路,当你碰到新的问题,在脑海里进行搜索的时候,双指针这个词就会在你脑海里闪过,闪过的同时你可以根据双指针的所有套路和这道题进行穷举匹配,这个思考解题过程本来就像是算法。

1.2、常见类型
指针一般情况下将分为三种类类型,分别是:
| 类型 | 特点 |
|---|---|
| 快慢指针 | 两个指针步长不同,一般情况下,快的走两步,慢的走一步 |
| 左右端点指针 | 两个指针分别指向头尾,并往中间移动,步长不确定,一般为1 |
| 区间指针 | 一般为滑动窗口,两个指针及其间距视作整体,窗口有定长有变长,每次操作窗口整体向右滑动 |
不管是哪一种双指针,只考虑双指针部分的话 ,由于最多还是会遍历整个数组一次,因此时间复杂度取决于步长,如果步长是 1,2 这种常数的话,那么时间复杂度就是 O(N),如果步长是和数据规模有关(比如二分法),其时间复杂度就是 O(logN)。并且由于不管规模多大,我们都只需要最多两个指针,因此空间复杂度是 O(1)。下面我们就来看看双指针的常见套路有哪些。
1.2.1、快慢指针
本方法需要我们对「Floyd 判圈算法」(又称龟兔赛跑算法)有所了解。
假想「乌龟」和「兔子」在链表上移动,「兔子」跑得快,「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时,如果该链表中没有环,那么「兔子」将一直处于「乌龟」的前方;如果该链表中有环,那么「兔子」会先于「乌龟」进入环,并且一直在环内移动。等到「乌龟」进入环时,由于「兔子」的速度快,它一定会在某个时刻与乌龟相遇,即套了「乌龟」若干圈。
我们可以根据上述思路来解决本题。具体地,我们定义两个指针,一快一慢。慢指针每次只移动一步,而快指针每次移动两步。初始时,慢指针在位置 head,而快指针在位置 head.next。这样一来,如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。否则快指针将到达链表尾部,该链表不为环形链表。
具体的的示意图如下,同时也可以参考相似思路的,且比较简单的例题 141. 环形链表。
1.开始,乌龟slow在起始点,兔子fast在起点的下一个点。
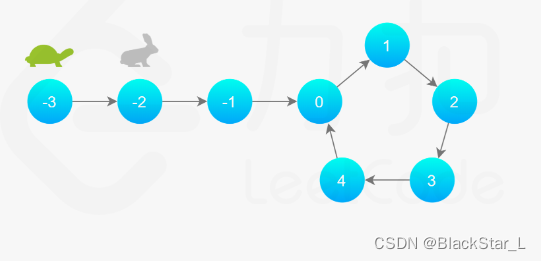
2.乌龟走得慢每次走一步,兔子走得快,每次走两步。
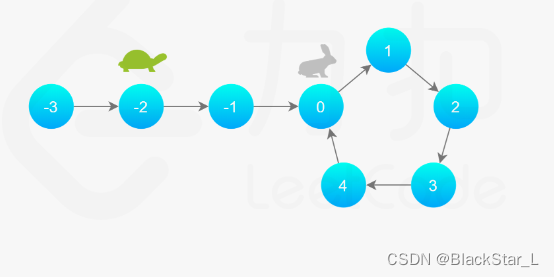
继续走,兔子先进入环。
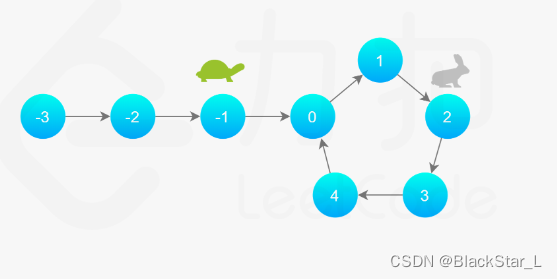
继续走,兔子一圈环快走完了,而乌龟刚进入环
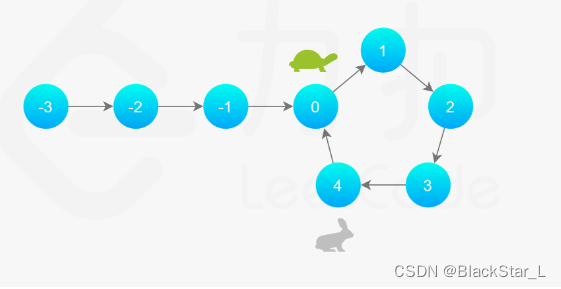
最后乌龟走第一圈的时候,兔子第二圈刚好遇上。
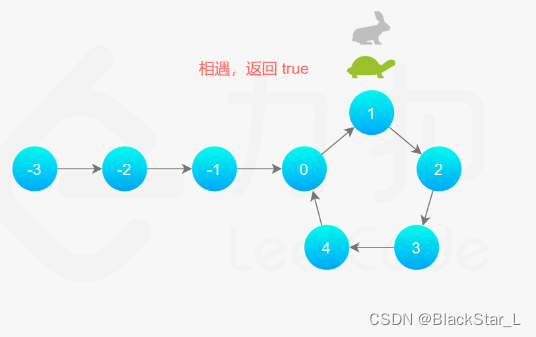
注意:
当然具体第几圈遇上是不确定的,根据步长与环的大小相关,但是乌龟与兔子在圈中循环跑时,只要步长不一致,他们之间的最近距离会不断减少,总会相遇。
但是一般情况下会设置slow走一步,fast走两步,这个设定会产生很多有规律的数学推导,比如:142. 环形链表 II 中的快慢指针做法。
细节:
为什么我们要规定初始时慢指针在位置 head,快指针在位置 head.next,而不是两个指针都在位置 head(即与「乌龟」和「兔子」中的叙述相同)?
观察下面的代码,我们使用的是 while 循环,循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合,如果我们将两个指针初始都置于 head,那么 while 循环就不会执行。因此,我们可以假想一个在 head 之前的虚拟节点,慢指针从虚拟节点移动一步到达 head,快指针从虚拟节点移动两步到达 head.next,这样我们就可以使用 while 循环了。
当然,我们也可以使用 do-while 循环或者其他方法。此时,我们就可以把快慢指针的初始值都置为 head。(所以,从这里可以得知,快慢指针初始化的值,可以相同也可以不同,具体取决于后面的判断条件)
复杂度分析:
| 时间复杂度: O ( N ) O(N) O(N),其中 N N N 是链表中的节点数。 | 空间复杂度: O ( 1 ) O(1) O(1)。 |
|---|---|
| 当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次;当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动 N N N 轮。 | 我们只使用了两个指针的额外空间。 |
题目类型:
| 问题 | 例题 | |
|---|---|---|
| 1 | 判断链表是否有环;寻找入环节点 | 141. 环形链表 | 142. 环形链表 II | 287. 寻找重复数 |
| 2 | 读写指针。将快指针的内容记录到慢指针的位置,典型的题目是原地删除(前置移动)重复元素。 | 26. 删除有序数组中的重复项 | 80. 删除有序数组中的重复项 II | 202. 快乐数 |
伪代码模板:
# 1.fast与slow初始化不同
fast, slow = head, head.next
# 有环则一定相遇 退出循环后,后面return True
while fast!=slow :
if not fast or not fast.next:
return False
slow=slow.next
fast=fast.next.next
return True
# 2.fast与slow初始化相同
# fast = slow = head
fast = head
slow = head
while fast and fast.next:
slow=slow.next
fast=fast.next.next
# 有环则一定相遇 return True
if slow == fast:
return True
return False
1.2.2、左右端点指针(相向双指针)
| 问题 | 例题 | |
|---|---|---|
| 1 | 二分查找 | 33. 搜索旋转排序数组 | 875. 爱吃香蕉的珂珂 |
| 2 | 有序数组暴力枚举。区别于上面的二分查找,这种算法指针移动是连续的,而不是跳跃性的 | 1. 两数之和 | 15. 三数之和 | 18. 四数之和 | 881. 救生艇 |
| 3 | 其他暴力枚举。比如:双边比较从大到小枚举,双边按条件枚举,无需排序或者已经有序(当然2和3其实可以归为一类) | 977. 有序数组的平方 | 75. 颜色分类(Dutch National Flag Problem) |
这一节,我们主要要讲的是1.二分查找,其他两种类型很单一,做几题便能理解。而二分法的模板形式很多,比如:循环上是否取等号,循环内left和right是否+1等等,不同的题型很多的人有不同的写法,我们能否按照自己的思维,整理出一个通用的,便于自己理解的模板呢?
* 详解二分法(二分查找 / 二分答案)
(1)二分查找:
概念:
在计算机科学中,二分查找算法也称折半搜索算法,对数搜索算法,是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半,时间复杂度是log(n)。
二分查找用于在多条记录中快速找到待查找的记录,它的思想是:每次将查找的范围缩小一半,直到最后找到记录或者找不到记录返回
二分法的使用条件:
二分法是适用于解决具有“二段性”(单调性)的问题的方法,通常表现为求解满足某一条件的最大值或者最小值问题。
- 上下界确定。 我们可以通过上下界的折半来优化查找。
- 二段性: 对某一范围内的数据,存在一个临界点,使得临界点某一侧的所有数据都满足某一性质,另一侧的所有数据都不满足这一性质,就称这一范围内的数据具有二段性。
二段性包括单调性,即区间内有序,这样二分出来的结果是严格大于或者小于或等于target的。
但是,二段性也体现在非单调性上,也称为局部有序,可以参考 162. 寻找峰值 和 33. 搜索旋转排序数组。由这些题我们可以得知,二分法的奥义(本质)不在于单调性,而是二段性。也就是我们能对整体无序但局部有序的序列进行二分法。
举例理解(有序):
给定一个数组,返回有序数组中第一个
≥
\geq
≥ target的数的位置,如果所有数都
<
\lt
<target,则返回数组长度。
暴力做法:从头开始遍历每一个数,判断是否 ≥ \geq ≥ target
高效做法:
L 和R分别指向左右边界,即闭区间。
M指向当前正在访问的数。

三种模板,比较常用第一种,其他类型也可转化为第一种。
# 左闭右闭
def bisect_search(nums, target):
left, right = 0, len(nums)-1
while left<=right:
# 循环不变量:
# nums[left-1] < target
# nums[right+1] >= target
mid = (left+right)//2
# bisect_left 加上=是bisect_right
if nums[mid]<target:
left = mid+1 # 范围缩小到 [mid+1, right]
else:
right = mid-1 # 范围缩小到 [left, mid-1]
return left # right+1
# 左闭右开
def bisect_search1(nums, target):
left, right = 0, len(nums)
while left<right:
mid = (left+right)//2
if nums[mid]<target:
left = mid+1
else:
right = mid
return left # right
# 左开右开
def bisect_search2(nums, target):
left, right = -1, len(nums)
while left+1<right:
mid = (left+right)//2
if nums[mid]<target:
left = mid
else:
right = mid
return right # left+1
输入:
nums = [1, 1, 2, 2 ,3 ,3 ,4, 4, 5]
target = 3
下面列出了四种不同类型的目标:
有序数组的二分查找分为这四种类型,这四种实际上是可以相互转换的,但为了方便,一般都转换成类型一的 lower bound 形式,即 ≥ \geq ≥ target以及它的变体。
注意:下面是以1为单位,即是在数组中都是整数时可以用的。
nums = [1, 1, 2, 2 ,3 ,3 ,4, 4, 5]
target = 3
| 序号 | 类型 | 目标 | 转换 | 输入 | 结果 | 值 |
|---|---|---|---|---|---|---|
| 类型一 | 返回第一个大于等于target的数的位置 | x ≥ \geq ≥target | x ≥ \geq ≥target | bisect_search2(nums, target) | 4 ;nums = [1, 1, 2, 2 ,3 ,3 ,4, 4, 5] | 值为从左向右第一个target的位置 |
| 类型二 | 返回第一个大于target的数的位置 | x > \gt >target | x ≥ \geq ≥(target+1) | bisect_search2(nums, target+1) | 6;nums = [1, 1, 2, 2 ,3 ,3 ,4, 4, 5] | 值为最后一个target的下一位;比第一个比target大1的位置 |
| 类型三 | 返回第一个小于target的数的位置 | x < \lt <target | (x ≥ \geq ≥target)-1 | bisect_search2(nums, target)-1 | 3;nums = [1, 1, 2, 2 ,3 ,3 ,4, 4, 5] | 第一个target的前一位;最后一个比target小1的位置 |
| 类型四 | 返回第一个小于等于target的数的位置 | x ≤ \leq ≤target | (x ≥ \geq ≥target+1)-1 | bisect_search2(nums, target+1)-1 | 5;nums = [1, 1, 2, 2 ,3 ,3 ,4, 4, 5] | 最后一个target的位置 |
有人问,怎么不讲左开右闭模板?
左开右闭这种写法一般是处理最大值的,或者说是 < 和 ≤。下面视频中讲了,这两都可以转换成 ≥,所以可以用左闭右开模板来解决。
换句话说,视频中讲的这三种二分模板,都只需关注 left right 的初始值,以及二分判定条件的写法,其余的代码都是固定的。
参考:
二分法 [bilibili]
算法—二分法详解 [cnblogs]
一个视频讲透二分查找![leetcode]
二分法总结 [csdn]
(2)二分答案:
二分查找是一种在有序数组中查找给定目标值的算法,而二分答案是一种用于求解最优化问题的算法。
二分答案通常用于求解具有单调性质的最优化问题,例如求解最大值、最小值等。根据题目要求,我们可以将二分答案分为两类:最大化答案和最小化答案。以下模板,我们可以根据实际问题进行修改。
最大化答案的二分答案模板,可行区在左侧:
def binary_answer_max():
l, r = ... # 定义搜索范围的左右边界
while l <= r:
mid = (l + r) // 2
if check(mid): # 定义一个 check 函数来检查当前的假设是否成立
l = mid + 1 # 如果成立,则更新左边界
else:
r = mid - 1 # 否则更新右边界
return r # 返回最终答案
最小化答案的二分答案模板,可行区在右侧:
def binary_answer_min():
l, r = ... # 定义搜索范围的左右边界
while l <= r:
mid = (l + r) // 2
if check(mid): # 定义一个 check 函数来检查当前的假设是否成立
r = mid - 1 # 如果成立,则更新右边界
else:
l = mid + 1 # 否则更新左边界
return l # 返回最终答案
在这两个模板中,我们都需要定义一个 check 函数来检查当前的假设是否成立。具体地,check 函数接受一个参数 mid,表示当前二分答案的中间值。check 函数需要根据实际问题进行实现,以判断当前的假设是否成立。
1.2.3、区间指针 - 滑动窗口(同向双指针)
| 区间指针 | 例题 | |
|---|---|---|
| 1 | 定长滑动窗口 | 1456. 定长子串中元音的最大数目 | 剑指 Offer 22. 链表中倒数第k个节点 |
| 2 | 变长滑动窗口 | 713. 乘积小于 K 的子数组 |
伪代码模板:
l = 0
r = k
while 没有遍历完:
自定义逻辑
l += 1
r += 1
return 合适的值
或者for循环
left = 0
for right in range(n):
自定义逻辑
while 满足某条件:
自定义逻辑
left+=1
自定义逻辑
汇总
| 快慢指针 | 左右端点指针 | 区间指针-滑动窗口 |
|---|---|---|
| 判断链表是否有环;寻找入环节点 | 二分查找 | 定长滑动窗口 |
| 读写指针。将快指针的内容记录到慢指针的位置,典型的题目是原地删除(前置移动)重复元素。 | 有序数组暴力枚举。区别于上面的二分查找,这种算法指针移动是连续的,而不是跳跃性的 | 变长滑动窗口 |
| 其他暴力枚举。比如:双边比较从大到小枚举,双边按条件枚举,无需排序或者已经有序(当然2和3其实可以归为一类) |
二、经典例题
2.1、快慢指针
| 问题 | 例题 | |
|---|---|---|
| 1 | 判断链表是否有环;寻找入环节点 | 141. 环形链表 | 142. 环形链表 II | 287. 寻找重复数 |
| 2 | 读写指针。将快指针的内容记录到慢指针的位置,典型的题目是原地删除(前置移动)重复元素 | 26. 删除有序数组中的重复项 | 80. 删除有序数组中的重复项 II | 202. 快乐数 |
(1)、链表判环
141. 环形链表
解法1:哈希表
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到我们遍历完整个链表即可。
注意:Python中的哈希表为字典和集合。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
seen = set()
# 如果有环,虽然while死循环,但一定能在while中return True
while head:
if head in seen:
return True
seen.add(head)
head = head.next
# 没有环则head的最后一个next会None而退出循环
return False
解法2:快慢指针
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
slow = head
fast = head
while fast and fast.next:
slow=slow.next
fast=fast.next.next
if fast==slow:
return True
return False
142. 环形链表 II
解法1:哈希表
思路同上
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
seen = set()
# 不允许修改表,用一个临时的指针来操作
cur = head
while cur:
if cur in seen:
return cur
seen.add(cur)
cur=cur.next
return None
解法2:快慢指针
找数学规律:当快慢指针在环中相遇,链表的起点到入环点=快慢指针相遇点到入环点的距离。
所以相遇之后,定义新的游标在链表起点,此时该游标和慢指针一起以相同步长走,相遇即到了入环点。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = fast = head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast==slow:
cur = head
while cur!=slow:
cur=cur.next
slow=slow.next
return cur
return None
287. 寻找重复数
287. 寻找重复数
这题比较巧妙的一点是将nums的每个值当做下一个点的坐标,从而进行连接起来。我们来看看这个例子:
1 4 6 6 6 2 3
值为6时会指向索引6值为3的点,再以3为索引,又指向索引为3值为6的索引。
这道题同上一题 环形链表 II 的解法一致,重复元素即表示入环点
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
fast = slow = nums[0]
# 至少存在一个重复的数,说明不会死循环,一定存在slow==fast的情况
# 不同判断是否有环,因为一定有
while True:
slow = nums[slow]
fast = nums[nums[fast]]
# 同环形链表的解法
# 1. 先记录第一次相遇
if slow == fast:
# 记录一个起点与slow一同移动直到相遇,即为入环点
cur = nums[0]
while cur!=slow:
cur = nums[cur]
slow = nums[slow]
return cur
return None
当然也有哈希表解法,同上,但时间复杂度高。
876. 链表的中间结点
慢指针走一步,快指针走两步,当快指针走到结尾,慢指针会走到链表中间。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
(2)、读写指针
26. 删除有序数组中的重复项 - 仅保留一次
26. 删除有序数组中的重复项
快指针用来判断重复,是否与前一个一样;慢指针用来存储非重复的值。
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow = fast = 1
while fast<len(nums):
if nums[fast]!=nums[slow-1]:
nums[slow]=nums[fast]
slow+=1
fast+=1
return slow
80. 删除有序数组中的重复项 II - 保留两次重复
80. 删除有序数组中的重复项 II
这里保留重复的两次,题目解法同上。数组的前两个数必然可以被保留,因此,两个指针从2开始。
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow = fast = 2
while fast<len(nums):
if nums[fast]!=nums[slow-2]:
nums[slow] = nums[fast]
slow+=1
fast+=1
return slow
递推:删除且保留k次重复
从前面两题我们可以总结出,如过要保留重复的k次:
class Solution:
def removeDuplicates(self, nums: List[int], k: int) -> int:
# 从第k个开始
slow = fast = k
while fast<len(nums):
if nums[fast]!=nums[slow-k]:
nums[slow] = nums[fast]
slow+=1
fast+=1
return slow
202. 快乐数
202. 快乐数
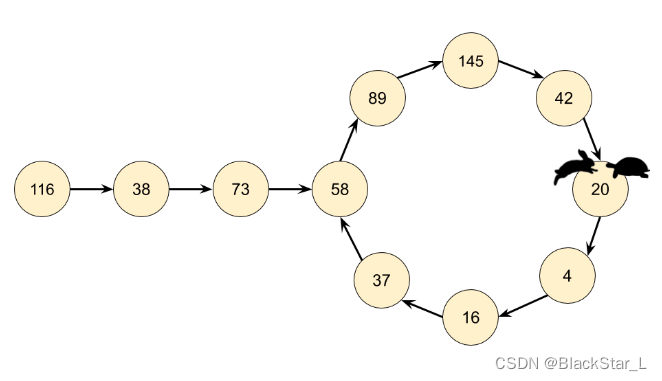
通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next 指针是通过调用 getNext(n) 函数获得。
意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法。这个算法是两个奔跑选手,一个跑的快,一个跑得慢。在龟兔赛跑的寓言中,跑的慢的称为 “乌龟”,跑得快的称为 “兔子”。
不管乌龟和兔子在循环中从哪里开始,它们最终都会相遇。这是因为兔子每走一步就向乌龟靠近一个节点(在它们的移动方向上)。
class Solution:
def isHappy(self, n: int) -> bool:
def get_next(number):
total_sum = 0
while number>0:
number, digit = divmod(number, 10)
total_sum+=digit**2
return total_sum
slow = fast = n
# fast!=1判断是否是快乐数
# fast!=slow 说明有环,进行打破死循环
# 快乐数的判断快于环的判断,所以会在打破循环前判断是否是快乐数
while fast!=1:
slow = get_next(slow)
fast = get_next(get_next(fast))
if fast==slow:
break
return fast==1
2.2、左右端点指针(相向双指针)
| 问题 | 例题 | |
|---|---|---|
| 1 | 二分查找 | 33. 搜索旋转排序数组 | 875. 爱吃香蕉的珂珂 |
| 2 | 有序数组暴力枚举。区别于上面的二分查找,这种算法指针移动是连续的,而不是跳跃性的 | 1. 两数之和 | 15. 三数之和 | 18. 四数之和 | 881. 救生艇 |
| 3 | 其他暴力枚举。比如:双边比较从大到小枚举,双边按条件枚举,无需排序或者已经有序(当然2和3其实可以归为一类) | 977. 有序数组的平方 | 75. 颜色分类(Dutch National Flag Problem) |

(1.1)、二分法
34. 在排序数组中查找元素的第一个和最后一个位置
# lower_bound 返回最小的满足 nums[i] >= target 的 i
# 如果数组为空,或者所有数都 < target,则返回 len(nums)
# 要求 nums 是非递减的,即 nums[i] <= nums[i + 1]
# 闭区间写法
def lower_bound(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # 闭区间 [left, right]
while left <= right: # 区间不为空
# 循环不变量:
# nums[left-1] < target
# nums[right+1] >= target
mid = (left + right) // 2
if nums[mid] < target:
left = mid + 1 # 范围缩小到 [mid+1, right]
else:
right = mid - 1 # 范围缩小到 [left, mid-1]
return left # 或者 right+1
# 左闭右开区间写法
def lower_bound2(nums: List[int], target: int) -> int:
left = 0
right = len(nums) # 左闭右开区间 [left, right)
while left < right: # 区间不为空
# 循环不变量:
# nums[left-1] < target
# nums[right] >= target
mid = (left + right) // 2
if nums[mid] < target:
left = mid + 1 # 范围缩小到 [mid+1, right)
else:
right = mid # 范围缩小到 [left, mid)
return left # 或者 right
# 开区间写法
def lower_bound3(nums: List[int], target: int) -> int:
left, right = -1, len(nums) # 开区间 (left, right)
while left + 1 < right: # 区间不为空
mid = (left + right) // 2
# 循环不变量:
# nums[left] < target
# nums[right] >= target
if nums[mid] < target:
left = mid # 范围缩小到 (mid, right)
else:
right = mid # 范围缩小到 (left, mid)
return right # 或者 left+1
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
start = lower_bound(nums, target) # 选择其中一种写法即可
if start == len(nums) or nums[start] != target:
return [-1, -1]
# 如果 start 存在,那么 end 必定存在
end = lower_bound(nums, target + 1) - 1
return [start, end]
33. 搜索旋转排序数组 - (非有序序列)
但是这道题中,数组本身不是有序的,进行旋转后只保证了数组的局部是有序的,这还能进行二分查找吗?答案是可以的。
可以发现的是,我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。拿示例来看,我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分,其中左边 [4, 5, 6] 这个部分的数组是有序的,其他也是如此。
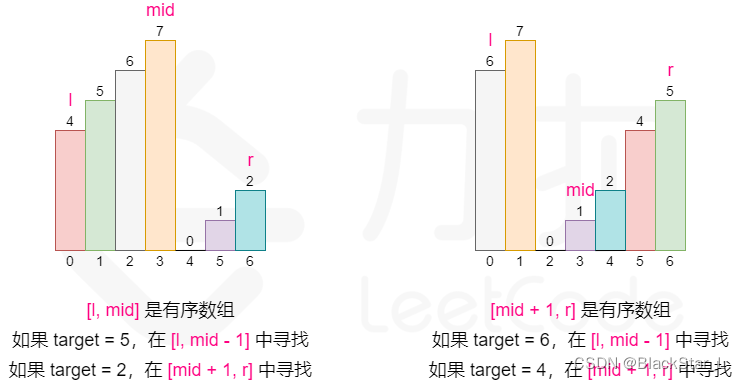
这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部分:
如果 [l, mid - 1] 是有序数组,且 target 的大小满足 [nums[l],nums[mid]),则我们应该将搜索范围缩小至 [l, mid - 1],否则在 [mid + 1, r] 中寻找。
如果 [mid, r] 是有序数组,且 target 的大小满足 (nums[mid+1],nums[r]],则我们应该将搜索范围缩小至 [mid + 1, r],否则在 [l, mid - 1] 中寻找。
class Solution:
def search(self, nums: List[int], target: int) -> int:
l, r = 0, len(nums)-1
while l<=r:
mid = (l+r)//2
if nums[mid]==target:
return mid
else:
# 以有序序列为分界线,进行两次二分,需要区分有顺序的两个部分
# [4,5,6,7,0,1,2]
# 说明在左半区 [4,5,6,7]
if nums[0]<=nums[mid]:
# 在该半区之中再去二分,以mid为中点
# 在左半边[4]
if nums[0]<=target<nums[mid]:
r = mid - 1
# 在右半边[5,6,7]
else:
l = mid + 1
# [5,6,7,0,1,2,4]
# 否则在右半区 [0,1,2,4]
else:
# [1,2,4]
if nums[mid]<target<=nums[len(nums)-1]:
l = mid+1
# [0]
else:
r = mid-1
return -1
162. 寻找峰值 - (非有序序列)
162. 寻找峰值
无序数组在满足某些规律时,也是可以使用二分法的。详情可以参考其他博客去理解这个二段性。
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
left, right = 0, len(nums)-1
while left<right:
mid = (left+right)//2
# 右边大,左边界左移
if nums[mid]<nums[mid+1]:
left = mid+1
# 右边小,则下坡了,往左找峰值
# 这里不能-1,因为该mid可能是峰值
else:
right = mid
return left
475. 供暖器 (使用python库 bisect)
475. 供暖器
Python的bisect库是使用二分法,将指定的值插入(预插入而不是真实插入,真实插入需要insort()函数),返回位置,bisect默认如果值相等则插入到相同的值的右侧,其余情况按顺序插入返回索引。
所以,当我们将house插入到排好序的heaters中时,可能house与heaters中的某个位置的值相等,被插入到右边,那么它的真实位置实际上变大了一位,所以我们需要减去1,;但有时候,house与heaters中的某个位置的值不相等,被插入到右边是正确的位置,不用做改变。
对于上面两种情况,我们没办法直接判断,只能直接将两个位置都取出来对比做判断,按照题意,取house与heater的值的差值,取其中较小的。但注意,插入到右侧时,索引不能大于heaters的最大长度;退一位时,索引不能小于0。
最后取所house到所有heaters的距离的最大值即可。
import bisect
class Solution:
def findRadius(self, houses: List[int], heaters: List[int]) -> int:
heaters.sort()
max_radius = 0
for house in houses:
right = bisect.bisect(heaters, house)
left = right-1
right_radius = heaters[right]-house if right<len(heaters) else float('inf')
left_radius = house-heaters[left] if left>-1 else float('inf')
max_radius = max(max_radius, min(right_radius, left_radius))
return max_radius
常规二分写法:
class Solution:
def findRadius(self, houses: List[int], heaters: List[int]) -> int:
def find_bisect(nums, target):
left, right = 0, len(nums)-1
while left<=right:
mid = (left+right)//2
# print(left, right, nums, target)
if target>nums[mid]:
left=mid+1
else:
right=mid-1
return left
# heaters是乱序的,先排序
heaters.sort()
dis = 0
# 使用二分法,寻找离每个house最近的heaters?实际上不完全是...
# (下面的二分实际上是找比该house大或相等的heater) >=target
# 如果位置值相等,那就是最近距离,这没错。
# 那如果位置值不相等,就会出现错位现象。
# 比如[1,2,3,4]与[1,4],target为2时,在[1,4]中>=2的位置为index=1
# 而index=1的位置的值为4,但是2明显离1更近而不是离找的4更近。
# 所以对于每个index,它并不是最近的位置值,相等或者小1的位置才是。
# house与相应的heater做减法,取最大值
for house in houses:
res = find_bisect(heaters, house)
right = res
# 比house大或相等的位置值为right,所以left一定比house小
# 所以是 house-heaters[left]
left = right-1 if right>=0 else right
right_radius = heaters[right]-house if res<len(heaters) else float('inf')
left_radius = house-heaters[left] if left>-1 else float('inf')
nearest = min(right_radius, left_radius)
# print(house, nearest)
dis = max(dis, nearest)
return dis
(1.2)、二分答案
购物系统的降级策略
实习笔试-第一题-购物系统的降级策略
二分答案的思路很简单:
首先根据题目,我们很明显的确定了答案的上界和下界,于是我们需要快速找到其中的某个值,而满足题目要求的最大或最小的某条件,遍历明显不如二分法而来的快,所以代码整体是二分的思路。
nums = list(map(int, input().split()))
max_volumn = int(input())
if sum(nums)<=max_volumn:
print(-1)
else:
left, right = 0, max(nums)
def check(mid):
s = sum(mid if i>mid else i for i in nums)
return s<=max_volumn
while left<=right:
mid = (left+right)//2
if check(mid):
left=mid+1
else:
right=mid-1
print(right)
875. 爱吃香蕉的珂珂
875. 爱吃香蕉的珂珂
这一题要注意一点,当sum_time==h时,不能直接return mid,因为比如:math.ceil(10/5)到math.ceil(10/9)这个5-9与10相除向上取整结果都为2,但是珂珂喜欢慢慢吃,也就是吃的尽量少一点,所以要取最小值5,所以,我们在sum_time==h时,试探性的将right=mid-1,而不是直接return mid。
最后退出循环后,l>=r,之所以会大,因为sum_time==h后的right=mid-1不成功,下一次循环l=mid+1而加回来,无法在变小了,所以最后返回return l 而不是 r。
class Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
def check(mid):
s = sum(i//mid+1 if i%mid else i//mid for i in piles)
return s<=h
left, right = 1, max(piles)
while left<=right:
mid = (left+right)//2
if check(mid):
right=mid-1
else:
left=mid+1
return left
组装最大可靠性设备
from collections import defaultdict
money, type_ = list(map(int, input().split()))
n = int(input())
# 寻找二分答案的上下界
left, right = float('inf'), -float('inf')
# 按照类型存进字典
details = defaultdict(list)
for i in range(n):
tye, reli, pay = list(map(int, input().split()))
details[tye].append((reli, pay))
left, right = min(left, reli), max(right, reli)
# 按照可靠性与价格排序
for d in details:
details[d].sort()
# 计算最低可靠性的能购买的器械的价格总和
lowest_standard = 0
count = 0
for d in details:
lowest_standard += details[d][0][-1]
count+=1
# 最低可靠性的价格都高于预算,或者缺少全套的器械
if lowest_standard>money or count!=type_:
print(-1)
# 否则,进行二分答案
else:
def check(mid):
paid = 0
for d in details:
for reli, pay in details[d]:
# 找到第一个可靠的,并购买
if reli>=mid:
paid+=pay
break
else:
return False
return paid<=money
while left<=right:
mid = (left+right)//2
if check(mid):
left=mid+1
else:
right=mid-1
print(right)
最佳植树距离
n = int(input())
trees = sorted(list(map(int, input().split())))
plan = int(input())
left, right = 1, max(trees)-min(trees)
def check(mid):
count = 1
start = trees[0]
for i in range(1, n):
if trees[i]-start>=mid:
count+=1
start=trees[i]
return count>=plan
while left<=right:
mid=(left+right)//2
if check(mid):
left=mid+1
else:
right=mid-1
print(right)
食堂供餐
time = int(input())
ready = int(input())
people = list(map(int, input().split()))
def check(mid):
r = ready
for p in people:
if r<p:
return False
r += mid-p
return True
left, right = 0, sum(people)
while left <= right:
mid = (left+right)//2
if check(mid):
right = mid-1
else:
left = mid+1
print(left)
数据最节约的备份方法 - 二分答案+dfs
files = list(map(int, input().split(',')))
# 优化1,降序排序,先排大的,那么dfs就会大大缩短时间
files.sort(reverse=True)
# 二分答案
n = len(files)
# 最少一个光盘都不需要,最多每个文件装一个光盘
left, right = 0, n
def dfs(buckets, ind):
if ind == n:
return True
for i, bucket in enumerate(buckets):
if i>0 and bucket==buckets[i-1]:
continue
if files[ind]+bucket<=500:
buckets[i]+=files[ind]
if dfs(buckets, ind+1):
return True
buckets[i]-=files[ind]
return False
# 装满,用01背包,但是光盘不一定装满
# 用暴力深搜,能否将所有files装入指定数量的光盘
def check(mid):
buckets = [0]*mid
return dfs(buckets, 0)
while left<=right:
mid = (left+right)//2
# mid数量的光盘能否把所有文件都装进去
# 那么试着把mid数量减少
# 最小化答案
if check(mid):
right = mid-1
else:
left = mid+1
print(left)
(2)、有序数组暴力枚举 - N数和问题
已知一组数组和一个目标值target,求不重复的在数组中取N个数的和为target的组合。
一般做这样的题的思路是用双指针,分别指向数组的左右两端,并且,数组需要排好序,从小到大。
因为排序后,左右指针才能有规律的移动,比如:当left+right的值大于target,说明他们两个太大了,需要减小,那么只能通过right左移来减小总体值(为什么不让left左移呢?因为不能重复取,之前取过了,就要移向新的值);当left+right的值小于target,那么只能通过left右移来增加总体值。
当然,当left+right的值等于target,即为结果。

167. 两数之和 II - 输入有序数组
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left, right = 0, len(numbers)-1
# 题目说答案一定存在,那么也可以while True
while left<right:
if numbers[left]+numbers[right]>target:
right-=1
elif numbers[left]+numbers[right]<target:
left+=1
else:
return [left+1, right+1]
1. 两数之和
这题与上一题有区别,是乱序的。为了使用左右端点双指针,需要排序,并且题目不是求结果而是求原索引,所以需要在排序前记录原索引。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
num_ind = []
# 值与坐标进行绑定
for ind, val in enumerate(nums):
num_ind.append([val, ind])
num_ind.sort(key=lambda x:x[0])
# 开始双指针
left, right = 0, len(nums)-1
while left<right:
# 三个条件,>target, <target, =target
if num_ind[left][0]+num_ind[right][0]>target:
right-=1
elif num_ind[left][0]+num_ind[right][0]<target:
left+=1
else:
return [num_ind[left][1], num_ind[right][1]]
return []

15. 三数之和
咱们利用上一题的函数两数之和,每次遍历第一个数,该第一个数的后面的数求两数之和,与第一个数相加为target则保存为结果。
直接循环:
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
n = len(nums)
ans = []
for first in range(n-2):
if first>0 and nums[first]==nums[first-1]:
continue
# 优化1,最小的三个数都大于0,那么后面不可能由小于等于0的组合
if nums[first]+nums[first+1]+nums[first+2]>0:
# 这里是break,因为后面nums[first]只会变大
break
# 优化2,最小的数加上最大的两个数都小于零,那么不会再有大于等于零的组合
if nums[first]+nums[n-1]+nums[n-2]<0:
# 这里是continue,因为后面nums[first]后面还会变大
continue
left = first+1
right = n-1
while left<right:
s = nums[first]+nums[left]+nums[right]
if s < 0:
left+=1
elif s>0:
right-=1
else:
ans.append([nums[first], nums[left], nums[right]])
# 排除重复元素
left+=1
while left<right and nums[left]==nums[left-1]:
left+=1
right-=1
while right>left and nums[right]==nums[right+1]:
right-=1
return ans
写成函数:
可以自行加上上面代码的两个优化。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
# 类似于两数之和
def twoSum(start, target):
res = []
left, right = start, len(nums)-1
while left<right:
#(注意不是left>0)因为起始点不是0而是start
if left>start and nums[left]==nums[left-1]:
left+=1
continue
if right<len(nums)-1 and nums[right]==nums[right+1]:
right-=1
continue
if nums[left]+nums[right]>target:
right-=1
elif nums[left]+nums[right]<target:
left+=1
else:
res.append([nums[left],nums[right]])
right-=1
left+=1
return res
# 这里减去2,也就是至少保证剩下两个数在-1和-2。当然也可以不减
for start in range(len(nums)-2):
# 重复的需要去掉 [-1, -1, 0, 1] 这里前面两个-1都会取到后面的[0,1]
if start>0 and nums[start]==nums[start-1]:
continue
# 这里除了left和right(去掉right,一定为len(nums)无需传入)
# 第三个参数传入负的值,因为三数和为零
# 在传入个起始坐标,
twolist = twoSum(start+1, -nums[start])
for twol in twolist:
if sum(twol+[nums[start]])==0:
res.append(twol+[nums[start]])
return res
18. 四数之和
18. 四数之和
这题同样利用上前面两数之和与三数之和,层层嵌套,最内层还是两数之和。外面两层的三数之和与四数之和分别与两数之和相加,为target则return或者保存为最终的结果。
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
res = []
nums.sort()
# 相同的两数之和
def twoSum(start, target):
res = []
left, right = start, len(nums)-1
while left<right:
if left>start and nums[left]==nums[left-1]:
left+=1
continue
if right<len(nums)-1 and nums[right]==nums[right+1]:
right-=1
continue
if nums[left]+nums[right]>target:
right-=1
elif nums[left]+nums[right]<target:
left+=1
else:
res.append([nums[left],nums[right]])
left+=1
right-=1
return res
# 相同的三数之和
def threeSum(start, target):
res = []
for sec in range(start, len(nums)):
if sec>start and nums[sec]==nums[sec-1]:
continue
twolist = twoSum(sec+1, target-nums[sec])
for twol in twolist:
if sum(twol+[nums[sec]])==target:
res.append(twol+[nums[sec]])
return res
# 可以减3,也可以不减
for start in range(len(nums)-3):
if start>0 and nums[start]==nums[start-1]:
continue
threelist = threeSum(start+1, target-nums[start])
for threel in threelist:
if sum(threel+[nums[start]])==target:
res.append(threel+[nums[start]])
return res
递推:N数之和
我们可以发现,除了最内层的两数之和这个函数,其他函数可以层层嵌套,写成递归形式,于是我们整理如下:
def nSum(nums, start, target, k):
res = []
# 大于两数之和的层层嵌套
if k>2:
for i in range(start, len(nums)):
if i>start and nums[i]==nums[i-1]:
continue
nlist = nSum(nums, i+1, target-nums[i],k-1)
for nl in nlist:
if sum(nl+[nums[i]])==target:
res.append(nl+[nums[i]])
# 两数之和
else:
left, right = start, len(nums)-1
while left<right:
if left>start and nums[left]==nums[left-1]:
left+=1
continue
if right<len(nums)-1 and nums[right]==nums[right+1]:
right-=1
continue
if nums[left]+nums[right]>target:
right-=1
elif nums[left]+nums[right]<target:
left+=1
else:
res.append([nums[left],nums[right]])
right-=1
left+=1
return res
# 四数之和
nums = [1,0,-1,0,-2,2]
k = 4
target = 0
start = 0
# [[1, 2, -1, -2], [0, 2, 0, -2], [0, 1, 0, -1]]
# 三数之和
nums = [-1,0,1,2,-1,-4]
k = 3
nums.sort()
target = 0
start = 0
k = 3
# 函数入口
nSum(nums, start, target, k)
16. 最接近的三数之和
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
nums.sort()
n = len(nums)
best = 10**7
# 根据差值的绝对值来更新答案
def update(cur):
nonlocal best
if abs(cur - target) < abs(best - target):
best = cur
# 枚举 a
for i in range(n):
# 保证和上一次枚举的元素不相等
if i > 0 and nums[i] == nums[i - 1]:
continue
# 使用双指针枚举 b 和 c
j, k = i + 1, n - 1
while j < k:
s = nums[i] + nums[j] + nums[k]
# 如果和为 target 直接返回答案
if s == target:
return target
update(s)
if s > target:
# 如果和大于 target,移动 c 对应的指针
k0 = k - 1
# 移动到下一个不相等的元素
while j < k0 and nums[k0] == nums[k]:
k0 -= 1
k = k0
else:
# 如果和小于 target,移动 b 对应的指针
j0 = j + 1
# 移动到下一个不相等的元素
while j0 < k and nums[j0] == nums[j]:
j0 += 1
j = j0
return best

881. 救生艇
class Solution:
def numRescueBoats(self, people: List[int], limit: int) -> int:
people.sort()
light,heavy = 0, len(people)-1
count = 0
while light<=heavy:
if people[light]+people[heavy]<=limit:
light+=1
heavy-=1
else:
heavy-=1
count+=1
return count
(3)、其他暴力枚举

75. 颜色分类 - 类似于荷兰国旗问题
75. 颜色分类
两个左右指针分别用来存储0和2,遍历nums,找到0则与左指针交换,找到2则与右指针交换,注意相同值的交换[2,1,2],所以需要判断交换后nums[i]是否还为原值,除此之外,需要防止越界,内部要加上判断条件 i<=p2。
class Solution:
def sortColors(self, nums: List[int]) -> None:
n = len(nums)
p0, p2, i = 0, n-1, 0
while i<=p2:
# 防止 [2,1,2],if改为while
# 防止 [2,2,2],p2一直-1小于0越界,加上while i<=p2
while i<=p2 and nums[i]==2:
nums[i], nums[p2] = nums[p2], nums[i]
p2-=1
if nums[i]==0:
nums[i], nums[p0] = nums[p0], nums[i]
p0+=1
i+=1
return nums
977. 有序数组的平方
977. 有序数组的平方
两端的平方为最大值,每次将最大值放入一个新生成的list的从右到左放置。
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
n = len(nums)
ans = [0]*n
left,right,pos = 0, n-1,n-1
while left<=right:
if nums[left]**2>nums[right]**2:
ans[pos]=nums[left]**2
left+=1
else:
ans[pos]=nums[right]**2
right-=1
pos-=1
return ans
11. 盛最多水的容器
11. 盛最多水的容器
哪边短移动哪个,一样长移动任意一个。
class Solution:
def maxArea(self, height: List[int]) -> int:
# 从左右两侧边缘开始向内计算最大面积
l, r = 0, len(height)-1
area = 0
while l<r:
# 面积的计算,取较短的一个边界,长方形计算公式
area = max((r-l)*min(height[r], height[l]),area)
# 移动较短的边界,试图去寻找较高的边界
# 边界向内移动会造成宽度减少,每次移动-1,面积相对减小
# 但是同时也能找到较大的高度去弥补缺失的宽度,甚至提升总面积
if height[l]>=height[r]:
r-=1
else:
l+=1
return area
42. 接雨水
42. 接雨水
前后缀分解:
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
pre_sum = [0]*n
pre_sum[0]=height[0]
# 记录前缀
for i in range(1, n):
pre_sum[i] = max(height[i], pre_sum[i-1])
# 记录后缀
suf_sum = [0]*n
suf_sum[-1]=height[-1]
for i in reversed(range(n-1)):
suf_sum[i] = max(height[i], suf_sum[i+1])
# 开始遍历答案
ans = 0
# 取短板减去高度,剩余的为能装的水的容量
for h, pre, suf in zip(height, pre_sum, suf_sum):
ans+= min(pre, suf)-h
return ans
双指针(类似前面盛水最多的容器):
这个做法的复杂度也是O(n),但是空间复杂度降维O(1)。
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
left = 0
right = n-1
ans = 0
# 因为只用最大值,所以取代列表,只用一个变量保存最大值即可,每次计算实时更新
pre_max = 0
suf_max = 0
# 这里加上等号,left和right相等时也是一个区间柱子
while left<=right:
# 每次更新左板和右板与其之前的最大值
# 中间如果有更高的呢?那计算还是按照短板取值
# 如果中间有更矮的呢?忽略掉,被高的板子包围,容量以高的为准
pre_max = max(pre_max, height[left])
suf_max = max(suf_max, height[right])
# 两边板子比较,矮的为最大容量计算容积
if pre_max<suf_max:
ans += pre_max-height[left]
left+=1
else:
ans += suf_max-height[right]
right-=1
return ans
2.3、区间指针 - 滑动窗口 (同向双指针)
| 固定间距指针 | 例题 | |
|---|---|---|
| 1 | 定长滑动窗口 | 1456. 定长子串中元音的最大数目 | 剑指 Offer 22. 链表中倒数第k个节点 |
| 2 | 变长滑动窗口 | 209. 长度最小的子数组 | 713. 乘积小于 K 的子数组 | 3. 无重复字符的最长子串 |
(1)、定长滑动窗口
1456. 定长子串中元音的最大数目
先求出从起点开始定长窗口,每次移动,去掉首部,加上尾部。
class Solution:
def maxVowels(self, s: str, k: int) -> int:
def isVowel(ch):
return int(ch in 'aeiou')
count = 0
for i in range(k):
if isVowel(s[i]):
count+=1
ans = count
for i in range(k, len(s)):
count = count-isVowel(s[i-k])+isVowel(s[i])
ans = max(ans, count)
return ans
剑指 Offer 22. 链表中倒数第k个节点
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
left = right = head
while k:
right=right.next
k-=1
while right:
left=left.next
right=right.next
return left
(2)、变长滑动窗口
1004. 最大连续1的个数 III
1004. 最大连续1的个数 II
题意转换。把「最多可以把 K 个 0 变成 1,求仅包含 1 的最长子数组的长度」转换为 「找出一个最长的子数组,该子数组内最多允许有 K 个 0 」。
class Solution:
def longestOnes(self, nums: List[int], k: int) -> int:
left= 0
count_zero = 0
max_len = 0
for right in range(len(nums)):
if nums[right]==1:
pass
elif nums[right]!=1 and count_zero<k:
count_zero+=1
else:
while nums[left]!=0:
left+=1
left+=1
max_len = max(max_len, right-left+1)
return max_len
209. 长度最小的子数组 - (从符合条件到不符合条件)
209. 长度最小的子数组
while循环从满足条件变成不满足条件,保持单调性。一旦不满足条件,小于target,则比较子数组长度。
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
left = 0
ans = 0
res = float('inf')
for right in range(len(nums)):
ans+=nums[right]
while ans-nums[left]>=target:
ans-=nums[left]
left+=1
if ans>=target:
res = min(res, right-left+1)
return res if res!=float('inf') else 0
713. 乘积小于 K 的子数组 - (从不符合条件到符合条件)
713. 乘积小于 K 的子数组
本题采用的是双指针滑动窗口,大循环是右指针的移动,内部小循环是左指针的移动。
关键点是组合的计数:
假设子数组两个端点是 l 和 r,以r为固定右端点的所有子数组组合为:
[l, r],[l+1, r],…,[r, r]
组合总数为:[r-l+1]
大于等于k都不符合条件,直到符合小于k时开始计数。
for做法:
class Solution:
def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
if k<=1:
return 0
count = 0
left = 0
prod = 1
for right, v in enumerate(nums):
prod *= v
# 如果去掉前面 if k<=1 则加上下面这段
# left<=right and
# 因为当k=0或1时,prod无论除以哪个数不会有小于k的leftUI一直+1直到越界
while prod>=k:
prod/=nums[left]
left+=1
count += right-left+1
return count
while做法:
class Solution:
def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
left = right =0
# 记录组合个数
ans = 0
# 记录乘积
mul = 1
while right<len(nums):
mul*=nums[right]
# 防止left一直+而越界,需要left<=right
while mul>=k and left<=right:
mul/=nums[left]
left+=1
#每次右指针位移到一个新位置,应该加上 x 种数组组合:
# nums[right]
# nums[right-1], nums[right]
# nums[right-2], nums[right-1], nums[right]
# nums[left], ......, nums[right-2], nums[right-1], nums[right]
ans+=right-left+1
right+=1
return ans
3. 无重复字符的最长子串 - 只增不减
3. 无重复字符的最长子串
1.使用Count来计数重复:
from collections import Counter
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
cnt = Counter()
left = 0
ans = 0
for right, v in enumerate(s):
cnt[v]+=1
while cnt[v]>1:
cnt[s[left]]-=1
left+=1
ans = max(ans, right-left+1)
return ans
2.因为无重复,使用set哈希来记录:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
collect = set()
left = 0
count = 0
for right, v in enumerate(s):
if v not in collect:
collect.add(v)
else:
while v in collect:
collect.remove(s[left])
left+=1
collect.add(v)
count = max(count, right-left+1)
return count
2.4、其他类型指针
(1)、中间开花
5. 最长回文子串
5. 最长回文子串
回文中点可能是一个字符或者两个字符,以这为起点,两个左右指针分别扩散切判断是否相等,达到临界条件则存储和比较最大回文串。
class Solution:
def longestPalindrome(self, s: str) -> str:
max_len = ''
def findp(left, right):
while left>=0 and right<len(s) and s[left]==s[right]:
left-=1
right+=1
nonlocal max_len
max_len = max(max_len, s[left+1:right], key=len)
for i in range(len(s)):
findp(i,i)
findp(i,i+1)
return max_len
(2)、快慢指针变体
392. 判断子序列
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
ind1 = ind2 = 0
m, n = len(s), len(t)
while ind1<m and ind2<n:
if s[ind1]==t[ind2]:
ind1+=1
ind2+=1
return ind1==m
(3)、从尾向头逆序
88. 合并两个有序数组
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
m-=1
n-=1
s = len(nums1)-1
while n>=0:
while m>=0 and nums1[m]>nums2[n]:
nums1[s], nums1[m]=nums1[m], nums1[s]
m-=1
s-=1
nums1[s], nums2[n] = nums2[n], nums1[s]
n-=1
s-=1
print(nums1)
三、相似题练习
2730. 找到最长的半重复子字符串
2730. 找到最长的半重复子字符串
解法1,暴力:
class Solution:
def longestSemiRepetitiveSubstring(self, s: str) -> int:
n = len(s)
ans = 1
for i in range(n):
for j in range(i):
count = 0
sub = s[j:i+1]
# 判断子串是否半重复
for k in range(1, len(sub)):
if sub[k]==sub[k-1]:
count+=1
# 说明是半重复子串
if count<=1:
ans = max(ans, i-j+1)
return ans
解法二,变长滑动窗口:
class Solution:
def longestSemiRepetitiveSubstring(self, s: str) -> int:
n = len(s)
ans = 1
for i in range(n):
for j in range(i):
count = 0
sub = s[j:i+1]
# 判断子串是否半重复
for k in range(1, len(sub)):
if sub[k]==sub[k-1]:
count+=1
# 说明是半重复子串
if count<=1:
ans = max(ans, i-j+1)
return ans
2861. 最大合金数
class Solution:
def maxNumberOfAlloys(self, n: int, k: int, budget: int, composition: List[List[int]], stock: List[int], cost: List[int]) -> int:
def check(m):
for com in composition:
accu = 0
for money, s, c in zip(com, stock, cost):
if s<money*m:
accu += c*(money*m-s)
if accu>budget:
break
else:
return True
return False
left = 0
# 注意上界,过大可能超时
right = budget + min(stock)
while left<=right:
mid = (left+right)//2
if check(mid):
left = mid + 1
else:
right = mid - 1
# print(left, right)
return right
无限数组的最短子数组 - 找规律缩短数组
参考
官方解题 环形链表
快慢指针
官方解题 搜索旋转排序数组
713.官方思路秒懂○注释详细○双指针滑窗 【附通用滑窗模板】