matlab绘图学习(二维曲线)
目录
函数
前言
所有程序均已经经过调试,本篇文章为记录自己学习matlab的过程
plot函数
一、plot函数的基本用法:
plot(x,y)
其中,x,y分别存储x坐标和y坐标数据
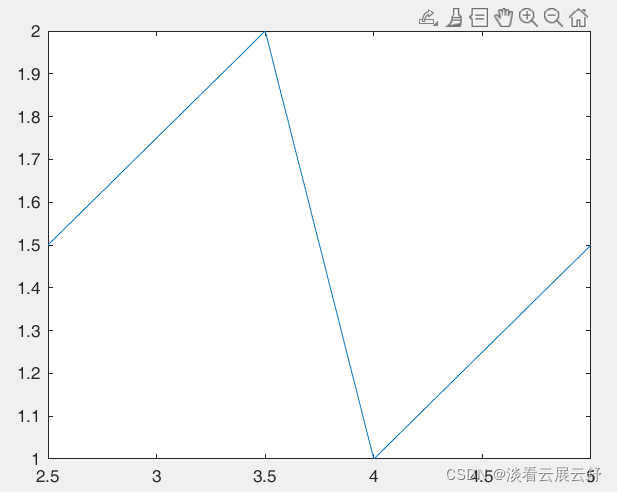
例子:绘制一条折线:
>> x=[2.5,3.5,4,5];
>> y=[1.5,2,1,1.5];
>> plot(x,y)二、 plot函数的调用格式
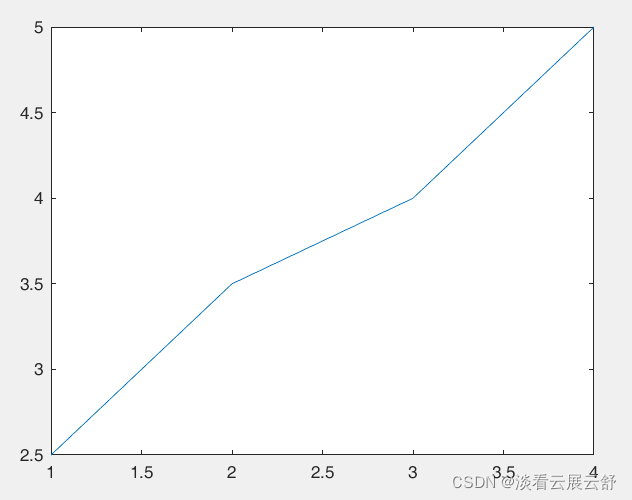
(1)最简单的调用plot(x)
>> x=[2.5,3.5,4,5]; >> plot(x)
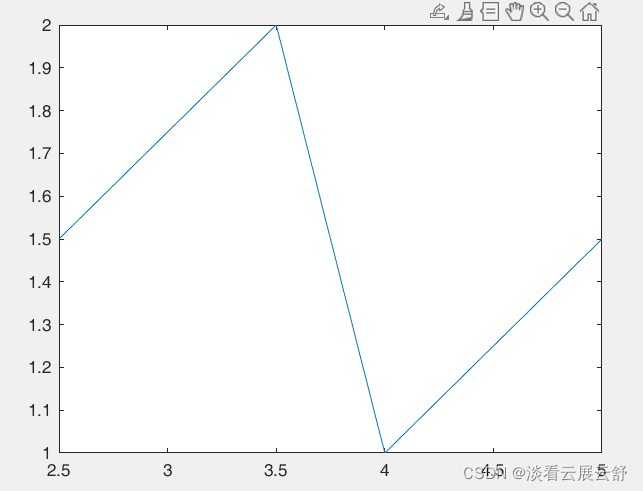
(2)当plot函数的参数x是复数向量时,则分别以该向量元素的实部和虚部为横、纵坐标绘制出一条曲线
复数(实为横,虚为纵)
>> x=[2.5,3.5,4,5]; >> y=[1.5,2,1,1.5]; >> cx=x+y*i; >> plot(cx)程序也可将cx=x+y*i;换成cx=complex(x,y);有一样的效果
(3)plot(x,y)函数参数的变化形式
当x是向量,y是矩阵时:矩阵的列数等于x的长度,则以向量x为横坐标,以y的行向量为纵坐标绘制曲线,曲线条数等于y的行数。
矩阵的行数等于x的长度,则以向量x为横坐标,以y的列向量为纵坐标绘制曲线,曲线条数等于y的列数。
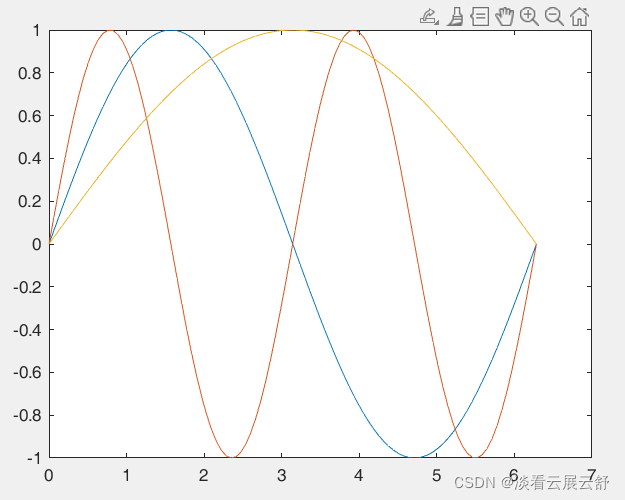
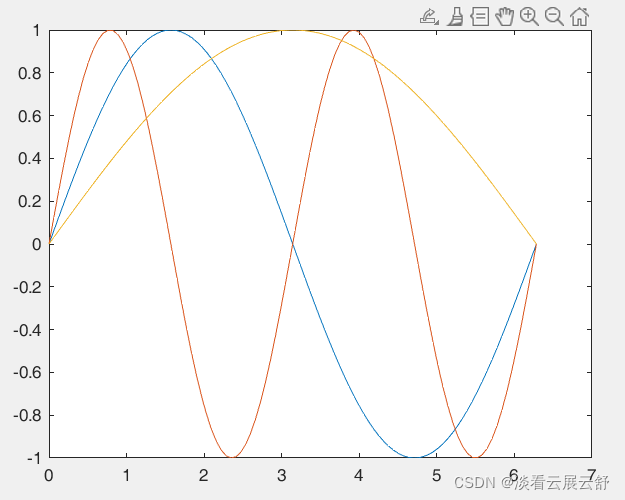
【绘制sinx,sin(2x),sin(x/2)的函数曲线】
>> x=linspace(0,2*pi,100); >> y=[sin(x);sin(2*x);sin(0.5*x)]; >> plot(x,y)
x,y为同型矩阵,以x、y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
>> t=0:0.01:2*pi; >> t1=t'; >> x=[t1,t1,t1]; >> y=[sin(t1),sin(2*t1),sin(0.5*t1)]; >> plot(x,y)
(4)含多个输入参数的plot函数
plot(x1,x2,x3```,xn,yn)
每一向量对构成一组数据点的横、纵坐标,绘制一条曲线
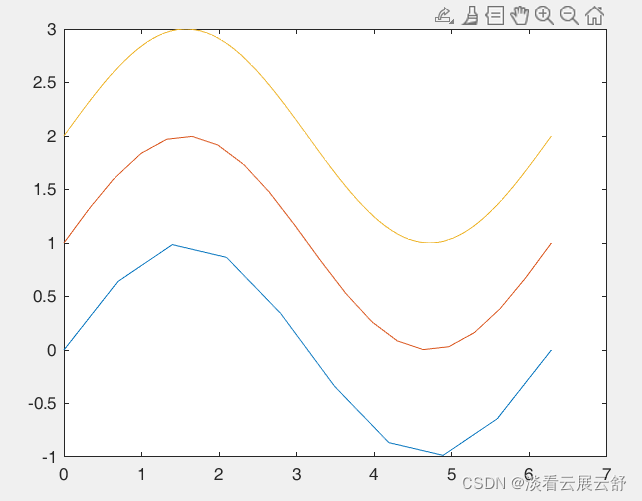
【采用不同个数的数据点绘制正弦函数曲线,观察曲线形态】
>> t1=linspace(0,2*pi,10); >> t2=linspace(0,2*pi,20); >> t3=linspace(0,2*pi,100); >> plot(t1,sin(t1),t2,sin(t2)+1,t3,sin(t3)+2)
点越多,图形越平滑
( 5)含选项的plot函数
plot(x,y,选项)
线型:“-":实线
":":虚线
"-.":点画线
"--":双画线
颜色,
"r":红
"g":绿
"b":蓝
"w":白
"k":黑色
数据点标记
"*":星号
"o":圆圈
"s":方块
"p":五角星
"^":朝上的三角符号
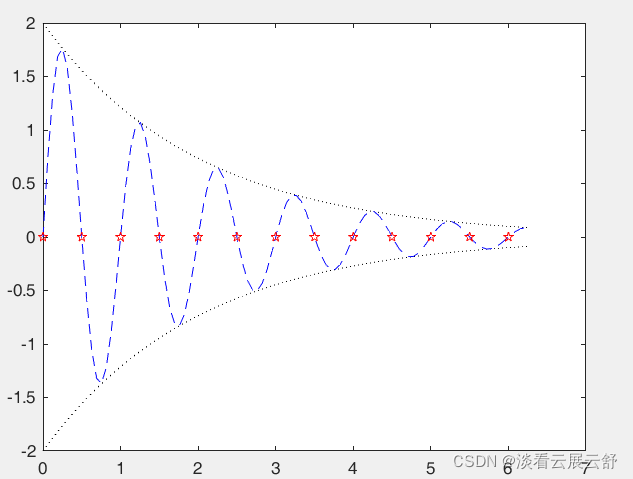
>> x=(0:pi/50:2*pi); >> x=(0:pi/50:2*pi)'; >> y1=2*exp(-0.5*x)*[1,-1]; >> y2=2*exp(-0.5*x).*sin(2*pi*x); >> x1=0:0.5:6; >> y3=2*exp(-0.5*x1).*sin(2*pi*x1); >> plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp')
>> y3=2*exp(-0.5*x1).*sin(2*pi*x1);
这里用'.*',代表两同型矩阵对应位置上的乘积,用'*'表述矩阵相乘
三、fplot函数
提出为解决:x的变化趋势未知。不同区间,函数图象差别大。如果自变量取值不合理,图像无法反映趋势。
1.fplot函数的调用
fplot(f,lims,选项)
f,代表一个函数,通常采用函数句柄的形式。
lims为x轴的取值范围,用二元向量[xmin,xmax]描述,默认值为[-5,5]。选项定义与plot函数相同
采用fplot函数绘制函数sin(1/x):
>> fplot(@(x)sin(1./x),[0,0.2],'b')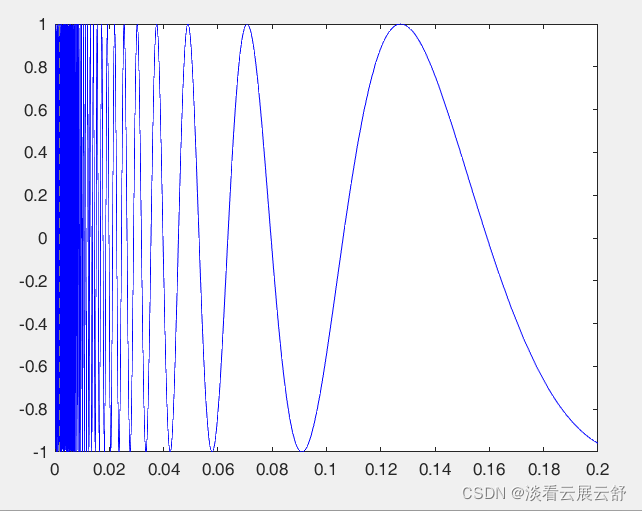
>> fplot(@(x)sin(1./x),[0,0.2],'b'),这里sin(1./x)此仍为一个向量,每个元素取了倒数。
数值与矩阵相除,如果数值在前,只能用./
(2)双输入函数参数的用法:
fplot(funx,funy,tlims,选项)
funx、funy代表函数,通常采用函数句柄
tlims为参数函数funx和funy的自变量的取值范围,用二元向量[tmin,tmax]描述
已知螺旋线的参数方程,绘制曲线
x=t*sint,y=t*cost
>> fplot(@(t)t.*sin(t),@(t)t.*cos(t),[0,10*pi],'r')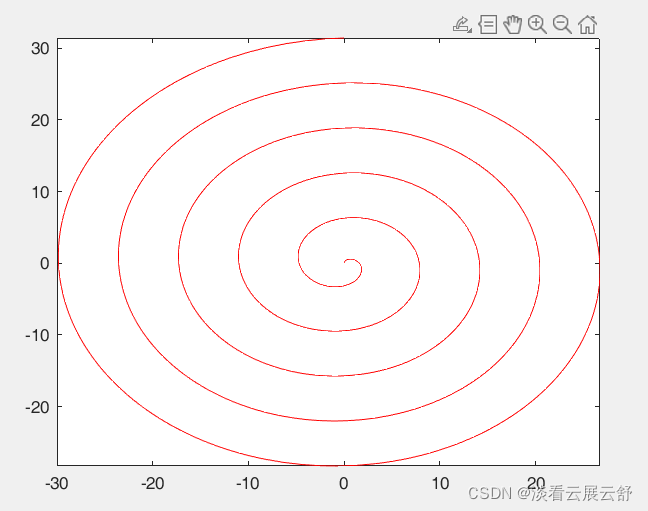
总结
plot与fplot的函数调用,注意点乘和点除,都是矩阵对应元素的相乘与相除