力扣435.无重叠区间----贪心策略三法(一暴力贪心,一优化验证过程,一另辟蹊径反面思考)
435. 无重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
题解:
对于此题,只要以一种贪心的视角取看待即可。
首先由于给的数组是乱序的,所以不妨先将其排下序再进行计算。
那么是按每个数组的start值大小排序还是按照end值大小排序呢?
首先我们要明白,秉着贪心的原则,我们为了尽可能的去少删,故我们删去的应该是其end值较大的。
因为在以一个区间为基准,找到n个区间重合时时,我们必定要删去n-1个区间,只留下一个区间,而为了使留下的这个区间尽可能的不要再和别的区间“沾上关系”,故选择end值小的留下。
且在经过排序后,我们从第一个元素开始已经是end最小的了,所以只要发现与此元素的区间有重合的就直接删去即可,因为若留下end大的可能不只与该元素区间重合,可能还与别的区间重合。
可由一图加深理解:
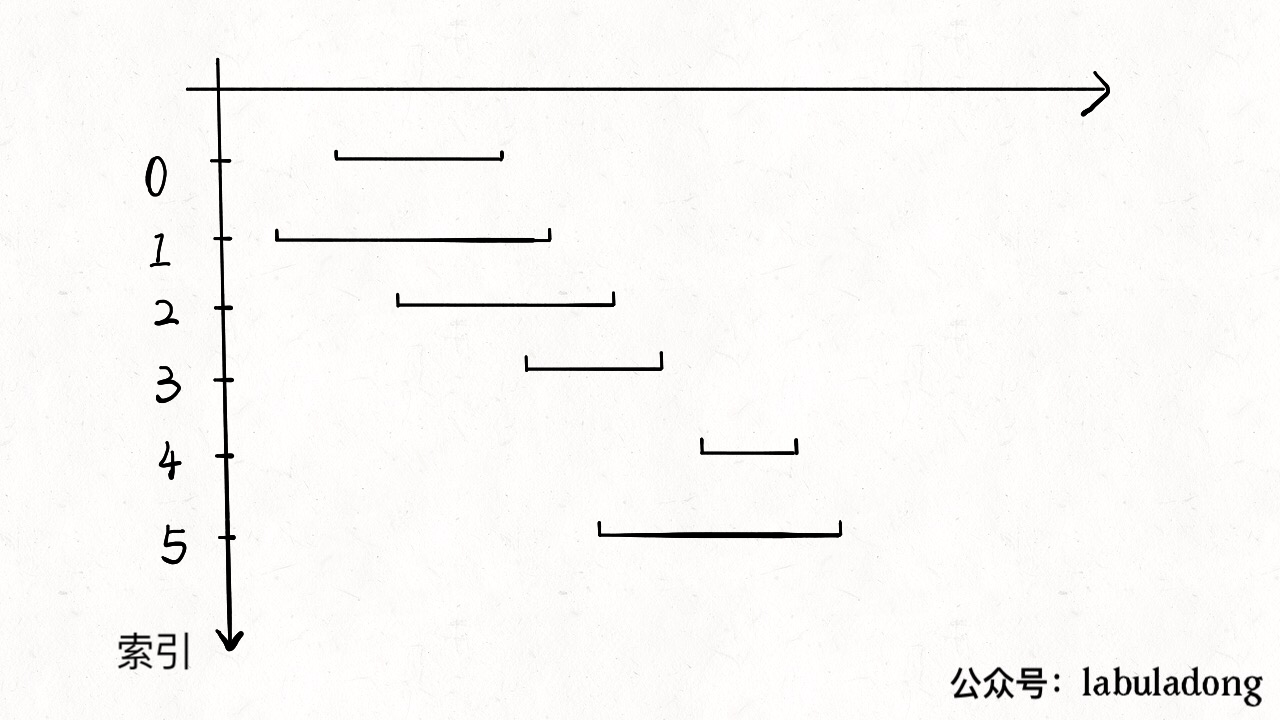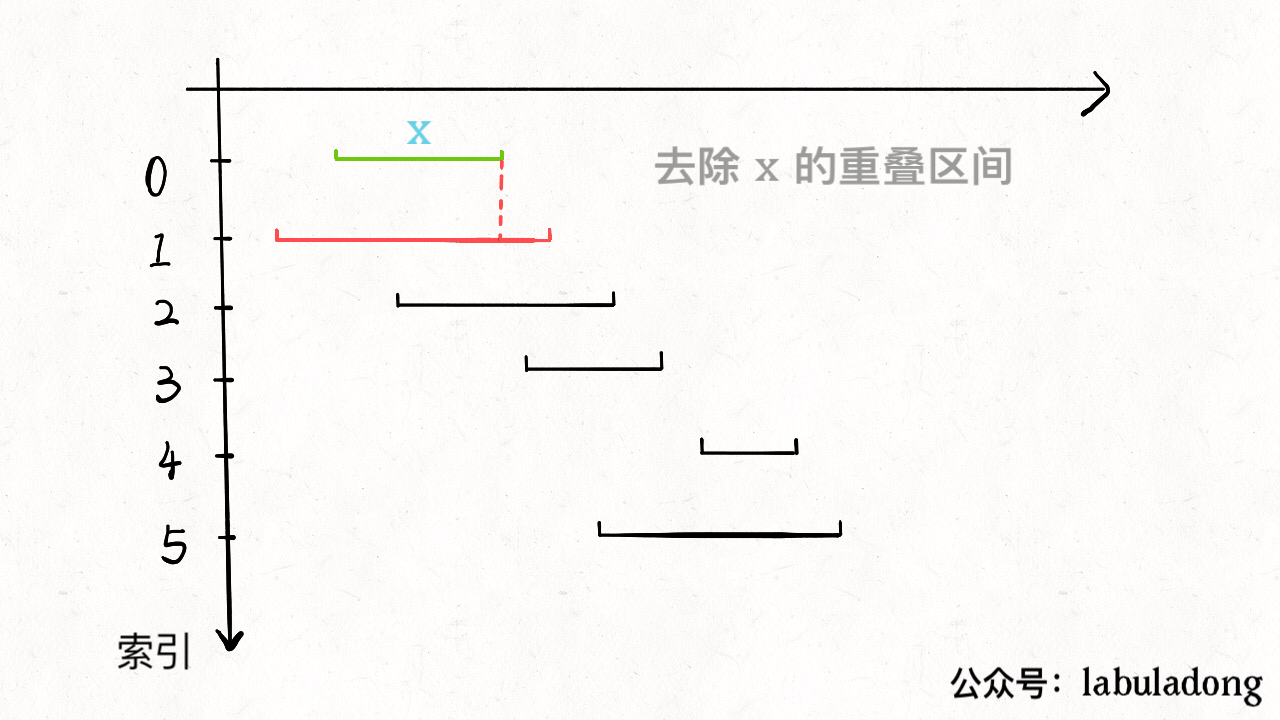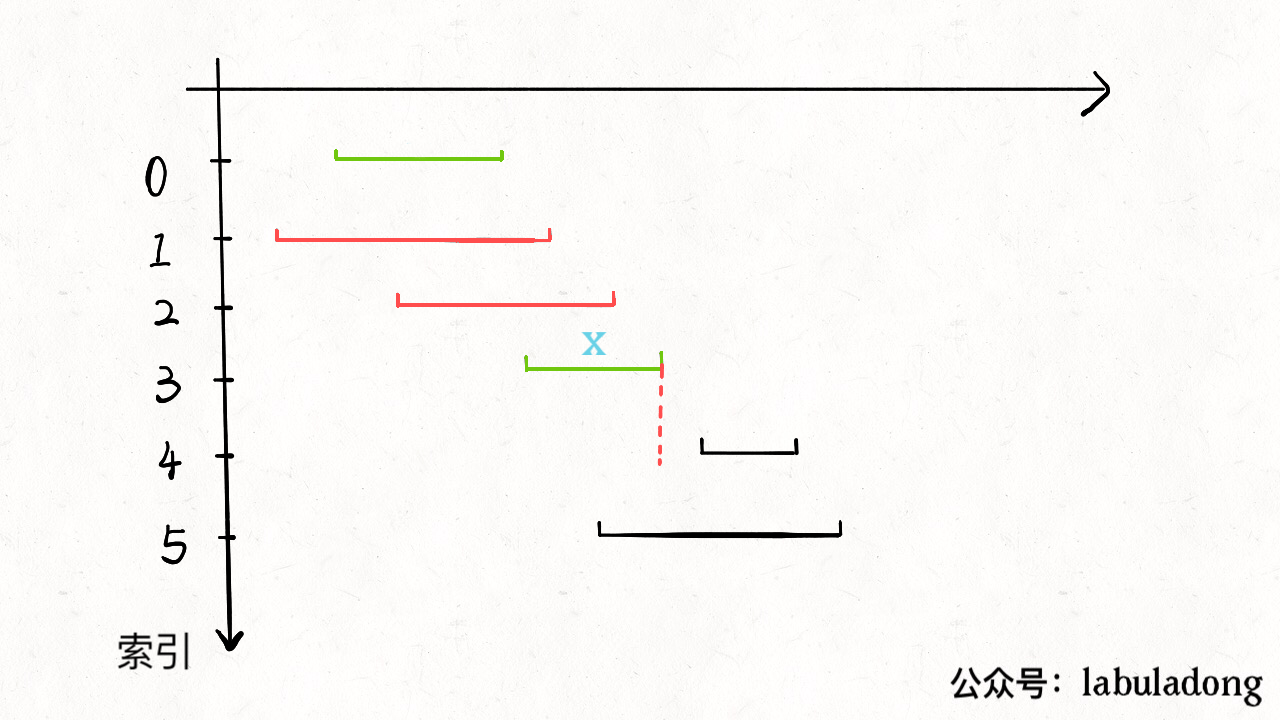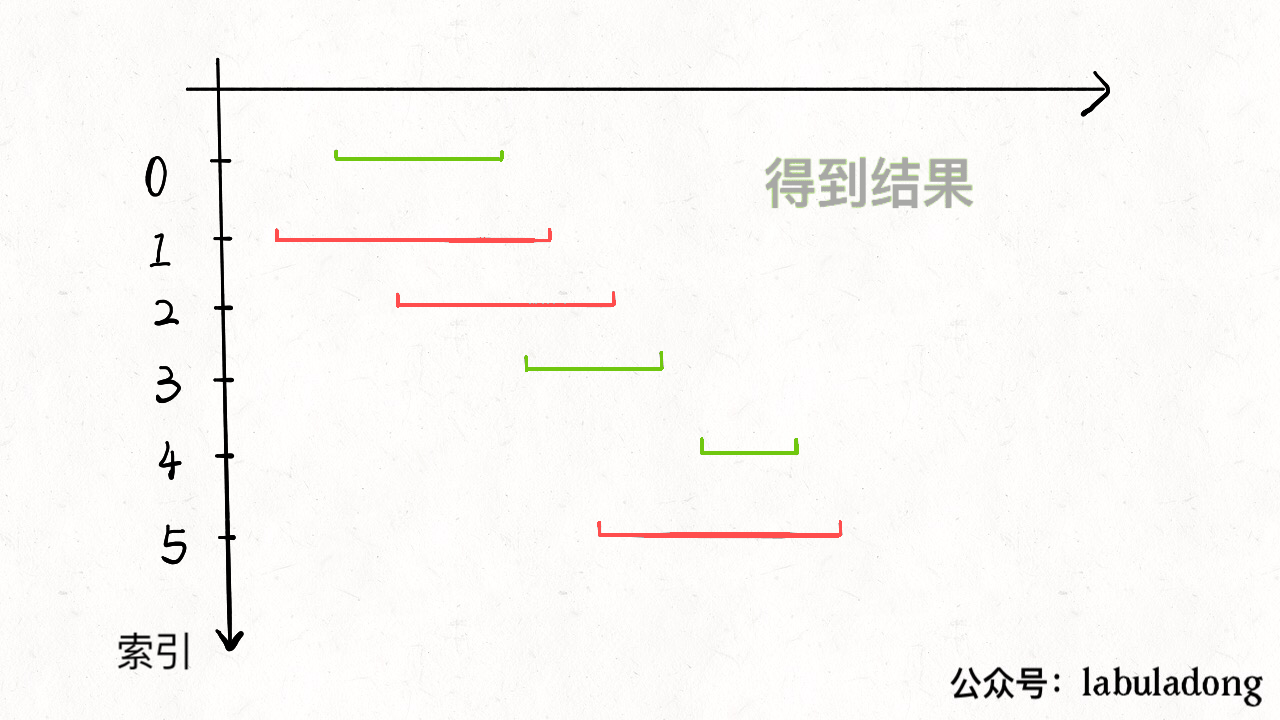
图片来源:labuladong的算法小抄
因此下面是我第一次写出的代码,而我开始没有恰当考虑怎样去验证两个区间是重合的,因此代码较为繁杂,效率较低,且我着重于直接找到要删去的区间。
-------------注:下面的right相当于我原先提到的end,left相当于我原先提到的start
代码:
int cmp(void*_x,void*_y)
{
int *x=*(int**)_x;
int *y=*(int**)_y;
return x[1]>y[1];
}
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize){
if(intervalsSize==0)
return 0;
int sum = 0;//储存要删去的区间数目
qsort(intervals,intervalsSize,sizeof(int*),cmp);//不排序会误删
for(int i=0;i<intervalsSize;i++)//遍历一遍数组,即将每个数组都当成“基准”试一试
{
if(intervals[i][0]==INT_MAX)//由下面可知此代表“删去”,所以“删去”的不用进行循环了
continue;
for(int j=0;j<intervalsSize;j++)//在进行一次循环找是否有重合的区间
{
if(i==j||intervals[j][0]==INT_MAX)//已经“删去”的和下标一样的不用进行循环了
continue;
if((intervals[j][0]>=intervals[i][0]&&intervals[j][0]<intervals[i][1])||(intervals[j][1]>intervals[i][0]&&intervals[j][1]<=intervals[i][1]))//此为重合的条件,也是此代码繁杂之处
{
if(intervals[j][1]>intervals[i][1])//比较end
{
sum++;
intervals[j][1]=INT_MAX;//此代表“删去”的意思,因为c语言不能严格的执行删除操作
intervals[j][0]=INT_MAX;//所以我们把这个区间变成无穷远即可代表他是被删去了
continue;
}
else
{
sum++;
intervals[i][1]=INT_MAX;//“删去”基准
intervals[i][0]=INT_MAX;
break;//若基准被“删去”了,则直接跳出循环进行下次即可,因为基准已经没了
}
}
}
}
return sum;
}

后来由以前的“打气球问题”想到可以对重合区间的验证过程进行优化,
即要验证两个区间是否重合,因为我们已经按照end值排好序了,若作为基准区间的下一个区间其start值大于等于基准区间的end则一定不重合,若其start小于基准区间的end一定重合,这恰恰是因为我们已经按照end大小排好序了,所以基准区间的下一个区间的end必定是大于基准区间的end的。
所以把此验证过程转化到只比较下一个的start和基准的end即可。
于是写出了以下代码:
-------(注意的是,因为我们已经按照end排好序了,所以基准区间就从第一个开始即可,因为他必然是end最小的)。
int cmp(void*_x,void*_y)
{
int *x=*(int**)_x;
int *y=*(int**)_y;
return x[1]>y[1];
}
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize){
if(intervalsSize==0)
return 0;
int sum = 0;//储存要删去的区间数目
qsort(intervals,intervalsSize,sizeof(int*),cmp);//不排序会误删
for(int i=0;i+1<intervalsSize;i++)//遍历一遍数组,即将每个数组都当成“基准”试一试
{
if(intervals[i][1]==INT_MAX)//此为已经“删去”了,所以不用参与循环了
continue;
int right = intervals[i][1];//先储存基准区间的end
int j = i+1;//不能改变i,所以设了j来完成接下来的循环找重合区间任务
while(intervals[j][0]<right)
{
sum++;
intervals[j][0]=INT_MAX;//"删除"操作
intervals[j][1]=INT_MAX;
j++;
if(j==intervalsSize)//防止越界,所以跳出来
break;
}
}
return sum;
}

但两种方法都是着重于直接找应删去的区间数,其实可以另辟蹊径,从反面来思考。
即总区间数量我们已经知道了,我们只要求出不重合的区间数,那么二者相减即为所求。
不明白代码内改变基准位置的作用的话可以再看一下前面的图。
优化后如下:
int cmp(void*_x,void*_y)
{
int *x=*(int**)_x;
int *y=*(int**)_y;
return x[1]>y[1];
}
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize){
if(intervalsSize==0||intervalsSize==1)
return 0;
int sum = 1;//先储存一下不重合的区间,因为在区间总数大于1的情况下,不重合区间最少要有一个,因为我们是n个删掉n-1个
qsort(intervals,intervalsSize,sizeof(int*),cmp);//不排序会误删
int right=intervals[0][1];//将基准的end先储存起来
for(int i=1;i<intervalsSize;i++)
{
if(intervals[i][0]>=right)//在以一个位置为基准的情况下找到了一个不与基准重合的区间,就要改变一下基准位置了
{
sum++;//证明多了个不重合的区间
right=intervals[i][1];//改变“基准”的end值
}
}
return intervalsSize-sum;
}
