【计算机图形学 】扫描线多边形填充算法 | OpenGL+鼠标交互

其他计算机图形学实验

传送门

前言

实现多边形扫描线填充算法，并和鼠标进行交互。
具体原理略过，会贴上完整代码，可直接运行。

环境：
vs2019,OpenGL的库（可以搜索如何用vs使用OpenGL的库，可以使用vs自带的插件或者其他方法，很方便）

要点：
1.NET和AET的创建，改动
2.改变鼠标点击和鼠标拖拽的响应事件。

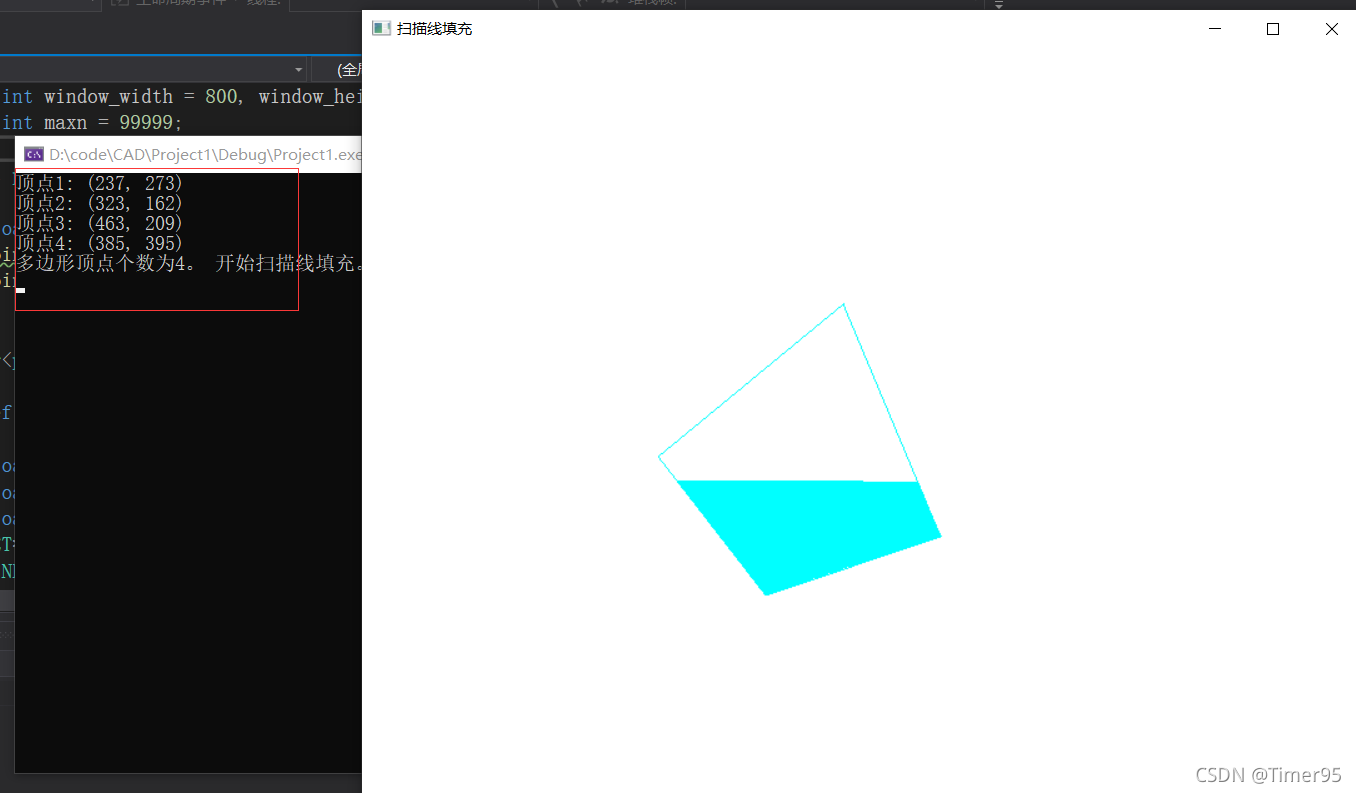
最终效果：
用鼠标随意画顶点，然后展示填充过程
对应控制台会输出顶点坐标和个数

思路借鉴

文章1
文章2

步骤

1.点的结构体

struct point
{
	float x, y;
	point(){}
	point(int xx, int yy):
		x(xx), y(yy) {}
};
vector<point> vertice; //顶点

2. AET 活性边表、NET新边表 的结构体

typedef struct XET
{
	float x;
	float dx;  // 从当前扫描线到下一条扫描线间x的增量，即斜率的倒数
	float ymax; //该边所交的最高扫描线的坐标值ymax
	XET* next;
}AET, NET; //AET 活性边表； NET新边表

3. 扫描线算法实现

void PolyScan()
{
	/*得到最高点的y坐标*/
	int Max_Y = 0;
	for (int i = 0; i < vertice.size(); i++) 
		/*Max_Y = max(Max_Y, vertice[i].y);*/
		if (vertice[i].y > Max_Y)
			Max_Y = vertice[i].y;


	//初始化AET表
	AET* pAET = new AET;
	pAET->next = NULL;

	//初始化NET表
	NET* pNET[800]; //吊桶
	for (int i = 0; i <= Max_Y; i++)
	{
		pNET[i] = new NET;
		pNET[i]->next = NULL;;
	}

	//扫描并且建立NET表
	int len = vertice.size(); //顶点个数
	for (int i = 0; i <= Max_Y; i++)
	{
		for (int j = 0; j < len; j++) //扫描每个点
		{
			if (i == vertice[j].y)
			{
				//如果一个点和前一个点有一条边相连，则该点和后面一个点也相连
				//！这个式子 便于最后一个顶点和第一个点相连 和 防止出现负数
				
				//判断当前点的高低，使ymax、DX、DY的计算有变化
				if (vertice[(j - 1 + len) % len].y > vertice[j].y)
				{
					//前一个点在当前点的上方
					NET* p = new NET;
					p->x = vertice[j].x;
					p->ymax = vertice[(j - 1 + len) % len].y;//与当前扫描线相交的活性边 的 最高点即为相邻顶点的y
					float DX = vertice[(j - 1 + len) % len].x - vertice[j].x;
					float DY = vertice[(j - 1 + len) % len].y - vertice[j].y;
					p->dx = DX / DY;//dx为直线斜率的倒数
					p->next = pNET[i]->next;
					pNET[i]->next = p;
				}
				if (vertice[(j + 1) % len].y > vertice[j].y)
				{
					//后一个点在当前点的上方
					NET* p = new NET;
					p->x = vertice[j].x;
					p->ymax = vertice[(j + 1) % len].y;
					float DX = vertice[(j + 1) % len].x - vertice[j].x;
					float DY = vertice[(j + 1) % len].y - vertice[j].y;
					p->dx = DX / DY;//dx为直线斜率的倒数
					p->next = pNET[i]->next;
					pNET[i]->next = p;
				}
			}
		}
	}

	//建立并且更新活性边表AET
	//各条扫描线i
	for (int i = 0; i <= Max_Y; i++)
	{
		/*把新边表NET[i] 中的边结点用插入排序法插入AET表，使之按x坐标递增顺序排列*/
		
		//计算每条扫描线上不同线产生的新的交点x，更新AET
		NET* p = pAET->next;
		while (p)
		{
			p->x = p->x + p->dx; //更新x坐标
			p = p->next;
		}

		//断表排序,不再开辟空间 
		AET* tq = pAET;
		p = pAET->next;
		tq->next = NULL;
		while (p)//顺着链表往下走
		{
			//找到第一个比它大的数字tq->next->next->x，则从p->next到tq->next都是比p->x小的
			while (tq->next != NULL && tq->next->x <= p->x)
				tq = tq->next;
			//插入p到tq和tq->next之间
			NET* t = p->next;
			p->next = tq->next;
			tq->next = p;
			p = t;

			tq = pAET;//回到头
		}

		/*(改进算法) 取消求交，减少计算量*/
		//先从AET表中删除ymax==i的结点****************************************/
		//像素的取舍问题，保证多边形的“下闭上开”，避免填充扩大化（交点的个数应保证为偶数个）
		AET* q = pAET;
		p = q->next;
		while (p)
		{
			if (p->ymax == i)
			{
				q->next = p->next;
				delete p;
				p = q->next;
			}
			else
			{
				q = q->next;
				p = q->next;
			}
		}

		//若NET中有新点，将其用插入法插入AET，按x递增的顺序排列
		p = pNET[i]->next;
		q = pAET;
		while (p)
		{
			while (q->next && p->x >= q->next->x)
				q = q->next;
			//插入p
			NET* t = p->next;
			p->next = q->next;
			q->next = p;
			p = t;

			q = pAET;//回到头
		}

		//配对后填充颜色
		p = pAET->next;
		while (p && p->next != NULL)
		{
			for (float j = p->x; j <= p->next->x; j++)
			{
				//扫描线画点
				draw_a_point(j, i);
				//cout << "(" << j << ", " << i << ")" << endl;
			}
			p = p->next->next;//考虑端点情况
		}
	}
	glFlush();
}

4. 改变鼠标响应函数

void mymouse(int button, int state, int x, int y)
{
	//左键
	if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN)
	{
		draw_a_point(x, window_height - y);

		point p(x, window_height - y);
		vertice.push_back(p);
		cout << "顶点" << vertice.size() << ": (" << x << ", " << window_height - y << ")" << endl;
	}
	//右键
	if (button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN)
	{
		glClearColor(1, 1, 1, 1);//设置绘制窗口颜色为白色
		glColor3f(0, 1, 1);

		//绘制多边形
		glBegin(GL_LINES);	
		for (int i = 0; i < vertice.size(); i++)
		{
			if (i == vertice.size() - 1)//画完最后一个点，使其闭合
			{
				glVertex2f(vertice[0].x, vertice[0].y);
				glVertex2f(vertice[i].x, vertice[i].y);
			}
			else
			{
				glVertex2f(vertice[i].x, vertice[i].y);
				glVertex2f(vertice[i + 1].x, vertice[i + 1].y);
			}
		}
		glEnd();
		glFlush();
	}

	//鼠标中间
	if (button == GLUT_MIDDLE_BUTTON && state == GLUT_DOWN)
	{
		//cout << "center: (" << x << ", " << y << ")" << endl;
		//BoundaryFill4(x, window_height - y);
		//BoundaryFill4_Stack(x, window_height - y);

		cout << "多边形顶点个数为" << vertice.size() << "。 " << "开始扫描线填充。" << endl;
		PolyScan();
	}
}

完整代码

//扫描线算法
#include<iostream>
#include<gl/glut.h>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
const int window_width = 800, window_height = 600;
const int maxn = 99999;

struct point
{
	float x, y;
	point(){}
	point(int xx, int yy):
		x(xx), y(yy) {}
};
vector<point> vertice; //顶点

typedef struct XET
{
	float x;
	float dx;  // 从当前扫描线到下一条扫描线间x的增量，即斜率的倒数
	float ymax; //该边所交的最高扫描线的坐标值ymax
	XET* next;
}AET, NET; //AET 活性边表； NET新边表

void draw_a_point(int x, int y);
void PolyScan();
void mymouse(int button, int state, int x, int y);
void display();


int main(int argc, char* argv[])
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowPosition(100, 50);
	glutInitWindowSize(window_width, window_height);
	glutCreateWindow("扫描线填充");

	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0, window_width, 0, window_height);

	glClearColor(1, 1, 1, 1);
	glClear(GL_COLOR_BUFFER_BIT);

	glutMouseFunc(&mymouse);
	glutDisplayFunc(&display);

	glutMainLoop();
	return 0;
}

//画点函数
void draw_a_point(int x, int y)
{
	glBegin(GL_POINTS);
	glColor3f(0, 1, 1);
	glVertex2f(x, y);
	glEnd();
	glFlush();
}

void PolyScan()
{
	/*得到最高点的y坐标*/
	int Max_Y = 0;
	for (int i = 0; i < vertice.size(); i++) 
		/*Max_Y = max(Max_Y, vertice[i].y);*/
		if (vertice[i].y > Max_Y)
			Max_Y = vertice[i].y;


	//初始化AET表
	AET* pAET = new AET;
	pAET->next = NULL;

	//初始化NET表
	NET* pNET[800]; //吊桶
	for (int i = 0; i <= Max_Y; i++)
	{
		pNET[i] = new NET;
		pNET[i]->next = NULL;;
	}

	//扫描并且建立NET表
	int len = vertice.size(); //顶点个数
	for (int i = 0; i <= Max_Y; i++)
	{
		for (int j = 0; j < len; j++) //扫描每个点
		{
			if (i == vertice[j].y)
			{
				//如果一个点和前一个点有一条边相连，则该点和后面一个点也相连
				//！这个式子 便于最后一个顶点和第一个点相连 和 防止出现负数
				
				//判断当前点的高低，使ymax、DX、DY的计算有变化
				if (vertice[(j - 1 + len) % len].y > vertice[j].y)
				{
					//前一个点在当前点的上方
					NET* p = new NET;
					p->x = vertice[j].x;
					p->ymax = vertice[(j - 1 + len) % len].y;//与当前扫描线相交的活性边 的 最高点即为相邻顶点的y
					float DX = vertice[(j - 1 + len) % len].x - vertice[j].x;
					float DY = vertice[(j - 1 + len) % len].y - vertice[j].y;
					p->dx = DX / DY;//dx为直线斜率的倒数
					p->next = pNET[i]->next;
					pNET[i]->next = p;
				}
				if (vertice[(j + 1) % len].y > vertice[j].y)
				{
					//后一个点在当前点的上方
					NET* p = new NET;
					p->x = vertice[j].x;
					p->ymax = vertice[(j + 1) % len].y;
					float DX = vertice[(j + 1) % len].x - vertice[j].x;
					float DY = vertice[(j + 1) % len].y - vertice[j].y;
					p->dx = DX / DY;//dx为直线斜率的倒数
					p->next = pNET[i]->next;
					pNET[i]->next = p;
				}
			}
		}
	}

	//建立并且更新活性边表AET
	//各条扫描线i
	for (int i = 0; i <= Max_Y; i++)
	{
		/*把新边表NET[i] 中的边结点用插入排序法插入AET表，使之按x坐标递增顺序排列*/
		
		//计算每条扫描线上不同线产生的新的交点x，更新AET
		NET* p = pAET->next;
		while (p)
		{
			p->x = p->x + p->dx; //更新x坐标
			p = p->next;
		}

		//断表排序,不再开辟空间 
		AET* tq = pAET;
		p = pAET->next;
		tq->next = NULL;
		while (p)//顺着链表往下走
		{
			//找到第一个比它大的数字tq->next->next->x，则从p->next到tq->next都是比p->x小的
			while (tq->next != NULL && tq->next->x <= p->x)
				tq = tq->next;
			//插入p到tq和tq->next之间
			NET* t = p->next;
			p->next = tq->next;
			tq->next = p;
			p = t;

			tq = pAET;//回到头
		}

		/*(改进算法) 取消求交，减少计算量*/
		//先从AET表中删除ymax==i的结点****************************************/
		//像素的取舍问题，保证多边形的“下闭上开”，避免填充扩大化（交点的个数应保证为偶数个）
		AET* q = pAET;
		p = q->next;
		while (p)
		{
			if (p->ymax == i)
			{
				q->next = p->next;
				delete p;
				p = q->next;
			}
			else
			{
				q = q->next;
				p = q->next;
			}
		}

		//若NET中有新点，将其用插入法插入AET，按x递增的顺序排列
		p = pNET[i]->next;
		q = pAET;
		while (p)
		{
			while (q->next && p->x >= q->next->x)
				q = q->next;
			//插入p
			NET* t = p->next;
			p->next = q->next;
			q->next = p;
			p = t;

			q = pAET;//回到头
		}

		//配对后填充颜色
		p = pAET->next;
		while (p && p->next != NULL)
		{
			for (float j = p->x; j <= p->next->x; j++)
			{
				//扫描线画点
				draw_a_point(j, i);
				//cout << "(" << j << ", " << i << ")" << endl;
			}
			p = p->next->next;//考虑端点情况
		}
	}
	glFlush();
}
void mymouse(int button, int state, int x, int y)
{
	//左键
	if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN)
	{
		draw_a_point(x, window_height - y);

		point p(x, window_height - y);
		vertice.push_back(p);
		cout << "顶点" << vertice.size() << ": (" << x << ", " << window_height - y << ")" << endl;
	}
	//右键
	if (button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN)
	{
		glClearColor(1, 1, 1, 1);//设置绘制窗口颜色为白色
		glColor3f(0, 1, 1);

		//绘制多边形
		glBegin(GL_LINES);	
		for (int i = 0; i < vertice.size(); i++)
		{
			if (i == vertice.size() - 1)//画完最后一个点，使其闭合
			{
				glVertex2f(vertice[0].x, vertice[0].y);
				glVertex2f(vertice[i].x, vertice[i].y);
			}
			else
			{
				glVertex2f(vertice[i].x, vertice[i].y);
				glVertex2f(vertice[i + 1].x, vertice[i + 1].y);
			}
		}
		glEnd();
		glFlush();
	}

	//鼠标中间
	if (button == GLUT_MIDDLE_BUTTON && state == GLUT_DOWN)
	{
		//cout << "center: (" << x << ", " << y << ")" << endl;
		//BoundaryFill4(x, window_height - y);
		//BoundaryFill4_Stack(x, window_height - y);

		cout << "多边形顶点个数为" << vertice.size() << "。 " << "开始扫描线填充。" << endl;
		PolyScan();
	}
}
void display()
{
	glClear(GL_COLOR_BUFFER_BIT);
	glColor3f(0.0, 0.4, 0.2);
	glPointSize(1);
	glBegin(GL_POINTS);
	PolyScan();
	glEnd();
	glFlush();
}

总结

扫描线算法部分，建立NET 和 建立并且更新活性边表AET 这两个地方比较复杂，可以带入图中多想