C语言数据结构学习（clion版本）

栈的应用（就近匹配，逆波兰表达式）

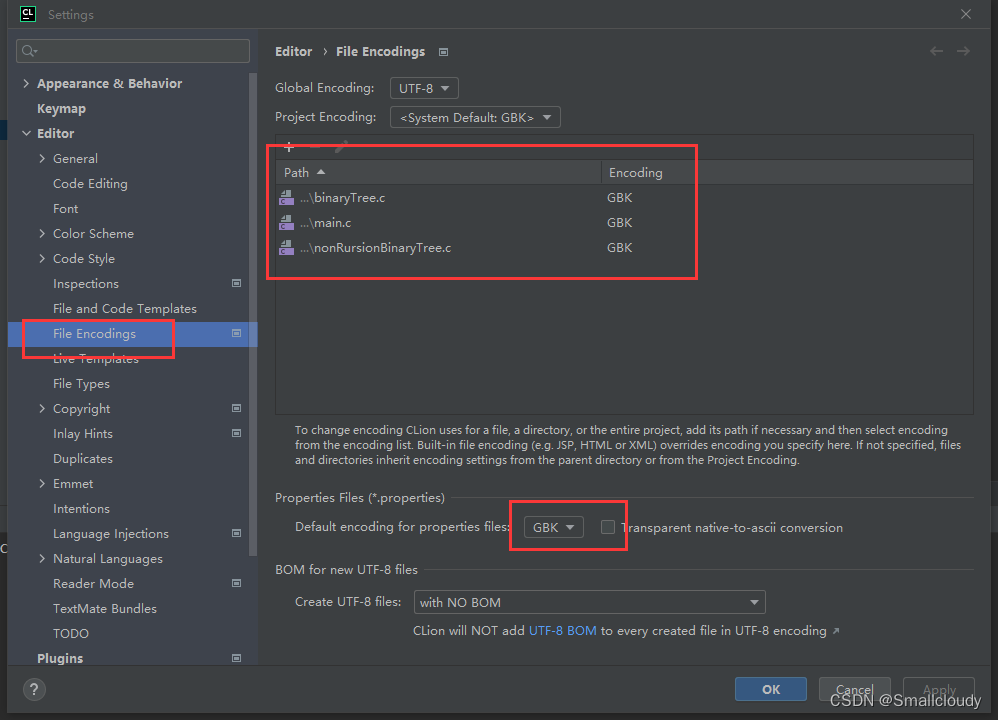
先放一张clion设置截图，用于分割不同作用的文件，以及怎么定义路径和引用。

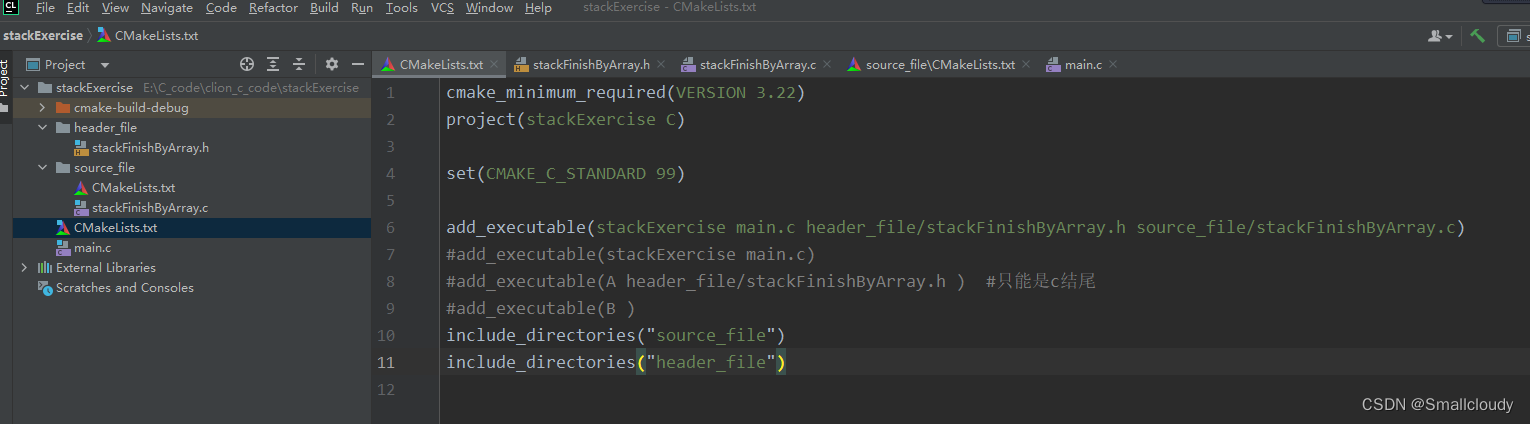
需要在main.c同级的CMakeLists.txt中定义source_file和header_file。
在CMakeLists.txt加入设置：

include_directories("source_file")
include_directories("header_file")

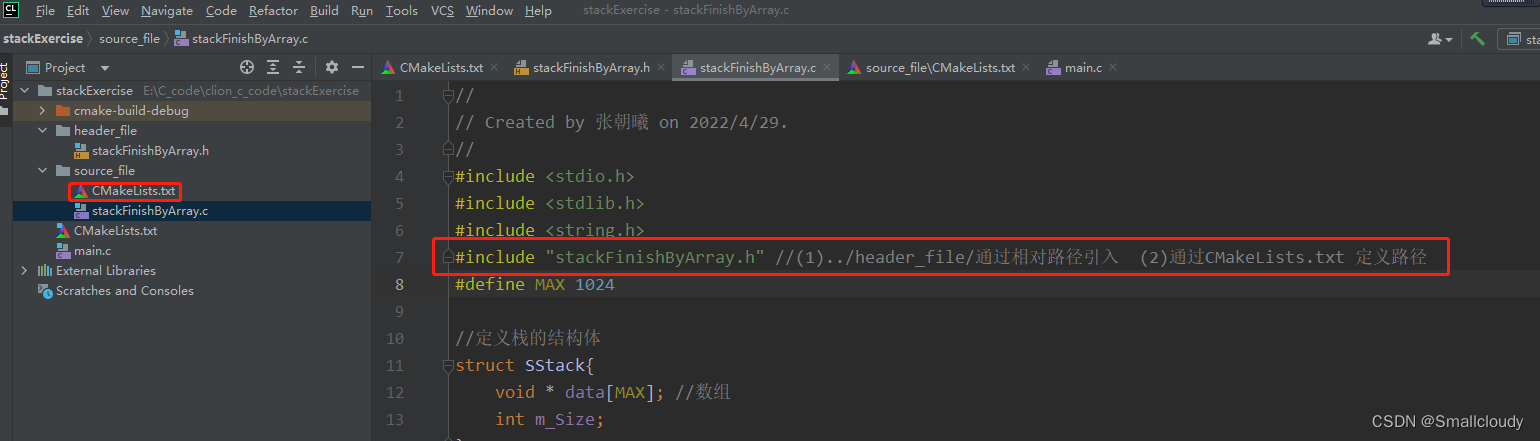
在source_file中对header_file中的文件进行实现，在头文件那里，可以通过相对路径引入，也可以通过CMakeLists.txt文件，设置。

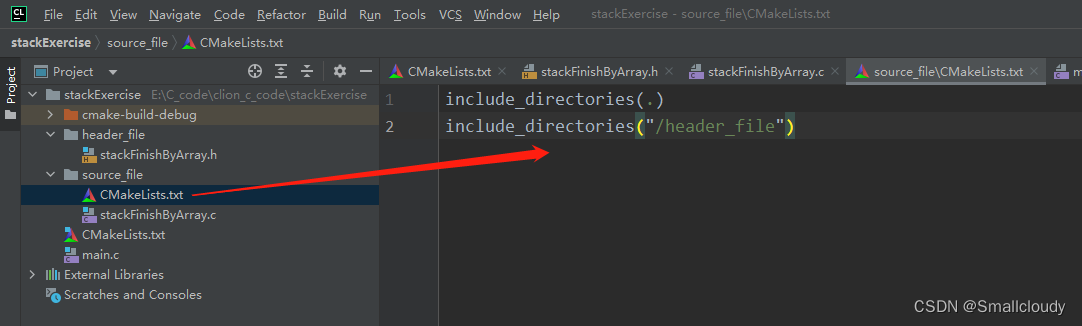
这样就让clion中的C语言工程和visual studio中的一样了。注意，clion中，尽量不要用中文定义文件夹，容易出现路径寻找不到的问题。

括号匹配

#include <stdio.h>
#include "stackFinishByArray.h"

int isLeft(char ch){
   return ch=='(';
}

int isRight(char ch){
    return ch==')';
}

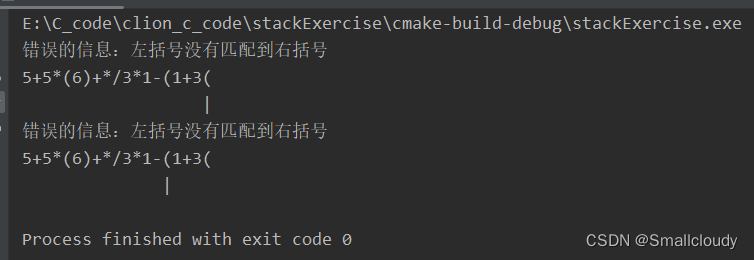
void printError(char *str,char *errMsg,const char *pos){
    printf("错误的信息：%s\n",errMsg);
    printf("%s\n",str);

    //计算打印空格的数量
    long long num = pos-str; //char型指针地址（占一个字节）相减
    for (int i = 0; i < num; ++i) {
        printf(" ");
    }
    printf("|\n");
}
void test01()
{
    char *str = "5+5*(6)+*/3*1-(1+3(";
    char *p =str;   //定义一个指针指向字符串的头地址
    seqStack myStack = init_Stack();
    while (*p!='\0'){ //没有到字符串的终止符的时候

        //判断是不是左括号
        if(isLeft(*p)){ //
            push_SeqStack(myStack,p);
        }

        //判断是不是右括号
        if(isRight(*p)){
            if(size_SeqStack(myStack)>0){  //栈不为空，弹出栈
                pop_SeqStack(myStack);
            } else{  //栈为空，直接报错，打印错误信息
                printError(str,"右括号没有匹配到左括号",p);
                break;
            }
        }
        p++;
    }

    //判断是否为空栈
    while (size_SeqStack(myStack)>0){

        printError(str,"左括号没有匹配到右括号", top_SeqStack(myStack));
        pop_SeqStack(myStack);
    }

}
int main() {
    test01();
    //printf("Hello, World!\n");
    return 0;
}

中缀转后缀表达式

算法流程

中缀表达式 转后缀表达式

可以利用自己已经实现的栈

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//#define MAX 1024
//
定义栈的结构体
//struct SStack{
//    void * data[MAX]; //数组
//    int m_Size;
//};

typedef void* seqStack;
//开始编写stack的接口

//初始化栈
seqStack init_Stack();

//入栈
void push_SeqStack(seqStack stack,void * data);

//出栈
void pop_SeqStack(seqStack stack);
//获取栈顶元素
void* top_SeqStack(seqStack stack);

//返回栈大小
int size_SeqStack(seqStack stack);

//判断栈是否为空(0为空，1非空)
int isEmpty(seqStack stack);


//销毁栈
void destroy_SeqStack(seqStack stack);

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "stackFinishByArray.h" //(1)../header_file/通过相对路径引入  (2)通过CMakeLists.txt 定义路径
#define MAX 1024

//定义栈的结构体
struct SStack{
    void * data[MAX]; //数组
    int m_Size;
};

typedef void* seqStack;
//开始编写stack的接口

//初始化栈
seqStack init_Stack(){

    struct SStack *myStack=malloc(sizeof (struct SStack)); //先给管理栈的结构体开辟空间
    if(myStack==NULL){
        return NULL;
    }

    //清空数组中的每个元素
    memset(myStack->data,0, sizeof(void*)*MAX); //将数组中的每个元素赋值为0

    myStack->m_Size=0;

    return myStack;
}

//入栈
void push_SeqStack(seqStack stack,void * data){
    if(stack==NULL){
        return;
    }

    //判断栈是否已经满了，如果满了，不能入栈
    struct SStack *myStack = stack;
    if(myStack->m_Size==MAX){
        return;
    }

    myStack->data[myStack->m_Size]=data; //入栈插入
    myStack->m_Size++; //更新栈大小
}

//出栈
void pop_SeqStack(seqStack stack){
    if(stack==NULL){
        return ;
    }

    //如果是空栈，不执行出栈
    struct SStack *myStack = stack;
    if(myStack->m_Size==0){
        return ;
    }

//    void *data = myStack->data[myStack->m_Size-1];
//    memset(myStack->data[myStack->m_Size-1],0,sizeof(void *));
    myStack->data[myStack->m_Size-1]=NULL;
    myStack->m_Size--;
}
//获取栈顶元素
void* top_SeqStack(seqStack stack){
    if(stack==NULL){
        return NULL;
    }

    struct SStack *myStack=stack;
    if(myStack->m_Size<=0){
        return NULL;
    }

    return myStack->data[myStack->m_Size-1];
}

//返回栈大小
int size_SeqStack(seqStack stack){
    if(stack==NULL){
        return -1;
    }

    struct SStack *myStack=stack;
    return myStack->m_Size;
}

//判断栈是否为空(0为空，1非空)
int isEmpty(seqStack stack){
    if(stack==NULL){
        return -1; //真
    }

    struct SStack *myStack=stack;
    if(myStack->m_Size<=0){
        return 1; //真
    } else{
        return 0; //假
    }
}

//销毁栈
void destroy_SeqStack(seqStack stack){
    if(stack==NULL){
        return;
    }

    free(stack);
    stack=NULL;
}

中缀转后缀是可以正常实现的，但是还有问题，就是对数字和字符的转换有问题，同时通过后缀去计算大表达式的值也有点问题，先记录在这里，有空来解一下bug。

#include <stdio.h>
#include "stackFinishByArray.h"

//我的这种写法不对//很多清空不符合（表达式中的数字提取就有问题）
//遍历后缀表达式计算结果
float calculate(seqStack stack, char *arr){
    if(arr ==NULL){
        return -1;
    }
    char *myArr = arr; //数组的首地址

    //开始入栈
    while (*myArr!='\0'){
        if(*myArr!='+' &&  *myArr!='-' &&  *myArr!='*' &&  *myArr!='/'){
            //这里就应该将其转化成数字，压入栈中
            push_SeqStack(stack,myArr);  //这样压入栈中的就全是数字了
            myArr++;
        } else{

            int element = size_SeqStack(stack);
            //弹出第一个数
            char *temp_first = top_SeqStack(stack); //这里由于是由数组实现，char *temp_first相当于指向了一个字符串，我们只需要提取首地址即可
            int first = *temp_first-'0';
            pop_SeqStack(stack);


            //弹出第二个数
            char *temp_second = top_SeqStack(stack);
            int second = *temp_second-'0';
            pop_SeqStack(stack);

            if(*myArr=='+'){
                int result = first + second;
                push_SeqStack(stack,&result);
                myArr++;
            } else if(*myArr=='-'){
                int result = second - first;
                push_SeqStack(stack,result);
                myArr++;
            } else if(*myArr=='*'){
                int result = second * first;
                push_SeqStack(stack,&result);
                myArr++;
            } else{
                float result = second / first;
                push_SeqStack(stack,&result);
                myArr++;
            }

        }
    }
    float *result = top_SeqStack(stack);
    return *result;
}
//利用返回值比较优先级
int priority(const char *ch){
    if(*ch=='*' || *ch=='/'){
        return 1;
    } else if(*ch=='+' || *ch=='-') {
        return 0;
    }
    return -1;
}
//中缀转后缀表达式
void test02(){

    char *str = "8+(3-1)*5"; //该表达式可以通过键盘输入
    seqStack myStack = init_Stack(); //初始化一个栈
    char temp[10];
    int index=0;
    char *pStr = str; //获取首元素地址
    while (*pStr!='\0'){

        if( *pStr!='+' && *pStr!='-' && *pStr!='*' && *pStr!='/' && *pStr!='(' && *pStr!=')'){
            temp[index++]=*pStr; //将数字交给字符数组存储
            pStr++;
            continue; //结束此次循环，进入下一次
        }
        if(*pStr=='('){
            push_SeqStack(myStack,pStr);
            pStr++;
            continue;
        }
        if(*pStr=='+' || *pStr=='-' || *pStr=='*' || *pStr=='/'){
            if(isEmpty(myStack)){ //若栈为空，直接入栈
                push_SeqStack(myStack,pStr);
                pStr++;
                continue;
            } else{ //栈不为空就需要比较优先级
                if(priority(pStr) > priority(top_SeqStack(myStack))){
                    push_SeqStack(myStack,pStr);
                    pStr++;
                    continue;
                } else{
                    char *tempChar = top_SeqStack(myStack);
                    temp[index++]=*tempChar; //将栈顶元素给数组，并弹出栈
                    pop_SeqStack(myStack); //栈顶元素出栈
                    push_SeqStack(myStack,pStr); //进栈
                    pStr++;
                    continue;
                }
            }
        }

        if(*pStr==')'){
            while (size_SeqStack(myStack)>0){
                char *tempChar = top_SeqStack(myStack); //先获取栈顶元素
                if(*tempChar=='('){
                    pop_SeqStack(myStack);
                    pStr++;
                    break;
                } else{
                    temp[index++]=*tempChar;
                    pop_SeqStack(myStack);
                }
            }
        }

    }

    if(!isEmpty(myStack)){  //栈不为空，依次把剩余的元素加入到字符数组中
        while (size_SeqStack(myStack)>0){
            char *tempChar = top_SeqStack(myStack); //先获取栈顶元素
            temp[index++]=*tempChar;
            pop_SeqStack(myStack);
        }
    }

    //printf("%d", size_SeqStack(myStack)); //说明到这里的时候就是空栈了
    //字符数组剩余的未赋值的空间，是‘\0’
    for (int i = 0; i < strlen(str); ++i) {
        printf("%c  ",temp[i]);
    }

    //此时计算完后缀表达式的栈是空的，可以重复利用
    printf("%.1f",calculate(myStack,temp));
}



int main() {
    test02();
    //printf("Hello, World!\n");
    return 0;
}

二叉树（遍历，树高，叶子数，拷贝二叉树，释放二叉树）（递归法实现）

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

struct BinaryNode{
    char ch; //数据域
    struct BinaryNode *lChild; //左孩子
    struct BinaryNode *rChild; //右孩子
};

//遍历二叉树
void recursion(struct BinaryNode *root){
    if(root==NULL){
        return;
    }

    //前序遍历 根左右
    printf("当前节点的值为:%c\n",root->ch); //打印当前节点的值
    if(root->lChild!=NULL){
        recursion(root->lChild);
    }

    if(root->rChild!=NULL){
        recursion(root->rChild);
    }

    //中序遍历
//    recursion(root->lChild);
//    printf("当前节点的值为:%c\n",root->ch); //打印当前节点的值
//    recursion(root->rChild);
}

//二叉树的计算
void calculateLeafNum(struct BinaryNode *root,int *num){
    if(root==NULL){
       return ;
    }

    if(root->lChild==NULL && root->rChild==NULL){
        (*num)++;
    }
    calculateLeafNum(root->lChild,num);
    calculateLeafNum(root->rChild,num);
}

//树高
int getTreeHeight(struct BinaryNode *root){
    if(root==NULL){
        return 0;
    }

    int lHeight = getTreeHeight(root->lChild);
    int rHeight = getTreeHeight(root->rChild);

    int height = lHeight>rHeight? lHeight+1 : rHeight+1;
    return height;
}

struct BinaryNode *copyBinaryTree(struct BinaryNode * root){
    if(root==NULL){
        return NULL;
    }

    //先拷贝左子树
    struct BinaryNode *lchild = copyBinaryTree(root->lChild);

    //再拷贝右子树
    struct BinaryNode *rchild = copyBinaryTree(root->rChild);
    //创建新的节点
    struct BinaryNode *newNode = malloc(sizeof(struct BinaryNode)); //在堆空间中，开辟一个空间，存储节点

    newNode->ch=root->ch;
    newNode->lChild=lchild;
    newNode->rChild=rchild;

    //返回给用户
    return newNode;
}

void freeBinaryTree(struct BinaryNode *root){
    if(root==NULL){
        return;
    }

    //先释放左子树
    freeBinaryTree(root->lChild);
    //先释放右子树
    freeBinaryTree(root->rChild);
   //释放根节点
    free(root);
}

void test01(){

    struct BinaryNode NodeA={'A',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeB={'B',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeC={'C',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeD={'D',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeE={'E',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeF={'F',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeH={'H',NULL,NULL}; //初始化一个节点
    struct BinaryNode NodeG={'G',NULL,NULL}; //初始化一个节点

    //构建关系
    NodeA.lChild=&NodeB;
    NodeA.rChild=&NodeF;

    NodeB.rChild=&NodeC;

    NodeC.lChild=&NodeD;
    NodeC.rChild=&NodeE;

    NodeF.rChild=&NodeG;

    NodeG.lChild=&NodeH;

    //遍历节点
    //recursion(&NodeA);

    //统计二叉树中的叶子的数量
    int num=0; //局部遍历必须赋初值，只有全局，结构体这些，再堆空间或者常量池的中的，可以不用赋初值
    calculateLeafNum(&NodeA,&num);
    printf("%d\n",num);

    //获得树的高度
    int height=getTreeHeight(&NodeA);
    printf("%d\n",height);

    //拷贝一个二叉树
    printf("------------------------\n");
    struct BinaryNode * newNode = copyBinaryTree(&NodeA);
    recursion(newNode);

    //释放二叉树
    freeBinaryTree(newNode);
}


int main(){

    test01();
    printf("hello,world!");
    return 0;
}

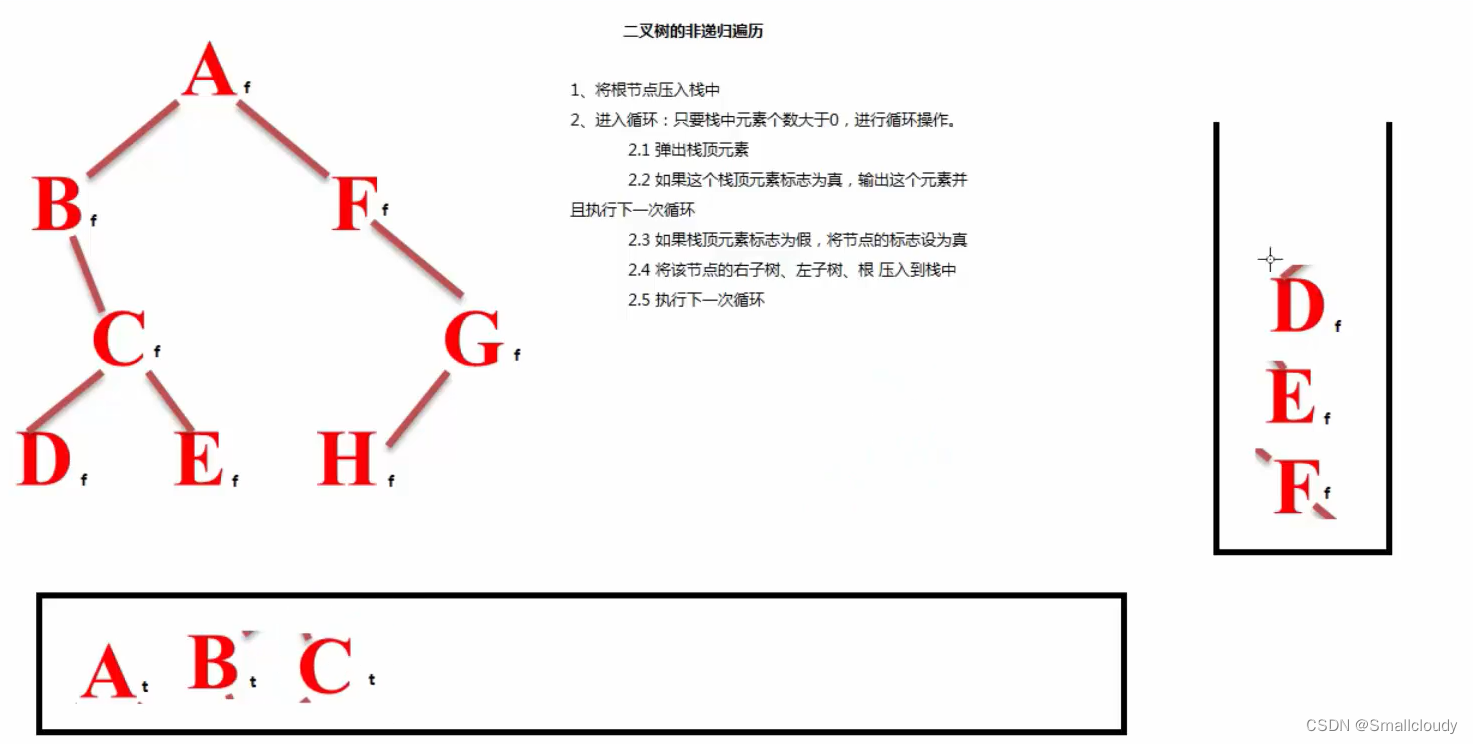
非递归法，利用栈实现对二叉树的遍历

clion中，对多行进行编辑，同时按住alt+shift对多行进行编辑

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "stackFinishByArray.h" //利用数组实现的栈来对二叉树进行遍历

struct BinaryNode{
    char ch; //数据域
    struct BinaryNode *lChild; //左孩子
    struct BinaryNode *rChild; //右孩子
    int flag;
};

void nonRecursionBinaryTree(struct BinaryNode *root){
    if(root==NULL){
        return;
    }

    seqStack myStack = init_Stack(); //先初始化一个空栈
    //将根节点压入栈中
    push_SeqStack(myStack,root);
    //当栈中元素大于0时，执行循环
    while (size_SeqStack(myStack)>0){
        //首先拿出栈顶元素
        struct BinaryNode *topNewNode = top_SeqStack(myStack);
        pop_SeqStack(myStack);
        //栈顶元素为真，直接输出
        if(topNewNode->flag==1){
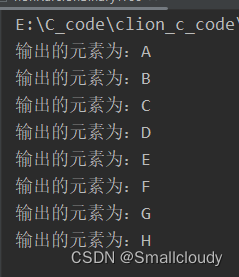
            printf("输出的元素为：%c\n",topNewNode->ch);
            continue;
        }
        //如果栈顶元素为假，则改为真
        topNewNode->flag=1;
        //并将该节点的右子树，左子树，根压入栈中
        if(topNewNode->rChild!=NULL){
            push_SeqStack(myStack,topNewNode->rChild);
        }
        if(topNewNode->lChild!=NULL){
            push_SeqStack(myStack, topNewNode->lChild);
        }
        push_SeqStack(myStack,topNewNode);

    }

    //销毁这个栈
    destroy_SeqStack(myStack);
    myStack=NULL;
}

void test03(){
    struct BinaryNode NodeA={'A',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeB={'B',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeC={'C',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeD={'D',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeE={'E',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeF={'F',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeH={'H',NULL,NULL,0}; //初始化一个节点
    struct BinaryNode NodeG={'G',NULL,NULL,0}; //初始化一个节点

    //构建关系
    NodeA.lChild=&NodeB;
    NodeA.rChild=&NodeF;

    NodeB.rChild=&NodeC;

    NodeC.lChild=&NodeD;
    NodeC.rChild=&NodeE;

    NodeF.rChild=&NodeG;

    NodeG.lChild=&NodeH;

    nonRecursionBinaryTree(&NodeA);

}
int main(){
    test03();
    return 0;
}

更改文件的输出编码格式