矩阵A可以LU分解的充要条件

矩阵A可以LU分解的充要条件是
∀ k ∈ { 1 , ⋯   , n } , r a n k A 1 : k , 1 : k + k ⩾ r a n k A 1 : k , 1 : n + r a n k A 1 : n , 1 : k \forall k \in \{1,\cdots,n\}, \mathrm{rank} A_{1:k,1:k} + k \geqslant \mathrm{rank} A_{1:k,1:n} + \mathrm{rank} A_{1:n,1:k} ∀k∈{1,⋯,n},rankA1:k,1:k​+k⩾rankA1:k,1:n​+rankA1:n,1:k​.

如果矩阵A可以LU分解, 分解的唯一性需要通过下式分析
$Ly=f$, $Ux=y$.

下面给出一个分解算法.

1. INPUT $A\in {\mathcal{M}}_{n\times n}(\mathcal{F})$
2. FOR $k=1,\cdots ,k$ DO
   1. IF $A=0$ THEN
      1. $L_{:,k}\leftarrow 0$
      2. $U_{k,:}\leftarrow 0$
   2. ELSE
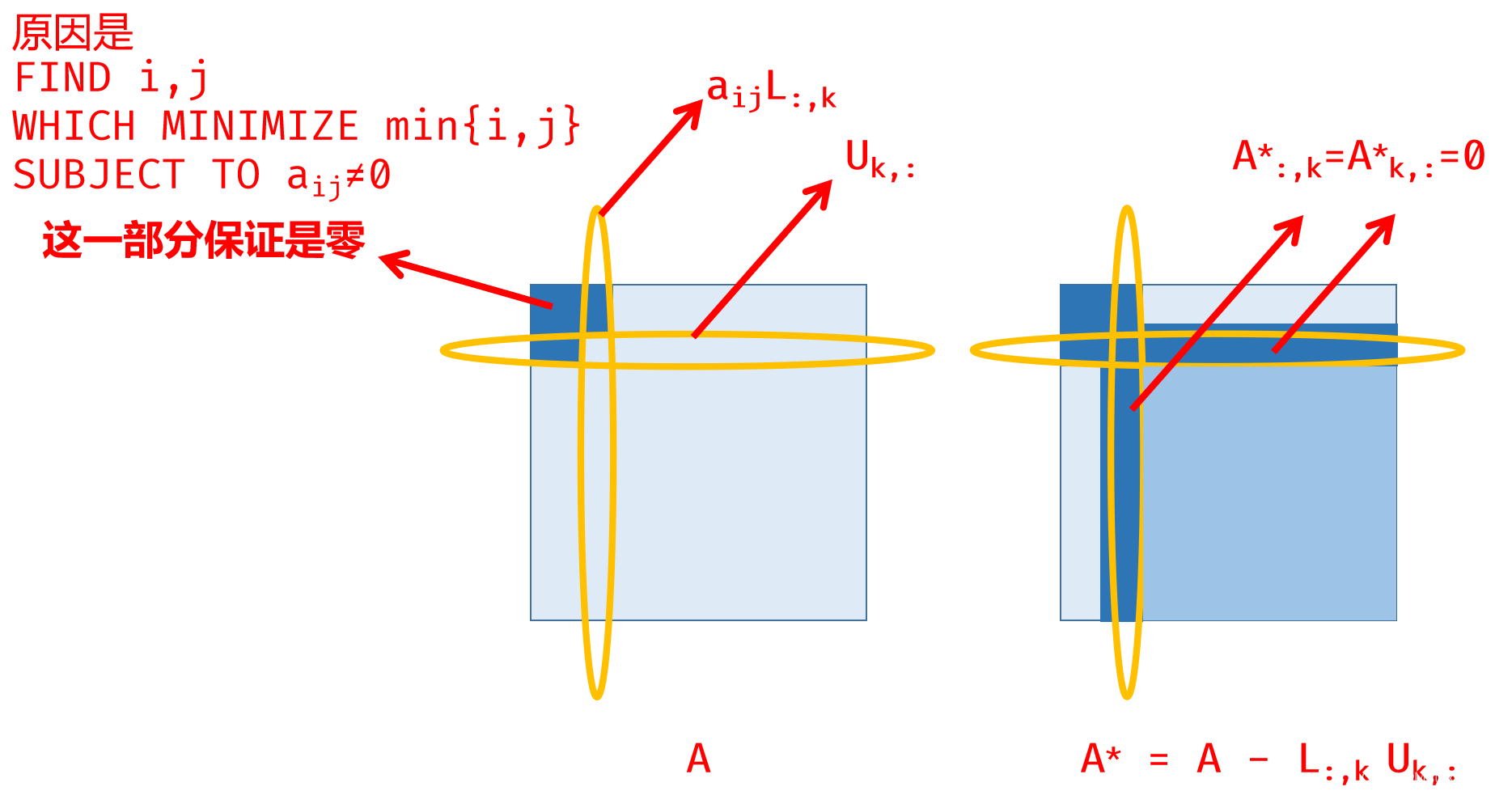
      1. FIND $i,j,$ WHICH MINIMIZE min ⁡ { i , j } \min\{i,j\} min{i,j} SUBJECT TO $a_{ij}\ne 0$
      2. $L_{:,k}\leftarrow a_{ij}^{-1}{A}_{:,j}$
      3. $U_{k,:}\leftarrow A_{i,:}$
      4. $A\leftarrow A-L_{:,k}{U}_{k,:}$
   3. END IF
3. END FOR
4. OUTPUT $L$, $U$,

参考文献
Pavel Okunev, Necessary And Sufficient Conditions For Existence of the LU Factorization of an Arbitrary Matrix.

书上的定理7.3是
矩阵A可以LU分解的充分条件是
$A$的顺序主子式$D_i\ne 0$($i=1,2,\cdots ,n-1$)
此时分解是唯一的.