ES算法

ES(Evolutionary Strategy)

在20世纪60年代初，柏林工业大学的I. Rechenberg和H.-P. Schwefel等在进行风洞实验时，由于在设计中描述物体形状的参数难以用传统的方法进行优化，从而他们利用生物变异的思想来随机地改变参数值并获得了较好的结果。随后，他们便对这种方法进行了深入的研究和发展，形成了演化计算的另一个分支—演化策略。

关键理念：“演化的演化”

以个体的变异算子为主，重组算子为辅

认为变异强度是演化的关键，称为演化策略参数

将演化策略参数纳入演化本身，不断优化参数

演化策略的基本框架

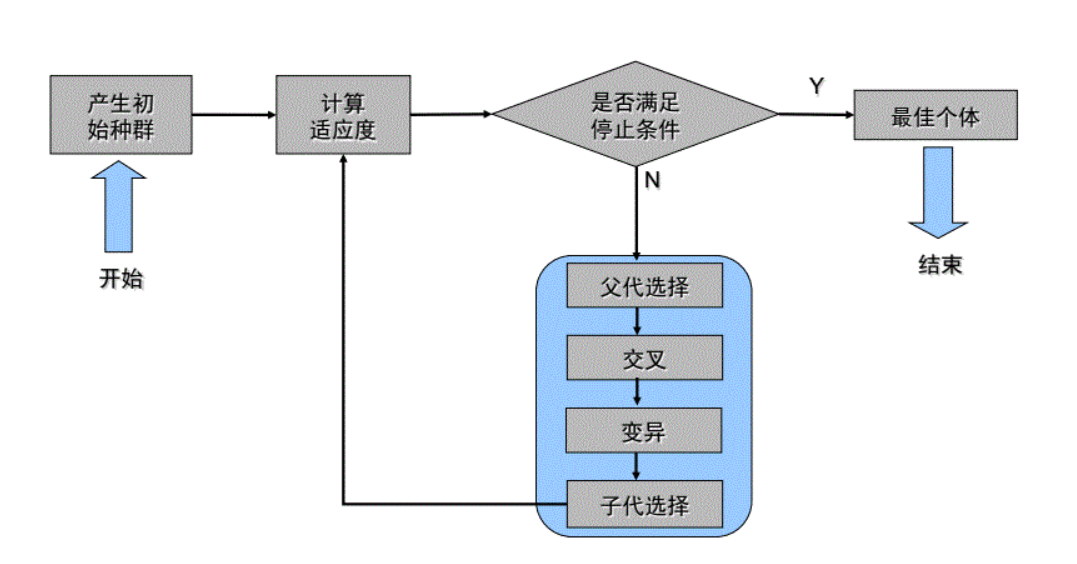
QQ截图20200428193928.png

个体表示：
(x1,x2,…,xn,σ1,σ2,…,σn)，前面的x为一个个体n维，而后面的σ为此个体的各个维度变异强度。一个个体的强度可以相同

接下来介绍ES算法的主要部分——变异和生存选择：

ES算法的变异对于使用这个算法的人来说也是非常友好的，因为它也和EP一样直接给出了公式：

QQ截图20200428194801.png

当μ个父代个体的都产生了子代，那么就会存在μ+μ个个体，如何从这μ+μ个个体中选出下一代呢？这个就是生存选择索要解决的事情，我们可以采用(μ+μ)随机q竞争选择，也可以简单排序择优选择。

当然ES相较于EP还多了一个重组，这里的重组对于变量部分是全局重组，要想重组出一个子代，那就要随机选取2倍维度数量的父代然后从每两个父代中诞生子代的每一维，至于怎么诞生，可以从两个父代的第随机个维随机选择一个。 策略部分的重组则是采用这两个父代的第随机个维的均值。当然重组这个模块对于演化策略似乎并不是太重要。

有了这些东西我们就可以编出相应的代码：

function [answer,best]=ESpro(fun)
global popnum ubound lbound vs dim cost times
best=inf;
answer=zeros(times,cost/popnum);
for i=1:times
    [X,D]=initpop();
    for j=1:(cost/popnum) 
        [newX,newD]=rcb(X,D);
        [newX,newD]=variant(newX,newD);
        [luck,fa]=selecsur(X,newX);
        x=[X;newX];
        X=x(luck,:);
        d=[D;newD];
        D=d(luck);
        last=keepbest(fa);
        answer(i,j)=last;
        if last<best
            best=last;
        end
    end
end

function [X,D]=initpop()
X=unifrnd(lbound,ubound,popnum,dim);
D=unifrnd(0,ubound,popnum,1);
end

function [newX,newD]=rcb(X,D)
newX=zeros(popnum,dim);
for i1=1:popnum
    for j1=1:dim
        select=randperm(popnum,2); %随机选出两个父代个体的下标
        choose=X(select,:); %提取被选中的父代个体
        newX(i1,j1)=choose(unidrnd(2),j1); %重被选中的父代个体中随机选择一个
    end
end
newD=zeros(popnum,1);
for i2=1:popnum
    select=randperm(length(D),2);
    choose=D(select);
    newD(i2)=mean(choose);
end
end

function [newX,newD]=variant(X,D)
newX=zeros(popnum,dim);
newD=zeros(popnum,1);
rho0=randn();
rho=randn(popnum,1);
for i3=1:popnum 
    newD(i3)=D(i3)*exp(sqrt(2*popnum)*rho0+sqrt(2*sqrt(popnum))*rho(i3));
    if newD(i3)<vs
        newD(i3)=vs;
    end
    for j3=1:dim
        newX(i3,j3)=X(i3,j3)+newD(i3)*randn();
    end
end
end

function f=fit(X)
f=zeros(length(X),1);
for i4=1:length(X)
    f(i4)=fun(X(i4,:));
end
end

function [luck,fa]=selecsur(X,newX)
X=[X;newX];
f=fit(X);
[~,b]=sort(f);
luck=b(1:length(b)/2);
fa=f(luck);
end
end
function best=keepbest(X)
best=min(X);
end

测试branin函数:

global popnum ubound lbound vs dim cost times
popnum=50; %种群数量
ubound=15; %个体维度大小上限
lbound=-5; %个体维度大小下限
vs=0.3;  %变异强度临界值
dim=2;   %个体维度大小
cost=20000;  %计算代价
times=30;   %重复计算次数
fun=@(x)(x(2)-(5.1/(4*pi^2))*x(1)^2+5*x(1)/pi-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
[answer,best]=ESpro(fun) %best为ES找到的最优值，answer为每次计算得到的最好结果变化矩阵
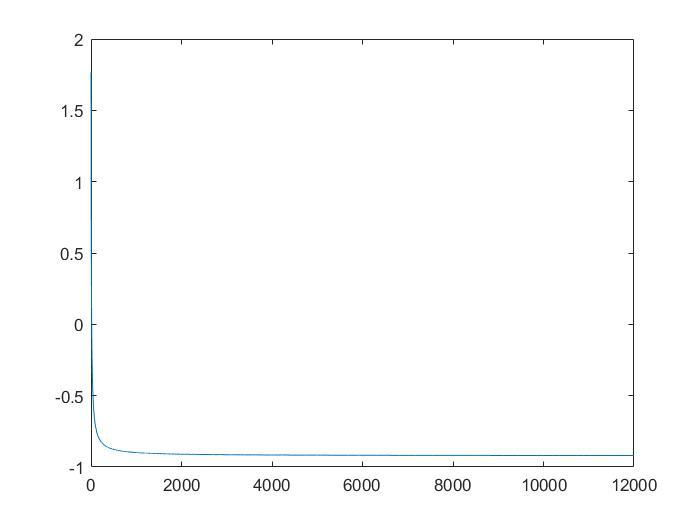
plt(answer);
function plt(answer)  %绘制L曲线图
hisbest=reshape(answer',1,size(answer,1)*size(answer,2));
hisbest(1)=max(hisbest);
for k=2:length(hisbest)
    if hisbest(k)>hisbest(k-1)
        hisbest(k)=hisbest(k-1);
    end
end
for t=2:length(hisbest)
    hisbest(t)=(hisbest(t)+hisbest(t-1)*(t-1))/t;
end
plot(log(hisbest));
hold on
end

结果如下：
es.jpg