格密码基础:子格,q-ary垂直格与线性代数
目录
一.写在前面
格密码中的很多基础原语都来自于线性代数的基本概念,比如举几个例子:
格密码中的非满秩格------------矩阵的秩,矩阵列向量的线性独立性
格基正交化过程------------------正交矩阵的性质与变换
子格---------------------------------矩阵子空间
正交子格---------------------------正交子空间
q-ary垂直格-----------------------向量与矩阵列空间垂直
本文章将解释线性代数中的子空间,正交矩阵,零空间,矩阵的秩在格密码中的运用。
二.子空间垂直
2.1 理论解释
一个点:0维度
一条线:1维度
一个平面:2维度
一个立体图形:3维度
以此类推。。。。。
子空间垂直要求:一个子空间中的任意向量与另一子空间中的任意向量都垂直。
比如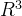 的子空间维度可以是0,1,2,3。0维的子空间只能是原点
的子空间维度可以是0,1,2,3。0维的子空间只能是原点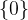 (如果选其他点的话,必然构成一条线),当然按照惯例,原点形成的0维子空间与任意子空间都垂直。
(如果选其他点的话,必然构成一条线),当然按照惯例,原点形成的0维子空间与任意子空间都垂直。
子空间垂直领域,一条线可以跟一条线垂直,一条线可以跟一个平面垂直,但注意一个平面和一个平面不可能垂直。
注意:此处与以前高中学习的平面垂直是不一样的。
举个例子:
一间教室前面的墙和侧边的墙,我们感觉是垂直的。但不符合子空间垂直的概念,你沿着角落那条线,在前面墙画一条竖线,在侧面墙画一条竖线,这两条竖线很明显平行,并不垂直。
总结以上,子空间垂直的官方定义如下:
Two subspaces V and W of the same space 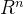 are orthogonal if every vector v in V is orthogonal to every vector w in W:
are orthogonal if every vector v in V is orthogonal to every vector w in W: 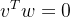 for all v and w.
for all v and w.
2.2 举例分析
给出两个向量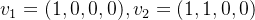 ,很明显这两个向量形成的子空间V为2维的平面。给出向量
,很明显这两个向量形成的子空间V为2维的平面。给出向量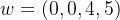 ,很明显这一个向量形成的子空间W为一条线。
,很明显这一个向量形成的子空间W为一条线。
根据向量垂直的基础知识,很容易验证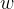 既与
既与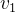 垂直,也与
垂直,也与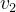 垂直。
垂直。
接着很容易推导出,子空间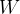 与子空间
与子空间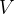 互相垂直。
互相垂直。
在这个例子里面,V的维度是2,W的维度是1,总空间大小是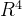 ,说明还缺一个维度。再给出一个向量
,说明还缺一个维度。再给出一个向量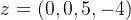 ,该向量形成的子空间为L,很明显它既垂直于V,又垂直于W。现在把它们的维度加在一起:2+1+1=4,刚刚好。
,该向量形成的子空间为L,很明显它既垂直于V,又垂直于W。现在把它们的维度加在一起:2+1+1=4,刚刚好。
三. 零空间
3.1 零空间与q-ary垂直格
对于正整数n和q,选出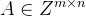 (密码学通常要求该矩阵随机取),这个矩阵是公开的,如果有一个向量z乘以该矩阵为0向量,那么把满足此条件的向量z全部都组合在一起,就称之为q-ary垂直格,如下:
(密码学通常要求该矩阵随机取),这个矩阵是公开的,如果有一个向量z乘以该矩阵为0向量,那么把满足此条件的向量z全部都组合在一起,就称之为q-ary垂直格,如下:
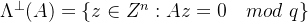
仔细观察此处的向量z,这不就是线性代数中的零空间!后续讨论中,我们用x来代替z,代表其在线性代数中可以取非整数,如下:

矩阵A的行向量都是n维的,所以行空间是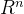 的子空间。向量x也是n维的,所以此零空间也是
的子空间。向量x也是n维的,所以此零空间也是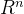 的子空间。
的子空间。
3.2 零空间与行/列空间
定理
- 在
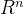 上,行空间与零空间互相垂直;
上,行空间与零空间互相垂直; - 在
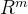 上,列空间与左零空间互相垂直;
上,列空间与左零空间互相垂直;
证明:
给定任意m行n列矩阵A,从其零空间中抽取一个n维向量x,满足Ax=0,该方程组有m个方程,可以理解为矩阵A的每一行都与向量x相乘,如下:
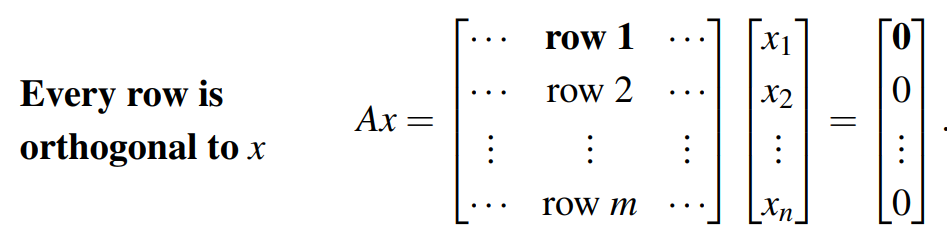
第一行与向量x的内积为0,所以第一行与向量x垂直。以此类推,向量x与每一行都垂直。也就是向量x与每一行的任意线性组合都垂直。这不就是零空间内任意向量x都与行空间内任意向量垂直,写作:
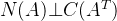
矩阵的列空间也有类似的性质。比如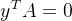 ,如下:
,如下:
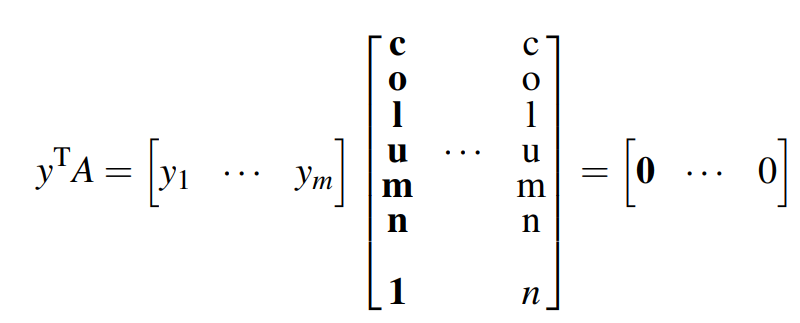
向量y垂直于矩阵A的每一列。向量y形成的空间就是所谓的左零空间。通常写作:
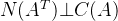
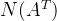 代表左零空间,C(A)代表矩阵A的列空间。
代表左零空间,C(A)代表矩阵A的列空间。
3.3 举例
给定一个秩为1的矩阵A,如下:
![A=\left[ \begin{array}{cc} 1& 3 \\ 2&6\\ 3&9 \end{array} \right]](https://images2.imgbox.com/8a/e5/iXToait9_o.png)
由此可得该矩阵的行空间和列空间均为一条线。观察发现矩阵A的每一行都是向量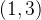 的倍数,由此可类推其零空间中包含向量
的倍数,由此可类推其零空间中包含向量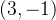 ,该向量与矩阵A的任意行都垂直,如下:
,该向量与矩阵A的任意行都垂直,如下:
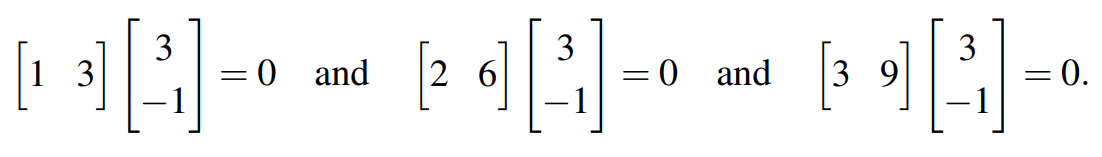
行空间的维度为1,零空间的维度也为1,总维度为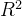 。总结出规律:
。总结出规律:
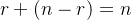
列空间是过点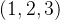 的一条线,左零空间的点记为
的一条线,左零空间的点记为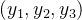 ,根据
,根据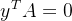 ,需要满足:
,需要满足:
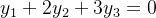
这不就是一个平面。总结规律:
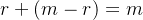
四. 格密码相关
格密码的SIS问题与矩阵正交相关。
结论1:

理解:零空间是行空间的正交补集。
结论2:
行空间维度+零空间维度=矩阵列数
列空间维度+左零空间维度=矩阵行数
结论3:
左零空间在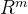 上是列空间的正交补集。
上是列空间的正交补集。