【数字信号处理】FIR 滤波器基础理论
FIR 滤波器设计基础理论
FIR 滤波器是数字滤波器的一种,相比于模拟滤波器,其滤波精度高,稳定,可随时修改,不需要考虑阻抗等问题,可以实现特殊要求的幅频特性,同时满足一定条件的FIR滤波器具有线性相位,因此FIR滤波器在实际工程中得到了较为广泛的应用,例如图像处理、通信以及雷达等。
本文主要讲述线性相位的 FIR 滤波器的基本原理和
并行结构基础,其次阐述了并行结构中常用到的 FFA 算法和快速卷积算法。
1.FIR 滤波器的基本原理
一个 N 阶的 FIR 滤波器输出公式 y(n) 如下:
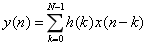
式1中 h(k)为滤波器的系数,x(n-k)为x(n)延时k个周期。系统的传输函数H(z)可表示成公式2:
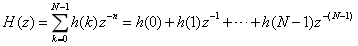
从式1看出:滤波过程主要是一组特定的系数与信号完成卷积的过程。从式2看出,在有限的Z平面内它有N-1个零点同时其 N-1个极点全部位于 z=0 中,因此 FIR 滤波器也被称为全零点滤波器,是一个单位脉冲响应有限长的稳定系统。
FIR滤波器在系数满足一定条件的情况下,它的相频特性是线性的,可以有效的保留信号的相位信息,因此线性相位的 FIR 滤波器在实际工程中有着较为广泛的应用。FIR网格结构的特点是没有反馈支路,也就是说没有环路。下面将介绍三种 FIR滤波器中常用到的网格结构。
1.1 FIR 滤波器基本结构
直接型:按照公式1或者2直接画出的结构就是直接型结构。直接型结构是将公式中的x(n-k)延时链展开,将延时后的数据先进行乘法运算后进行累加操作,如图 1 所示。将直接型结构进行转置(转置原理),先进行乘法运算后续进行延时
和累加操作即可得到转置型网格结构,如图2 所示。
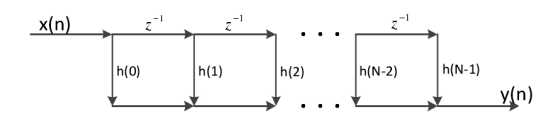
图1 直接型网格结构
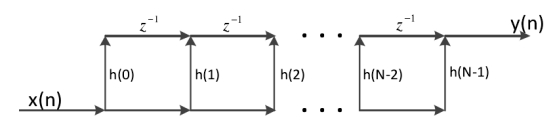
图2 转置型网格结构
级联型:把系统函数进行因式分解,将其中成对的零点排列在一起,得到 1 阶或者2 阶的基本直接型结构,将基本结构互相级联即可得到级联结构。
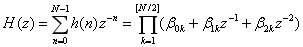
式3中[N/2]表示对 N/2 取整。当 N 为奇数的时候,为 0。FIR 滤波器的级联结构如图 2.3 所示。
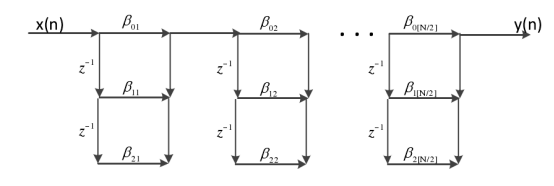
图2.3 级联型网格结构
级联型结构使用的乘法器较多,滤波器阶数越高越难分解,因此在实际中应用较少。
**线性相位结构:**FIR 滤波器因其线性相位特性和系数对称性而在实际工程中被广泛使用,可以保留初始相位信息。它的单位脉冲响应满足如下公式4:
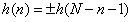
式4中,+表示第一类线性相位结构,-表示第二类线性相位结构。当 N 为偶数时:
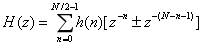
当 N 为奇数时:
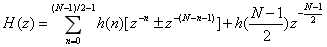
因此,根据公式画出线性相位结构如下:
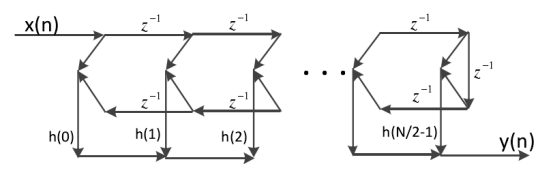
(a)N为偶数
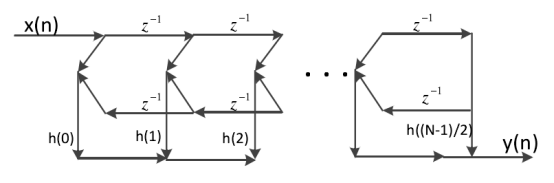
(b)N为奇数
图4 第一类线性相位网格结构
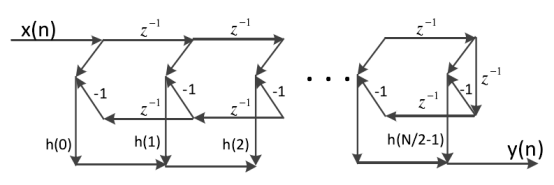
(a)N为偶数
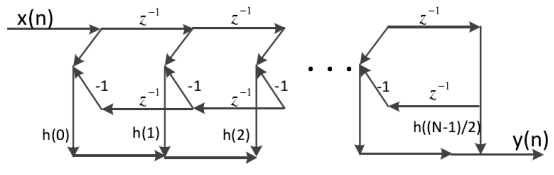
(b)N为奇数
图5 第二类线性相位网格结构
线性相位结构中,通常使用第一类线性相位结构的 FIR 滤波器。按照线性相位结构,FIR 滤波器在实现时可利用系数对称性节省一半乘法器,但同时,输入至乘法器的信号会额外展宽一位。在实际工程中,加法实现简单,但乘法器是重要资源,因此,线性相位结构得以在各个硬件平台中应用。
何时需要用到FIR滤波器
如果在硬件电路处理后任然有噪声,此时就可以考虑采用滤波器,如果所用芯片算力不错,就可以考虑采用FIR滤波器
如果在硬件也能实现有源滤波器能解决产品中的噪声干扰,但是发现硬件的方法需要成本比较高,或者PCB面积受限时,也推荐考虑采用数字滤波器实现。因为往往有源滤波器要实现一个比较好的通频带高Q值时,其阶数往往很高,而且可能需要一些特殊规格的电阻电容实现所需的频带,此时数字滤波器仅需要一段代码搞定,而且效果往往比硬件滤波器更好也更灵活。
如果在系统中发现采用IIR拓扑类型滤波器无法满足线性相位需求,或者发现使用IIR滤波器,滤波器输出出现严重失真或者不稳定现象时,推荐考虑采用FIR滤波器。