【论文阅读笔记】Learning high-speed flight in the wild
链接
论文原址:https://www.science.org/doi/abs/10.1126/scirobotics.abg5810
github:https://github.com/uzh-rpg/agile_autonomy
前言
现有的传统导航方法分为几个子任务:感知、建图、规划,这篇文章的motivation是认为这样的几个任务按顺序执行,第一个问题是模块之间的交互需要时间,降低了效率,第二是这样顺序执行有可能放大了整个pipeline的错误。因此这篇文章尝试单纯利用双目视觉信息(深度图)和位姿,结合神经网络,生成控制信息,实现了无人机真实场景的高速飞行。
方法
专家支路
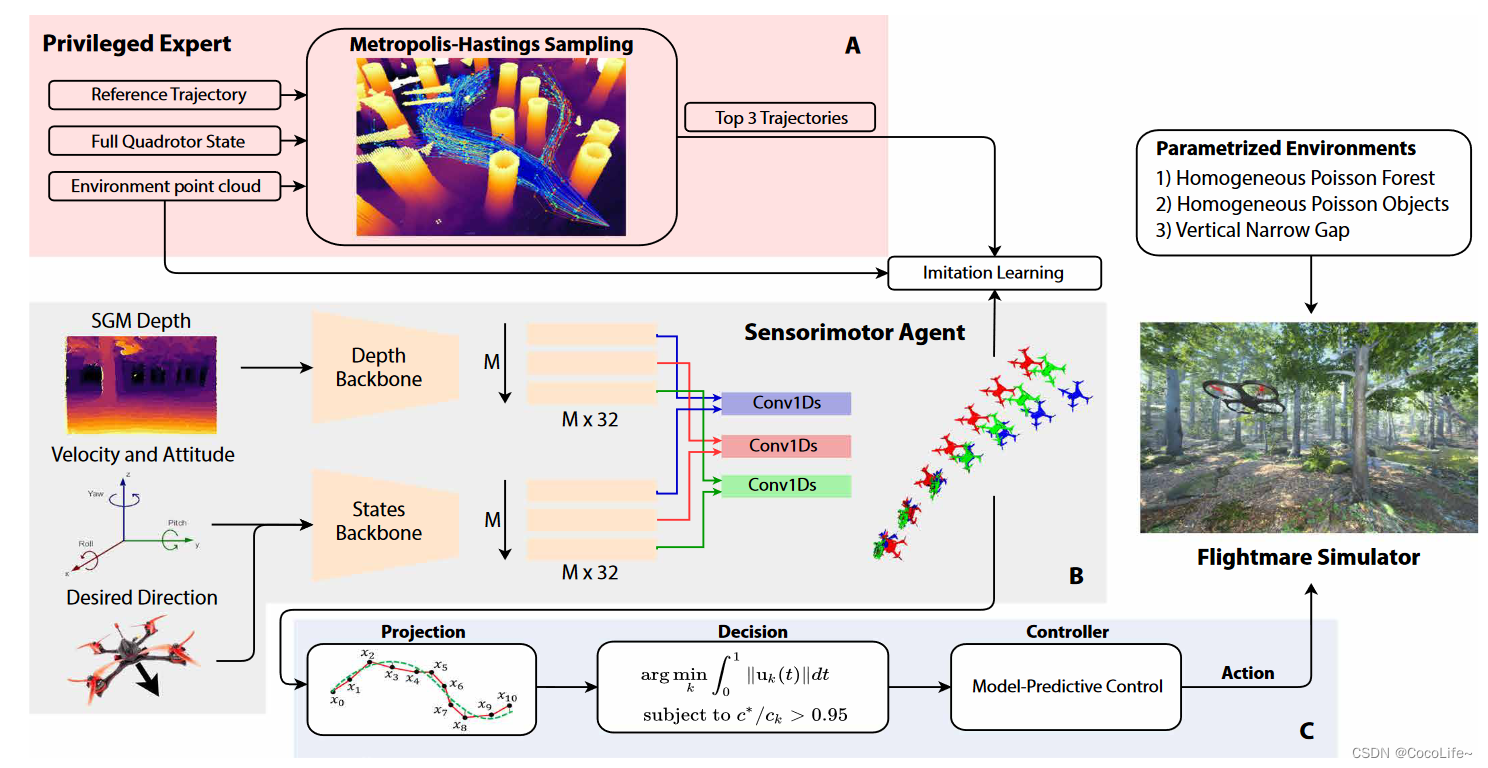
先看方法,整个论文的框架图如上所示,看起来还是比较直观,首先是在仿真中,有着更充分先验知识的专家(A部分区域),专家支路在进行路径规划时,对整个平台和地图的状态有充分了解,在此基础上生成一组collision free的路径,这个路径或轨迹是满足以下概率分布的:
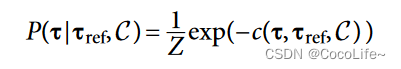
其中Z是一个归一化系数,是对P在整个轨迹
τ
τ
τ求积分的结果。
c
(
τ
,
τ
r
e
f
,
C
)
c(τ,τ_{ref},C)
c(τ,τref,C)是一个计算cost的函数,遵从如下公式:
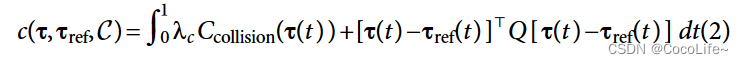
其中积分中的前半项,
λ
c
λ_c
λc=1000,
C
c
o
l
l
i
s
i
o
n
C_{collision}
Ccollision是碰撞代价,这里
r
q
r_q
rq设置的是0.2,说白了就是距离点云地图
C
C
C中的障碍物越远,碰撞代价越低,达到2倍仿真无人机半径时取0。
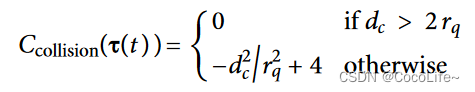
积分后半项,
Q
Q
Q是一个状态成本矩阵(半正定),这里文章好像没写是怎么设定的,后续复现的时候再看看代码里吧~,但总的来说后半项计算的是生成的轨迹与参考轨迹的差值与状态成本的联系,是希望尽量靠近参考轨迹。
总的来说,这个路径的概率分布即越靠近参考路径、越远离
C
C
C中障碍物,cost越小,P越大。
这个P其实是难以计算的,因为障碍物的多样性、混乱的环境等原因。本文的专家支路采用M-H算法进行采样,去逼近最真实的分布。MH算法的·目标分数函数定义为 s ( τ ) = exp ( − c ( τ , τ r e f , C ) ) s(\tau)=\exp \left(-c\left(\tau, \tau_{\mathrm{ref}}, \mathcal{C}\right)\right) s(τ)=exp(−c(τ,τref,C)),其实就是为了生成的样本能够渐进地服从P这个分布。
为了进一步降低采样空间的维数,本文用三次b-样条曲线来逼近路径点,曲线具有三个控制点和一个均匀的节点向量,而且用三次b样条曲线有个什么好处呢,因为是三次b样条具有两次连续可导性,并在闭区间上具有有界的导数。路径的导数、二阶导也就是无人机的速度、加速度,这样的性质也就保证了无人机飞行的连续性。
需要注意的是,专家支路也无法实现高速飞行,因为专家在生成proposal distribution的时候采样生成了大量的轨迹,有较高的计算代价。为了让生成的轨迹更偏向于无碰撞,将 τ r e f τ_{ref} τref替换为计算的全局无碰撞轨迹 τ g b l τ_{gbl} τgbl,这样可以让专家生成更多可以合理的、可以被保留的轨迹,以便最后取最优的三条轨迹供后续学生支路的学习。
agent支路
其次,在B阶段,agent智能体能获取到的信息包括智能体的关注信息o包含:深度图像 640×480
;速度估计
R
3
\mathbb{R}^3
R3;q 旋转矩阵形式表达的姿态
R
3
×
3
\mathbb{R}^{3×3}
R3×3;w 初始飞行方向
R
3
\mathbb{R}^3
R3,仅仅有这样的信息去做导航主要有两个难点:
- 整个环境只能通过有噪声的传感器(深度相机)观察得来。
- 分布P是一个多模态的。而且可能存在多个运动假设都有很高可能性,导致平均的可能性很低的情况。
因此,本位提出通过神经网络对深度和位姿信息进行降维处理,得到控制信息。
τ
n
k
=
[
p
(
t
i
)
]
i
=
1
10
,
t
i
=
i
10
\boldsymbol{\tau}_n^k=\left[\mathbf{p}\left(t_i\right)\right]_{i=1}^{10}, t_i=\frac{i}{10}
τnk=[p(ti)]i=110,ti=10i
这里控制信息是每一秒切分成10份,有十个位置点,这样做一是更general,二是test的时候插值所需的损耗相较于3个控制点的B样条要更低。
损失函数有关生成的轨迹与专家轨迹差的部分:使用relaxed winner-takes-all
R
−
W
T
A
(
T
e
,
T
n
)
=
∑
i
=
0
∣
T
e
∣
∑
k
=
0
∣
T
n
∣
α
(
τ
e
,
p
i
,
τ
n
k
)
∥
τ
e
,
p
i
−
τ
n
k
∥
2
\operatorname{R}-\mathrm{WTA}\left(\mathcal{T}_e, \mathcal{T}_n\right)=\sum_{i=0}^{\left|\mathcal{T}_e\right|} \sum_{k=0}^{\left|\mathcal{T}_n\right|} \alpha\left(\tau_{e, p}^i, \tau_n^k\right)\left\|\tau_{e, p}^i-\tau_n^k\right\|^2
R−WTA(Te,Tn)=∑i=0∣Te∣∑k=0∣Tn∣α(τe,pi,τnk)
τe,pi−τnk
2
但是上式如果只匹配最接近的expert轨迹的话是硬分配,并不可微。为了能进行学习,引入一个小的系数进行软分配,软分配是指为每个网络轨迹分配一个权重值,而不是简单地将其与最接近的专家轨迹匹配。
α
(
τ
e
,
p
i
,
τ
n
k
)
=
{
1
−
ϵ
if
∥
τ
e
,
p
i
−
τ
n
k
∥
2
≤
∥
τ
e
,
p
j
−
τ
n
k
∥
2
∀
j
≠
i
ϵ
M
−
1
otherwise
\alpha\left(\tau_{e, p}^i, \tau_n^k\right)=\left\{\begin{array}{ll}1-\epsilon & \text { if }\left\|\tau_{e, p}^i-\tau_n^k\right\|^2 \leq\left\|\tau_{e, p}^j-\tau_n^k\right\|^2 \forall j \neq i \\ \frac{\epsilon}{M-1} & \text { otherwise }\end{array}\right.
α(τe,pi,τnk)={1−ϵM−1ϵ if
τe,pi−τnk
2≤
τe,pj−τnk
2∀j=i otherwise
这里
1
−
ϵ
1-\epsilon
1−ϵ是0.95,
ϵ
M
−
1
\frac{\epsilon}{M-1}
M−1ϵ设置为0.025,也就是说对于每一条network生成的轨迹,计算离expert产生的三条较佳的轨迹的距离,取最近的赋予高权重,将不同的距离加权相加来近似硬分配,这样就可以近似地优化得到最接近expert轨迹的解。
结合碰撞损失,最后的损失函数为:
L
L
(
T
e
,
T
n
)
=
λ
1
R
−
W
T
A
(
T
e
,
T
n
)
+
λ
2
∑
k
=
0
∣
T
n
∣
(
c
k
−
C
collision
(
τ
n
k
)
)
2
\mathcal{L}_{\mathcal{L}}\left(\mathcal{T}_e, \mathcal{T}_n\right)=\lambda_1 \mathrm{R}-\mathrm{WTA}\left(\mathcal{T}_e, \mathcal{T}_n\right)+\lambda_2 \sum_{k=0}^{\left|\mathcal{T}_n\right|}\left(c_k-C_{\text {collision }}\left(\tau_n^k\right)\right)^2
LL(Te,Tn)=λ1R−WTA(Te,Tn)+λ2∑k=0∣Tn∣(ck−Ccollision (τnk))2
根据经验,为了让前后两项处于同一个量级,手动设置 λ 1 = 10 \lambda_1=10 λ1=10 、 λ 2 = 0.1 \lambda_2=0.1 λ2=0.1
在测试阶段,为了得到整条轨迹,设计用5阶的以t为变量多项式逼近轨迹,以x坐标轴为例,转化为如下的优化问题:
minimize
a
x
∑
i
=
1
10
(
τ
n
,
x
k
,
i
−
a
x
⊤
⋅
T
(
i
10
)
)
2
subject to
s
x
(
0
)
−
a
x
⊤
⋅
T
(
0
)
=
0
s
˙
x
(
0
)
−
a
x
⊤
⋅
T
(
0
)
=
0
s
¨
x
(
0
)
−
a
x
⊤
⋅
T
¨
(
0
)
=
0
\begin{array}{c}\underset{\boldsymbol{a}_x}{\operatorname{minimize}} \sum_{i=1}^{10}\left(\tau_{n, x}^{k, i}-\boldsymbol{a}_x^{\top} \cdot \mathbf{T}\left(\frac{i}{10}\right)\right)^2 \\ \text { subject to } s_x(0)-\boldsymbol{a}_x^{\top} \cdot \mathbf{T}(0)=0 \\ \dot{s}_x(0)-\boldsymbol{a}_x^{\top} \cdot \mathbf{T}(0)=0 \\ \ddot{s}_x(0)-\boldsymbol{a}_x^{\top} \cdot \ddot{\mathbf{T}}(0)=0\end{array}
axminimize∑i=110(τn,xk,i−ax⊤⋅T(10i))2 subject to sx(0)−ax⊤⋅T(0)=0s˙x(0)−ax⊤⋅T(0)=0s¨x(0)−ax⊤⋅T¨(0)=0
把所有的轨迹投影完成后,选一个输入cost最小的(minimum snap)进控制器。
结果
实机飞行,这部分说白了就是在仿真中训练到足够好的参数,再去实际场景(仿真中没有的)进行实机的飞行试验,也就是论文里的zero-shot,但因为学习的时候,仿真和真实世界的输入差不多,这样到没专门训练过的真实场景上之后也不不会有过多的差异,所以实机飞行的结果还是比较好的,这里感兴趣的可以去官网看他们公布的补充材料中的视频。
相关知识补漏
写在最后
- 首先,本文仅为个人的笔记!
- 本人是刚开始学这方面的小白,对论文的学习与掌握难免会出现遗漏,中间的理解如果有错误欢迎大家指正!
- 希望读者可以对我写的内容保持批判精神,欢迎讨论,希望与大家一起进步!
- 另外,其实论文中很多公式理解还是不够深入,后续会对该论文提供的代码进行复现加强自己的理解,咱们下篇文章再见!