纯粹数学作业——Chapter 0

1、列举一个真命题、一个假命题、一个不知道真假的命题、一个不是命题的陈述。

真命题：太阳是发光发热的。

                同位角相等，两直线平行。

假命题：三角形的三个内角和不是180°

不知真假的命题：树叶是黄色的。

不是命题的陈述：可爱的斑马。

2、写出21127的2进制，3进制，8进制，16进制以及36进制的表达形式。

21127 = （101 0010 1000 0111）2 

            = （1001222111）3

           = （51207）8

          = （5287）16

          = （GAV）36

3、证明：1可以除任何整数，任何数可以除0。

（注意，除 和 除以 ，是两个概念）

4、证明： 令a,b,d ∈ Z，假设，d除a, 商为u, d 除b，商为v。u,v为整数。

试证明，d可以除 au+bv。

5、证明： 如果一个整数a, 被b除，余数是r。那么，试证明，如果a 除以（-b），那么余数也为r

6、求408735787基于17进制的展开，以及1442151747基于36进制的展开

（上面两题没有检查！！万一被检查错了，就太丢人了。万一做错了，麻烦给我留言。）

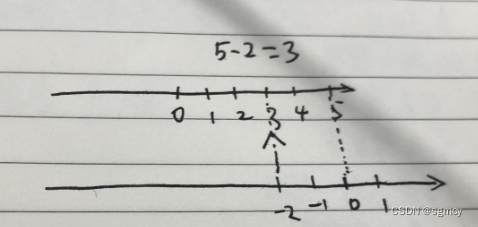
7、将减法和除法运算解释为数轴的几何变换。

加法例子：

乘法例子：

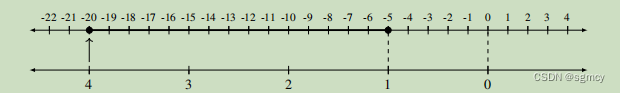
减法例子：

除法例子：

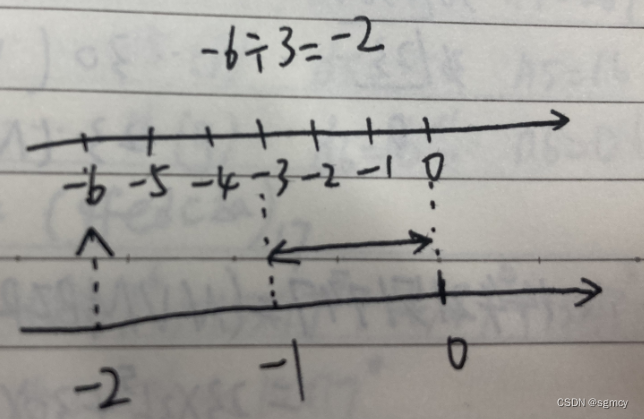
8、证明：令r是一个有理数，a是一个无理数。

证明1：ra是有可能是有理数。

证明2：ra有可能是无理数。

证明1：首先，基于这样一个事实：√ 2是一个无理数。（当然也可以取π）

                令r = 0； a= √ 2 

                ra = 0，是一个有理数（得证）。

 证明2：令r = 1； a= √ 2 

               ra = √ 2 （是一个无理数，得证）

9、写一个4次多项式，基于数集R，而不是数集Q

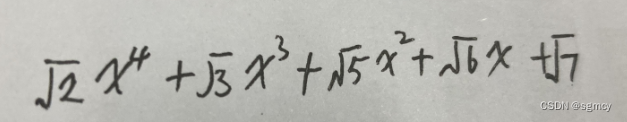
 10、令α = a + bi 是一个复数，a,b ∈ R。试证明，α是一个二项式的根（在R范围内），并且找出另一个根。

11、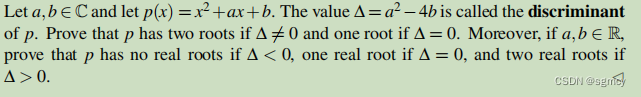

证明：

12、求：

该题与第2题，第6题类似，就不再重复计算。该数值比较大。计算速度比较慢。需要花费时间。

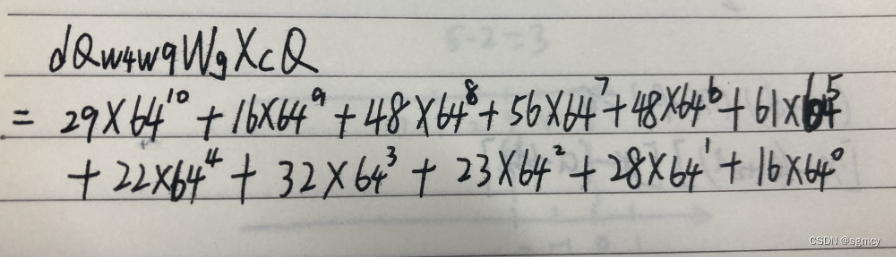
13、

14、

 

15、