大整数的运算
两个大整数(如位数超过1000)的四则运算,显然基本数据类型已经不能保存,因此不能按照一般方法来计算,我们需要声明一个数组来保存每个整数,并且记录长度,即位数。数组中的每一个元素便对应整数当中的每一位,并且数组要提前初始化为0。在存每个数的时候按高位对应数组的高地址,低位对应低地址,即逆向存储。然后按运算法则对数组中的每一个元素即每一位进行运算。
注:为了方便起见,在读入大整数时将其以字符串的形式读入,然后再将其转换为int型存入数组。
一、大整数定义
const int MAX = 1000;//最大长度
typedef struct BigNumber {//大整数
int number[MAX];//保存每一位
int len;//位数
BigNumber() {//构造函数,初始化结构体变量
memset(number, 0, sizeof(number));//初始化数组每一位为0
len = 0;//初始化长度为0
}
};
二、字符串转化为整数
BigNumber convert(string str) { //将字符串转换为整形并保存在数组中
BigNumber a;
int length = str.length();
a.len = length;//保存长度
for (int i = 0; i < length; ++i) {//逐位转换
a.number[i] = str[length - i - 1] - '0';
}
return a;
}
三、两个大整数的比较
#include <iostream>
#include <cstring>
using namespace std;
const int MAX = 1000;
typedef struct BigNumber {
int number[MAX];
int len;
BigNumber() {
memset(number, 0, sizeof(number));
len = 0;
}
};
BigNumber convert(string str) { //将字符串转换为整形并保存在数组中
BigNumber a;
int length = str.length();
a.len = length;//保存长度
for (int i = 0; i < length; ++i) {//逐位转换
a.number[i] = str[length - i - 1] - '0';
}
return a;
}
int compare(BigNumber a, BigNumber b) { //比较a和b的大小
if (a.len > b.len) return 1;//如果a位数多余于b,显然a大
else if (a.len < b.len) return -1;//如果a位数少余于b,显然b大
else {
for (int i = a.len - 1; i >= 0; --i) {//否则从高位到低位逐位比较
if (a.number[i] > b.number[i]) return 1;
if (a.number[i] < b.number[i]) return -1;
}
return 0;
}
}
int main() {
//将两个数视作字符串读入
string s1 = "11456484654874515000";
string s2 = "14687456478415484879";
BigNumber a = convert(s1);
BigNumber b = convert(s2);
cout << compare(a, b) << endl;//1表示a大,-1表示b大,0表示相等
return 0;
}

四、四则运算
1、加法运算
从数组的低位到高位,依次将每一位进行相加,如果有进位,则将进位加到高位。显然,两个个位数相加,最大为十位数,因此将结果中的个位作为和的本位,十位作为进位。
BigNumber Addition(BigNumber a, BigNumber b) { //加法运算
int len1 = a.len;//记录a的长度
int len2 = b.len;//记录b的长度
int carry = 0;//保存进位
BigNumber sum;//和
for (int i = 0; i < len1 || i < len2; ++i) {
int temp = a.number[i] + b.number[i] + carry;//当前位相加再加上进位
sum.number[sum.len++] = temp % 10;//产生进位,则保存个位,向高位进一
carry = temp / 10;//十位上的数作为进位
}
if (carry)//处理最高位上的进位
sum.number[sum.len++] = carry;
return sum;
}
2、减法运算
从低位到高位,逐位用被减数减去减数,如果当前位够减,则保存结果到差中。如果不够减,则被减数向高位借一,低位加十,再进行减法。同时被减数的高位减一。最后处理差中多余的0。
BigNumber Subtraction(BigNumber a, BigNumber b) {//a-b
BigNumber sub;//保存差
for (int i = 0; i < a.len || i < b.len; ++i) {
if (a.number[i] < b.number[i]) {
a.number[i + 1]--;//不够减向高位借一
a.number[i] += 10;//低位加10
}
sub.number[sub.len++] = a.number[i] - b.number[i];//做减法
}
while (sub.number[sub.len - 1] == 0 && sub.len - 1 >= 1) sub.len--;//去掉高位多余的0
return sub;
}
3、乘法运算
对于乘法运算,我们研究高精度与低精度的乘法,即大整数与用基本数据类型可保存的数相乘(这里默认为int型),记大整数为a,int型整数为b,对a从低位到高位,逐位去和b做乘法,得到的积再加上上一步产生的进位,然后将结果的个位保存到最终结果的对应位当中,而高位部分则作为进位。
BigNumber Multiply(BigNumber a, int b) { //乘法运算,注意另一个乘数为int型
int carry = 0;//进位
BigNumber mul;//乘积
for (int i = 0; i < a.len; ++i) {
int temp = a.number[i] * b + carry;//逐位与b相乘并加上进位
mul.number[mul.len++] = temp % 10;//保存个位,高位上的数作为新的进位
carry = temp / 10;//计算进位
}
while (carry != 0) {//处理最高位相乘产生的进位,可能不止一位
mul.number[mul.len++] = carry % 10;
carry /= 10;
}
return mul;
}
4、除法运算
与乘法类似,我们研究高精度与低精度的除法,即大整数与用基本数据类型可保存的数相除(这里默认为int型),记大整数为a,int型整数为b,对a从高位到低位,逐位去和b做除法,上一步产生的余数乘10再加上该位的值,作为当前的被除数,将其和b进行除法运算,如果够除,则当前商对应最终的该位的商,余数作为该步对应的余数;如果不够除,则该位商0。最后注意去掉商中多余的0。
BigNumber Division(BigNumber a, int b, int &r) { // a/b,注意除数为int型,r记录余数
BigNumber div;//商
div.len = a.len;//商的每一位与被除数的每一位一一对应,先令其相等
for (int i = a.len - 1; i >= 0; --i) {
int temp = a.number[i] + r * 10;//临时被除数,为当前位的值加上上一步产生的余数乘10
if (temp >= b) {//够除
div.number[i] = temp / b;//保存商
r = temp % b;//保存余数
} else {//不够除
r = temp;//余数为当前被除数
div.number[i] = 0;//商0
}
}
while (div.number[div.len - 1] == 0 && div.len - 1 >= 1) div.len--;//处理商中多余的0
return div;
}
5、完整代码
#include <iostream>
#include <cstring>
using namespace std;
const int MAX = 1000;
typedef struct BigNumber {
int number[MAX];
int len;
BigNumber() {
memset(number, 0, sizeof(number));
len = 0;
}
};
BigNumber convert(string str) { //将字符串转换为整形并保存在数组中
BigNumber a;
int length = str.length();
a.len = length;
for (int i = 0; i < length; ++i) {
a.number[i] = str[length - i - 1] - '0';
}
return a;
}
int compare(BigNumber a, BigNumber b) { //比较a和b的大小
if (a.len > b.len) return 1;
else if (a.len < b.len) return -1;
else {
for (int i = a.len - 1; i >= 0; --i) {
if (a.number[i] > b.number[i]) return 1;
if (a.number[i] < b.number[i]) return -1;
}
return 0;
}
}
BigNumber Addition(BigNumber a, BigNumber b) { //加法运算
int len1 = a.len;//记录a的长度
int len2 = b.len;//记录b的长度
int carry = 0;//保存进位
BigNumber sum;//和
for (int i = 0; i < len1 || i < len2; ++i) {
int temp = a.number[i] + b.number[i] + carry;//当前位相加再加上进位
sum.number[sum.len++] = temp % 10;//产生进位,则保存个位,向高位进一
carry = temp / 10;//十位数作为进位
}
if (carry)//处理最高位上的进位
sum.number[sum.len++] = carry;
return sum;
}
BigNumber Subtraction(BigNumber a, BigNumber b) {//减法
BigNumber sub;//保存差
for (int i = 0; i < a.len || i < b.len; ++i) {
if (a.number[i] < b.number[i]) {
a.number[i + 1]--;//不够减向高位借一
a.number[i] += 10;//低位加10
}
sub.number[sub.len++] = a.number[i] - b.number[i];//做减法
}
while (sub.number[sub.len - 1] == 0 && sub.len - 1 >= 1) sub.len--;//去掉高位多余的0
return sub;
}
BigNumber Multiply(BigNumber a, int b) { //乘法运算,注意另一个乘数为int型
int carry = 0;//进位
BigNumber mul;//乘积
for (int i = 0; i < a.len; ++i) {
int temp = a.number[i] * b + carry;//逐位与b相乘并加上进位
mul.number[mul.len++] = temp % 10;//保存个位,高位上的数作为新的进位
carry = temp / 10;//计算进位
}
while (carry != 0) {//处理最高位相乘产生的进位,可能不止一位
mul.number[mul.len++] = carry % 10;
carry /= 10;
}
return mul;
}
BigNumber Division(BigNumber a, int b, int &r) { //除法,注意除数为int型,r记录余数
BigNumber div;//商
div.len = a.len;//商的每一位与被除数的每一位一一对应,先令其相等
for (int i = a.len - 1; i >= 0; --i) {
int temp = a.number[i] + r * 10;//临时被除数,为当前位的值加上上一步产生的余数乘10
if (temp >= b) {//够除
div.number[i] = temp / b;//保存商
r = temp % b;//保存余数
} else {//不够除
r = temp;//余数为当前被除数
div.number[i] = 0;//商0
}
}
while (div.number[div.len - 1] == 0 && div.len - 1 >= 1) div.len--;//处理商中多余的0
return div;
}
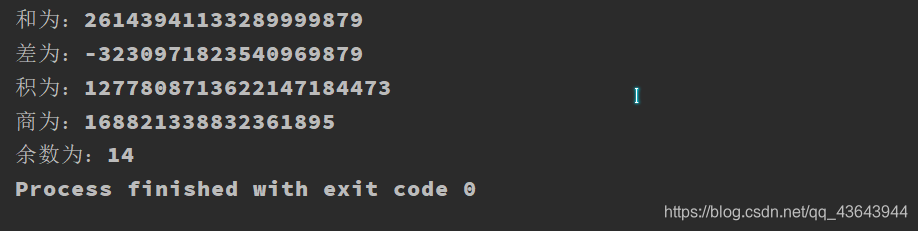
int main() {
//将两个数视作字符串读入
string s1 = "11456484654874515000"; //a
string s2 = "14687456478415484879";//b
BigNumber a = convert(s1);
BigNumber b = convert(s2);
int c = 87, r = 0;//c为除数,r保存余数
BigNumber sum = Addition(a, b);
cout << "和为:";
for (int i = sum.len - 1; i >= 0; --i) {
cout << sum.number[i];
}
cout << endl;
cout << "差为:";
if (compare(a, b) == -1) {
BigNumber temp = a;
a = b;
b = temp;
cout << "-";
}
BigNumber sub = Subtraction(a, b);
for (int i = sub.len - 1; i >= 0; --i) {
cout << sub.number[i];
}
cout << endl;
cout << "积为:";
BigNumber mul = Multiply(a, c);
for (int i = mul.len - 1; i >= 0; --i) {
cout << mul.number[i];
}
BigNumber div = Division(a, c, r);
cout << endl << "商为:";
for (int i = div.len - 1; i >= 0; --i) {
cout << div.number[i];
}
cout << endl << "余数为:" << r;
return 0;
}