八数码(双向BFS和A *和康托展开)
八数码(双向BFS和A * 和康托展开)
https://www.luogu.com.cn/problem/P1379(传送门)
一道题用三种方法来写
题目大意
在3×3的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字。棋盘中留有一个空格,空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
输入格式
输入初始状态,一行九个数字,空格用0表示
输出格式
只有一行,该行只有一个数字,表示从初始状态到目标状态需要的最少移动次数(测试数据中无特殊无法到达目标状态数据)
输入 #1复制
283104765
输出 #1复制
4
样例可变成这样
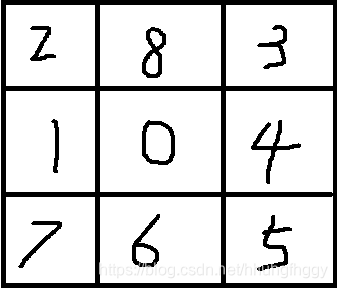
一、康托展开
康托展开
函数cantor()实现的功能是 : 输入一个排列,计算出它的cantor值 即在全排列中是第几个。
例如 12345 cantor值是 1; 12354 cantor值是 2;12435cantor值是 3;
那么如何实现呢?很简单
比如说求2143是{1.2.3.4}的全排列第几大的数
1、比首位2小的只有1这一个数,后面3个数的排列有3!种,所以ans+=1 × \times × 3!;
2、首位为2,比第二位1小的数的个数为0,后面两个数的排列有2!种,所以ans+=0 × \times × 2!;
3、前面为21,比第三位4小的只有3一个(因为前面21已经用了),后面的一个数的排列有1!种,所以ans+=1 × \times × 1!;
4、前三位为214,emmm,不用看也是0了(因为总共只有四位)
总的来说就是
从第一位依次往后遍历,看在未出现的元素中比当前位小的有多少个,然后乘上后面的位数个数的阶乘。累积起来即可。
代码
int cantor(string x){
int len=x.length();
int ans=0;
for(int i=0;i<len;i++){
int t=0;//记录在当前位之后比当前位小的数的个数
for(int j=i+1;j<len;j++){
if(x[j]<x[i])
t++;
}
ans+=t*(len-i-1)!;//阶乘得自己写函数
}
return ans;
}
逆康拓展开
顾名思义就是康托展开的逆过程,在一个集合的全排列中,给你一个数k,求出第k大的排列,即为逆康托展开
代码(限于篇幅,会在代码中注明原理)
void decantor(int k,int n)//n是排列的长度
{
vector<int>p;//存放当前可用的数
vector<int>q;//存放所求排列,用vector主要是觉得比较方便
for(int i=1;i<=n;i++)
p.push_back(i)//将全部能用的数存储进去
for(int i=n;i>=1;i++){
int a=k%(i-1)!;//即减去第一位的个数后剩余的个数
int b=k/(i-1)!;//第一位是由后面的个数的阶乘来乘没出现的元素里比它小的个数,除以阶乘,既可以求出在它后面比它小的有多少个了
k=a;
sort(p.begin(),p.end());
q.push_back(p[b])//因为p是从零开始,所以不需要加一
p.erase(p.begin()+b);//删去使用过的数
}
}
言归正传,接下来用康托展开去重(也可以用map),外加bfs做这道题
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int dx[]={1,0,0,-1};
int dy[]={0,1,-1,0};
int st[9];
int goal[]={1,2,3,8,0,4,7,6,5};
int fuc[]={1,1,2,6,24,120,720,5040,40320,362880};
int mp[1000000];
struct node{
int sum[9];
ll step;
};
bool cantor(int a[]){
ll ans=0;
for(int i=0;i<9;i++){
int z=0;
for(int j=i+1;j<9;j++)
if(a[j]<a[i])
z++;
ans+=fuc[8-i]*z;
}
if(!mp[ans]){
mp[ans]=1;
return 1;
}
else
return 0;
}
queue<node>p;
ll bfs(){
node t;
memcpy(t.sum,st,sizeof(t.sum));
t.step=0;
cantor(st);
if(memcmp(t.sum,goal,sizeof(goal))==0)//特判起点即为终点时
return t.step;
p.push(t);
while(!p.empty()){
t=p.front();
p.pop();
int base;
for(base=0;base<9;base++){
if(t.sum[base]==0)
break;
}//将一维转化为二维
int x=base%3;//横坐标
int y=base/3;//纵坐标
for(int i=0;i<4;i++){
int nx=x+dx[i];//元素0转移后的新坐标
int ny=y+dy[i];
if(nx<0||nx>2||ny<0||ny>2)
continue;
node h;
memcpy(&h,&t,sizeof(struct node));//将t复制给h;
swap(h.sum[y*3+x],h.sum[ny*3+nx]);//这样改变的是h里的值,t的值并未改变。 至于y*3+x是将二维转化为一维
h.step++;
if(memcmp(h.sum,goal,sizeof(goal))==0)
return h.step;
if(cantor(h.sum))//只有之前没出现的才压入队列
p.push(h);
}
}
return -1;
}
int main(){
ll x,k=8;
cin>>x;
while(x){
st[k--]=x%10;
x/=10;
}
ll anss=bfs();
cout<<anss<<endl;
return 0;
}
二、双向bfs
同时从起点和终点向对方做bfs,将在中间的某个位置相遇,此时即得到了最优路径。双向广搜的应用场合是知道起点,终点,并且正向和逆向都能进行搜索。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int dx[]={1,0,0,-1};
int dy[]={0,1,-1,0};
int st[9];
int goal[]={1,2,3,8,0,4,7,6,5};
int fuc[]={1,1,2,6,24,120,720,5040,40320,362880};
int mp[10000000];
int mq[10000000];
struct node{
int s[9];
int step;
};
queue<node>p;
queue<node>q;
ll cantor(int a[]){
ll ans=0;
for(int i=0;i<9;i++){
int z=0;
for(int j=i+1;j<9;j++)
if(a[j]<a[i])
z++;
ans+=fuc[8-i]*z;
}
return ans;
}
ll bfs(){
node t;
node t2;
memcpy(t.s,st,sizeof(t.s));
t.step=0;
if(memcmp(t.s,goal,sizeof(goal))==0)//特判,起点即为终点时
return t.step;
memcpy(t2.s,goal,sizeof(t2.s));
t2.step=0;
p.push(t);
q.push(t2);
while(!p.empty()||!q.empty()){
int z,z2;
if(p.size()<q.size()){
t=p.front();
p.pop();
for(int i=0;i<9;i++){
if(t.s[i]==0)
z=i;
}
int x=z%3;
int y=z/3;
for(int i=0;i<4;i++){
int nx=x+dx[i];
int ny=y+dy[i];
if(nx<0||nx>2||ny<0||ny>2)
continue;
node h;
memcpy(&h,&t,sizeof(struct node));
swap(h.s[y*3+x],h.s[ny*3+nx]);
++h.step;
ll sum=cantor(h.s);
if(!mp[sum]){
p.push(h);
mp[sum]=h.step;
}
if(mp[sum]&&mq[sum]){
return mp[sum]+mq[sum];
}
}
}
else{
t2=q.front();
q.pop();
for(int i=0;i<9;i++){
if(t2.s[i]==0)
z2=i;
}
int x2=z2%3;
int y2=z2/3;
for(int i=0;i<4;i++){
int nx=x2+dx[i];
int ny=y2+dy[i];
if(nx<0||nx>2||ny<0||ny>2)
continue;
node h;
memcpy(&h,&t2,sizeof(struct node));
swap(h.s[y2*3+x2],h.s[ny*3+nx]);
h.step++;
ll sum=cantor(h.s);
if(!mq[sum]){
q.push(h);
mq[sum]=h.step;
}
if(mp[sum]&&mq[sum]){
return mp[sum]+mq[sum];
}
}
}
}
}
int main(){
int x,k=8;
cin>>x;
while(x){
st[k--]=x%10;
x/=10;
}
ll anss=bfs();
cout<<anss<<endl;
return 0;
}
三、A*算法
在搜索过程中,用一个评估函数对当前情况进行评估,得到最好的状态,从这个状态继续搜索,直到目标。设x是当前所在状态,f(x)是对x的评估函数,有 f(x)=g(x)+h(x)
g(x):表示从初始状态到现在状态(x)的代价;
h(x):表示从现在状态(x)到终点的最优路径的评估。(abs(a.x-x2)+abs(a.y-y2))*10;(曼哈顿距离,x2,y2表示终点坐标。a表示当前点)
A*算法的具体步骤:
1.把起点加入openlist(开启列表,一般是一个优先队列)
2.遍历openlist ,找到F值最小的节点,把它作为当前处理的节点,并把该节点加入closelist(关闭列表,可以开个数组表示)中
3.对该节点的8个相邻格子进行判断,如果格子是不可抵达的或者在closelist中,则忽略它,否则如下操作:
a. 如果相邻格子不在openlist中,把它加入,并将parent设置为该节点和计算f,g,h值
b.如果相邻格子已在openlist中,并且新的G值比旧的G值小,则把相邻格子的parent设置为该节点,并且重新计算f值。
重复2,3步,直到终点加入了openlist中,表示找到路径;或者openlist空了,表示没有路径。
最后从目标格开始,沿着每一格的父节点移动直到回到起始格,这就是路径。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int dx[]={1,0,0,-1};
int dy[]={0,1,-1,0};
int goal[]={1,2,3,8,0,4,7,6,5};
int fuc[]={1,1,2,6,24,120,720,5040,40320,362880};
int st[9];
int vis[1000000];//关闭列表
int po[1000000];
struct node{
int step;
int f;
int s[9];
bool operator < (const node &x) const { //在优先队列里按f的大小排序
return f > x.f;
}
};
struct hh{
int x;
int y;
}mp[10000];
priority_queue<node>q;//开启列表
ll cantor(int a[]){
ll ans=0;
for(int i=0;i<9;i++){
int k=0;
for(int j=i+1;j<9;j++){
if(a[i]>a[j])
k++;
}
ans+=k*fuc[8-i];
}
return ans;
}
//启发函数h为所有数字离正确位置的曼哈顿距离.
ll h(int cur[]){
int res = 0;
for (int i = 0; i < 9; i ++ ){
if (goal[i] != cur[i] && goal[i] != 0) res++;
}
return res;
}
ll axing(){
node t;
t.step=0;
memcpy(t.s,st,sizeof(st));
t.f=h(t.s);
q.push(t);
vis[cantor(t.s)]=1;
while(!q.empty()){
t=q.top();
q.pop();
if(memcmp(t.s,goal,sizeof(goal))==0)
return t.step;
int z;
for(int i=0;i<9;i++){
if(t.s[i]==0)
z=i;
}
int x=z%3;
int y=z/3;
for(int i=0;i<4;i++){
int nx=x+dx[i];
int ny=y+dy[i];
if(nx<0||nx>2||ny<0||ny>2)
continue;
node he;
memcpy(&he,&t,sizeof(struct node));
swap(he.s[y*3+x],he.s[ny*3+nx]);
ll sum=cantor(he.s);
if(!vis[sum]||(vis[sum]&&(he.step+1)<po[sum])){
po[sum]=he.step+1;
he.f=h(he.s)+he.step+1;
he.step++;
q.push(he);
vis[sum]=1;
}
}
}
}
int main(){
int x,k=8;
cin>>x;
while(x){
st[k--]=x%10;
x/=10;
}
for(int i=0;i<9;i++){
int xx=i%3;
int yy=i/3;
mp[goal[i]].x=xx;
mp[goal[i]].y=yy;
}
ll anss=axing();
cout<<anss<<endl;
return 0;
}