数据结构-归并排序+计数排序
1.归并排序
基本思想:
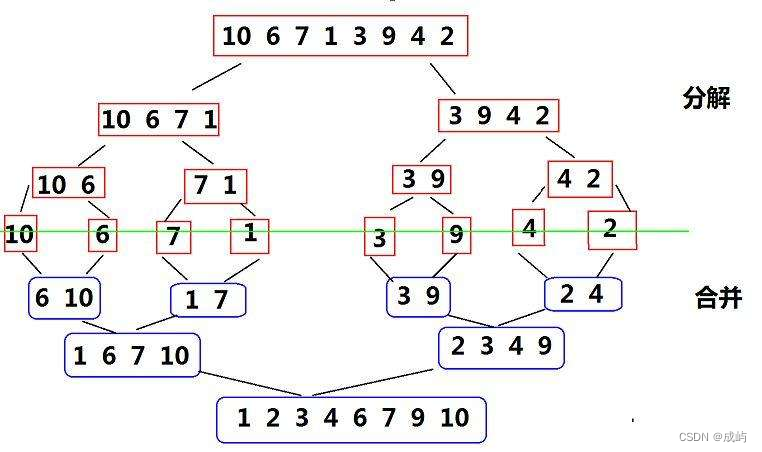
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
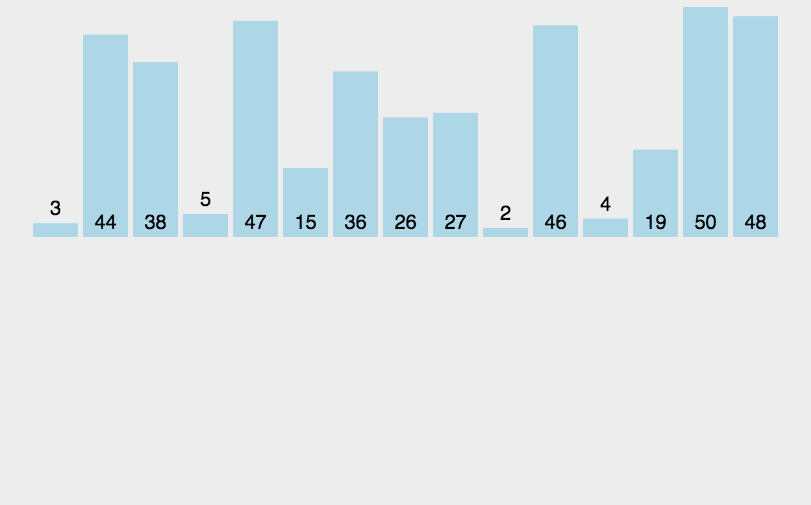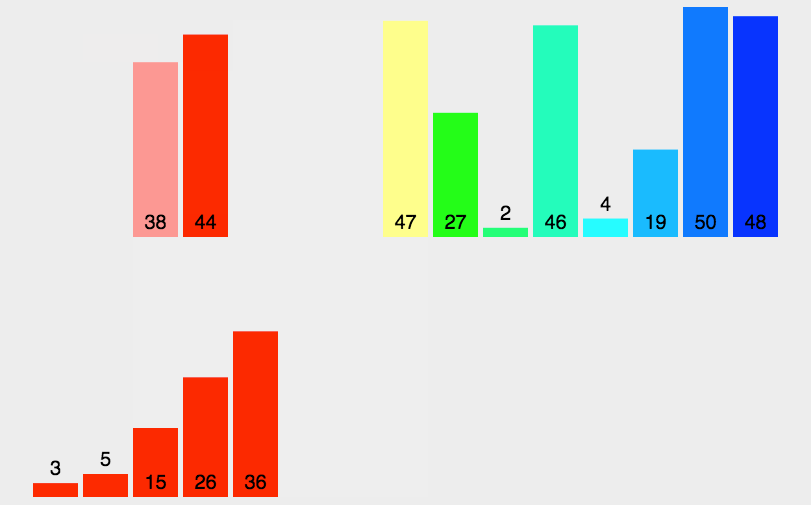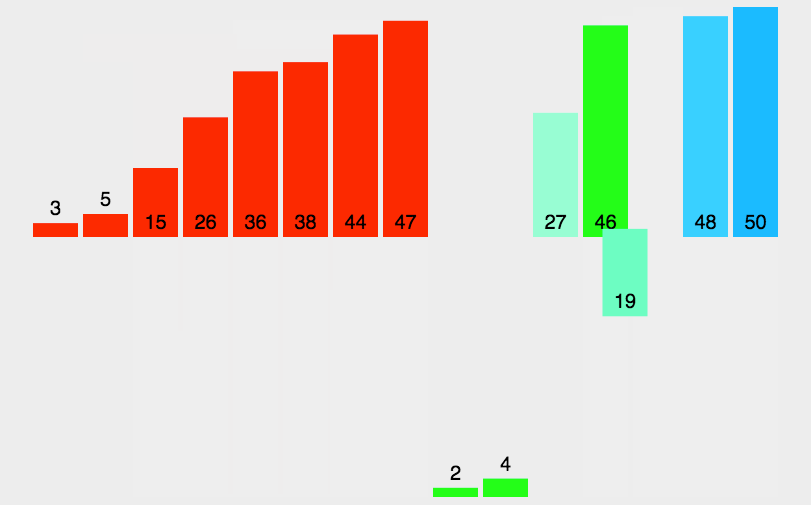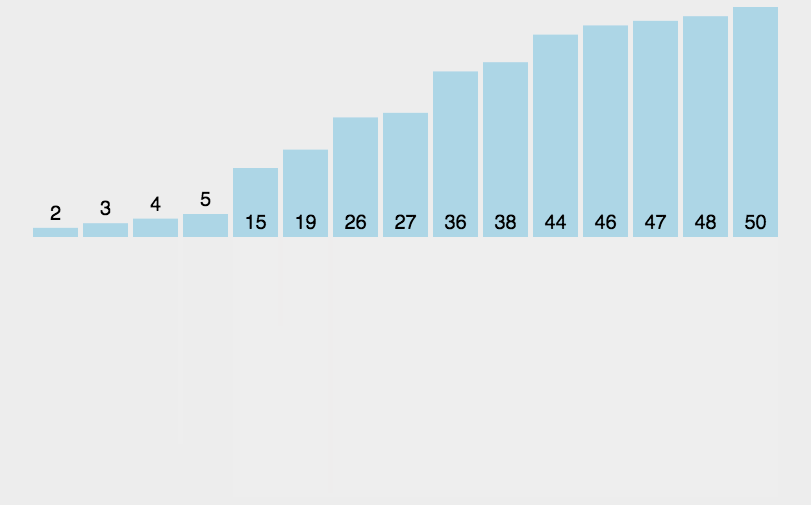
相当于每次把待排数据分为两个子区间,如果每个子区间有序,再让两个子区间归并起来也有序,那整体就有序了。我们可以按照二叉树的思想,把子区间再分为两份,使子区间的子区间有序.......直到子区间分无可分为止。
具体过程如下:
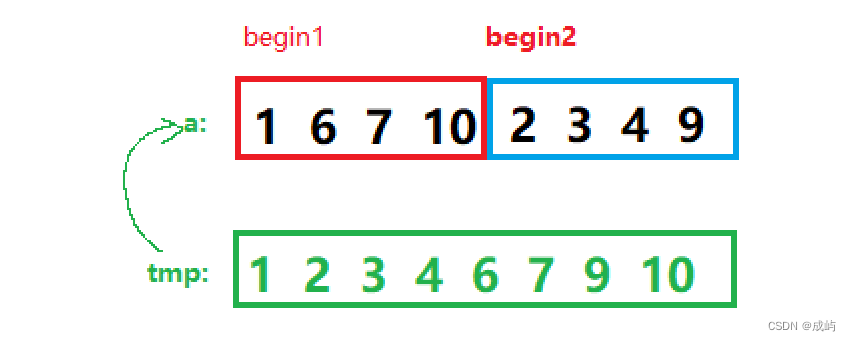
那该如何让两个有序子区间归并呢?
直接在数组中肯定不行,这样会发生数据的覆盖。所以我们可以像之前合并两个有序数组一样,另外开辟一个空间tmp,依次比较两个有序子区间的值,每次比较后把较小的放在tmp中,如果其中一个子区间提前结束,就把另外一个子区间的剩余的数据全放进tmp,最后把tmp中的数据拷贝回原数组。
使用递归实现:
#include<stdio.h> #include<stdlib.h> void _MegeSort(int* a, int begin, int end,int*tmp) { //只剩一个数据,递归结束 if (begin == end) { return; } int mid = (begin + end) / 2; //递归子区间,分为两部分 _MegeSort(a, begin, mid, tmp); _MegeSort(a, mid+1, end, tmp); int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int j = begin; //两部分比较,每次小的放入tmp while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } //哪部分有剩余,全部放入tmp while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } //拷贝到原数组 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } void MegeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); _MegeSort(a, 0, n - 1, tmp); free(tmp); } void Print(int* a, int n) { for (int i = 0; i < n; i++) { printf("%d ",a[i]); } printf("\n"); } int main() { int a[] = { 1,4,9,6,3,5,2,8,10,7,11,1}; MegeSort(a, sizeof(a) / sizeof(int)); Print(a, sizeof(a) / sizeof(int)); return 0; }注意:
1. 因为每次递归的子区间都不一定是从0开始的,所以我们拷贝数据时,最好从begin的位置开始:
//拷贝到原数组 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));2. 在代码中j作为tmp的坐标,每次往tmp中放入数据后都要加一,但不能初始化为0,否则每次递归进入,j的值都会清0,所以最好初始化:j=begin
归并排序的复杂度:
时间复杂度:O(N*logN)
归并排序每次递归都要把待排数据分为两份,相当于二分法,那一共有logN层递归,而每次递归都要比较数据,要把每个数据都遍历一遍,每层的时间复杂度就是O(N),所以总共的时间复杂度是O(N*logN)。
空间复杂度:O(N)
刚开始就开辟了空间,此时就已经是O(N)了,而递归过程中函数栈帧的创建是logN,所以总的空间复杂度是:O(N+logN),但是量级没变,还是O(N)。
2.非递归实现归并排序
非递归实现归并排序,我们只需模拟上述的递归过程即可,把递归过程转换为:把数据先分为2个一组,全部归并一遍,拷贝回原数组,然后4个一组,全部归并一遍,拷贝回原数组,再8个一组, 全部归并一遍,拷贝回原数组,
那我们就可以设置一个gap,两个数据为一组时,gap=1,每归并一组数据就往后跳2*gap步,直到全部归并一遍,再次分组,这次gap=2,每归并一组数据往后跳2*gap步,直到全部归并一遍,下次gap=4,跳2*gap步.....,直到gap>n就停止,
代码如下:
void MegeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail\n"); return; } int gap = 1; while (gap < n) { int j = 0; for (int i = 0; i < n; i += 2 * gap) { int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //两部分比较,每次小的放入tmp while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } //哪部分有剩余,全部放入tmp while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } } memcpy(a, tmp, sizeof(int) * n); gap *= 2; } free(tmp); }测试一下:
上面结果看起来,我们排序成功了,但是上述代码真的对吗?
上面代码我们在测试时用的是8个数据,但是如果用9个、10个等,就会发现排序并不会成功,可能程序还会崩掉,这是为什么呢?
因为我们在分组时,是按照固定的2的次方分的,一旦数据个数不是2、4、8的次方,后面归并时就会发生越界问题。
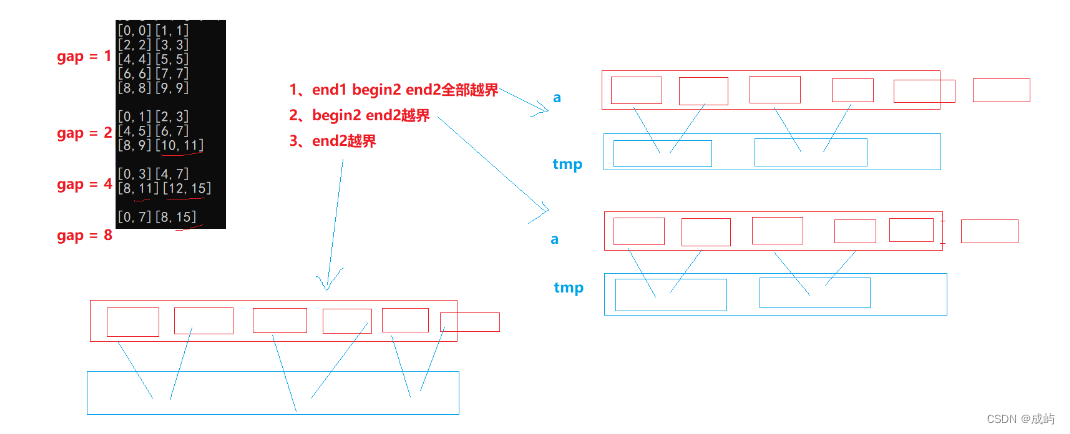
下面我们给10个数据打印一下边界,会发现,有三种越界的方式,:
那我们对这三种情况分别做一下处理:
第1、2种情况出现时,我们直接break,第三种情况,我们修改边界,令end2=n-1,但是注意直接break后,第1、2种情况往tmp中归并时会少一部分数据(如上图蓝框所示),所以最后把tmp的数据往a中拷贝时,不能一次性全部拷贝回去,否则a中这些数据就永远丢失了,所以最好归并一段,拷贝一段,这样拷贝过去的数据只会把前面的数据覆盖,没参与归并的数据还在a中。
代码如下:
void MegeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail\n"); return; } int gap = 1; while (gap < n) { int j = 0; for (int i = 0; i < n; i += 2 * gap) { int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; if (end1 >= n || begin2 >= n) { break; } //修正 if (end2 >= n) { end2 = n - 1; } //两部分比较,每次小的放入tmp while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } //哪部分有剩余,全部放入tmp while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } //归并一段,拷贝一段 memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1)); } gap *= 2; } free(tmp); }
3.计数排序
基本思想:
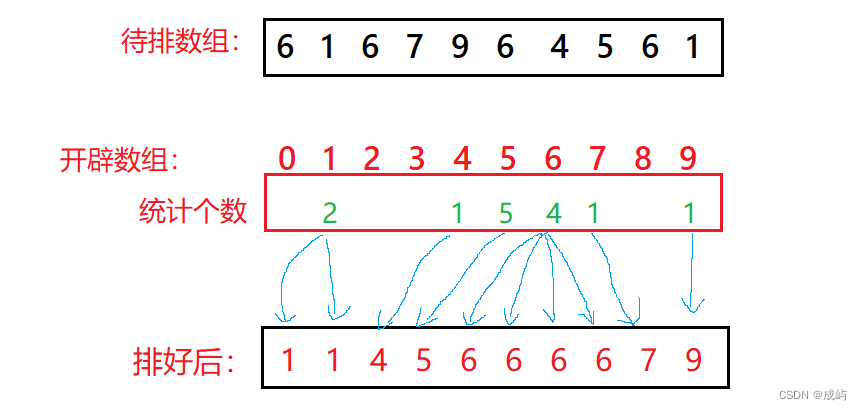
1. 统计每个数据出现的次数。
2. 根据数据的次数排序。
如果我们要排序的数在0~9之间,我们可以像上面一样开辟10个int大小的空间,统计待排数据中每个数据的个数,在开辟出的数组的相应下标处计数,那如果我们要排序的数据在100~109之间呢?难道开辟110个空间吗?
当然不是,我们可以做相对映射,在开辟空间之前,先找到待排数据中的最小值和最大值,开辟空间的大小就是:sizeof(int)*(max-min+1),开辟出的数组下标应该是:0~9,0~9下标的位置分别对应的是100~109,计数时,在下标为该数据减待排数据中的最小值的位置统计次数,例如:109就在109-100=9的下标处统计次数,统计完排序的时候再加上最小值即可。
代码如下:
#include<stdio.h> #include<stdlib.h> void CountSort(int* a, int n) { int min = a[0], max = a[0]; //找最大值和最小值 for (int i = 0; i < n; i++) { if (a[i] < a[0]) { min = a[i]; } if (a[i] > a[0]) { max = a[i]; } } int range = max - min + 1; int* count = (int*)malloc(sizeof(int) * range); memset(count, 0, sizeof(int) * range); //计数 for (int i = 0; i < n; i++) { count[a[i] - min]++; } //排序 int k = 0; for (int j = 0; j < range; j++) { while (count[j]--) { a[k++] = j + min; } } } //打印函数 Print(int* a, int n) { for (int i = 0; i < n; i++) { printf("%d ", a[i]); } printf("\n"); } int main() { int a[] = { 6,1,6,7,9,6,4,5,6,1 }; CountSort(a, sizeof(a) / sizeof(int)); Print(a, sizeof(a) / sizeof(int)); return 0; }
计数排序的复杂度:
时间复杂度:O(N+range)
寻找最大值和最小值时,遍历一遍数组,时间复杂度是:O(N),由于待排数据的范围是range,排序时所耗费的时间复杂度是:O(range),所以最终的时间复杂度是:O(N+range)
如果知道N和range的大小,N大,就是O(N),range大,就是O(range)。
空间复杂度:O(range)
额外开辟的空间个数是range,所以空间复杂度就是:O(range)
4.排序的复杂度和稳定性
总结如下:
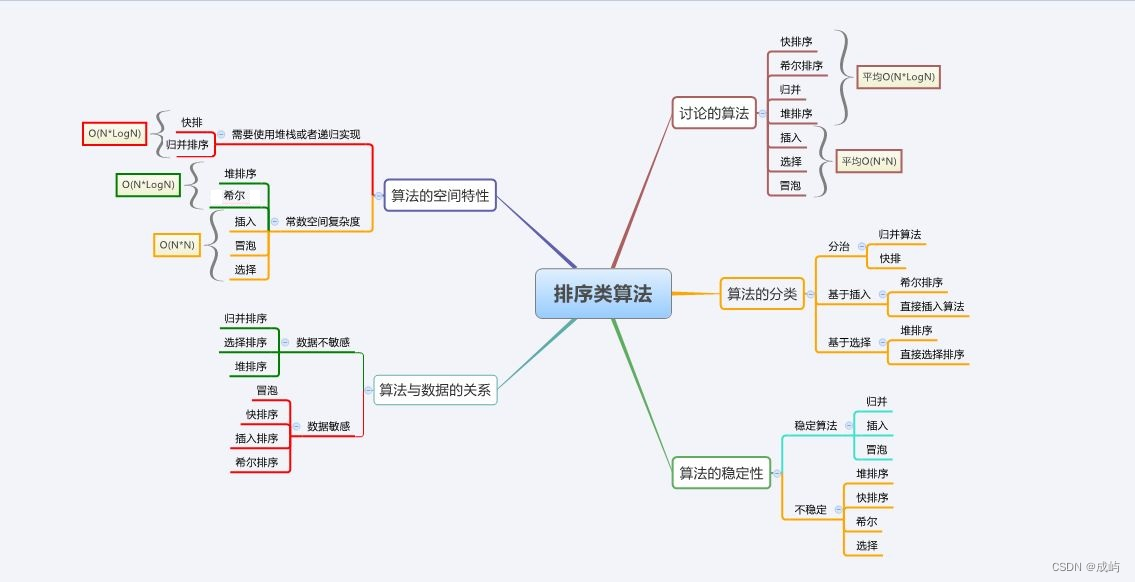
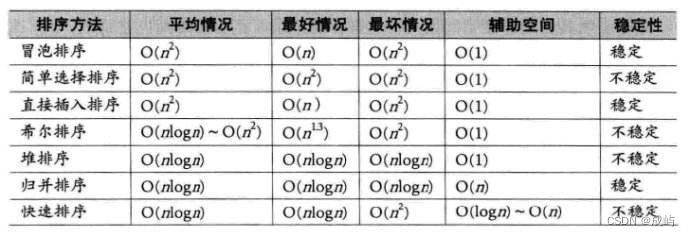
以上就是排序学习的全部内容了,到这,数据结构的学习就告一段落了,近期会停更一段时间,用来复习,后面将继续学习C++的知识,
未完待续。。。