基于知识获取共享的算法代码
基于知识获取共享的算法
gainesingsharing knowledge optimization algorithm (GSK)基于在人的生命周期内获取和共享知识的理念。它基于两个关键因素阶段:
- 第一阶段称为初-中级或初级获取与分享阶段;
- 第二阶段称为中级-专家或高级获取与分享阶段;
下面将分别描述这两个阶段。
事实上,特定人群中的所有个体(人)可以在一起互动,他们通过合作和竞争不断影响彼此,以非常有经验和足够资格处理现实生活中的情况解决复杂的问题。然而,作为一个有经验的人,你必须从别人那里获得和分享知识。因此,人类寿命期间,每个人在一个特定的人口增长知识在早期阶段(早中)获得知识通过不同类型的非常小的网络如他她(家人、邻居、亲戚)比获得更现实的等不同类型的更大的网络(工作、社会朋友和许多其他人)。
此外,由于经验有限,这一阶段的知识来源很少,他/她仍然希望与其他不同类型的人分享他的观点,想法和技能,可能在小的网络之外。事实上,在这个阶段,他必须考虑到,他没有足够的资格,生活经验很少,以区分和分类不同类型的人,不属于他她的小网络,好人和坏人。
另一方面,在(中后期)年阶段,由于与更大的网络(如同事、社交媒体上的朋友和其他人)互动,每个人都有自己的不同领域的知识,可以显著改善获得它从别人主要是派生按照领导人的成功,相信在精英人士的意见除了避免失败的人或激进的概念或糟糕的性能在各个领域。事实上,在这个阶段,每个人都有很强的判断、思考和把不同类型的人分为好、中、坏的等级的能力。因此,他可以很容易地将自己在不同领域的知识和经验分享给最合适、性格和行为良好的人(即从他们的知识和经验中获益)。对上述知识获取-共享概念的数学解释如下。
让
x
i
=
1
,
2
,
3
,
…
,
N
x_i= 1,2,3,…,N
xi=1,2,3,…,N的人一个特定的人口,也就是说,这个人口包含N人每个人喜被定义为
x
i
j
=
(
(
ξ
1
,
ξ
2
)
,
…
,
x
i
D
)
x_{ij} =((ξ_1,ξ_2),…,x_{iD})
xij=((ξ1,ξ2),…,xiD),
D
D
D是分配给一个人的学科领域的数量,也就是决定一个人的维度的知识分支和
f
i
f_i
fi,
i
=
1
,
2
,
…
,
N
i = 1,2,…,N
i=1,2,…,N分别为对应的适应度值。因此,显然它可以推导出从图6的主要思想是在初中获得和分享阶段(含早阶段)每个向量的维数(改变)被另一个值将替代使用初级获取-共享方案不仅仅是更新的数量维度使用高级获得和共享方案即数量使用初级增益共享规则的更新维数大于使用高级增益共享规则的更新维数。
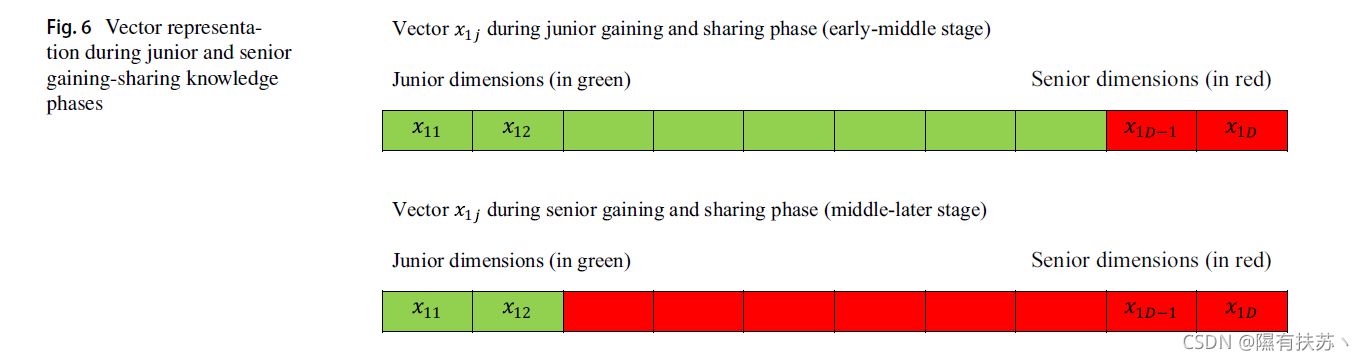
但在高级阶段(中后期),采用高级增益共享方案的每个向量的更新维数大于采用初级增益共享方案的每个向量的更新维数。此外,必须考虑到使用初级和高级阶段替换的所需维度数量取决于情况:
D ( j u n i o r p h a s e ) = ( p r o b l e m s i z e ) ∗ ( 1 − G / G E N ) k D(juniorphase)=(problemsize)*(1-G/GEN)^k D(juniorphase)=(problemsize)∗(1−G/GEN)k
其中 k k k为知识率,并且 k > 0 k>0 k>0, G G G为代数, G E N GEN GEN为最大代数:
D ( s e n i o r p h a s e ) = p r o b l e m s i z e − D ( j u n i o r p h a s e ) D(seniorphase) = problemsize − D(juniorphase) D(seniorphase)=problemsize−D(juniorphase).
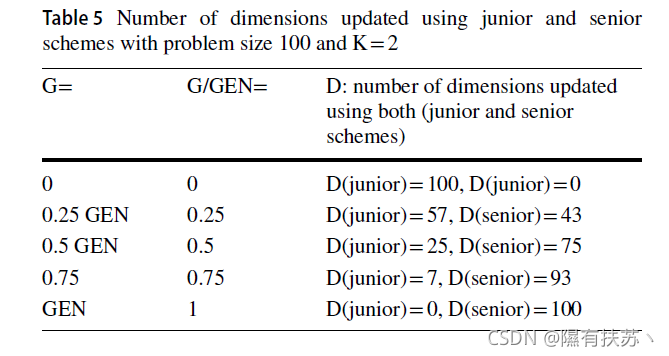
因此,使用两种方案的每个向量获得的和共享的维数将在初始化阶段确定。为了进一步说明,假设问题大小为100,
k
k
k为2。因此,这个方程在增长速率中减小(表5)。
显然,知识率
k
k
k通过使用控制每个个体世世代代的经验速率。计划(由初级阶段至高级阶段)。
- 当 k = 1 k =1 k=1时,它是线性的减少和增加,即使用初级方案的更新维数是线性的减少,而使用高级方案的更新维数是线性的增加,否则分别是非线性的减少和增加。
- 当 k ∈ ( 0 , 1 ) k∈(0,1) k∈(0,1),使用初级方案更新的维数会缓慢地(非线性地)减少。因此,在生成过程中,初级方案的应用比高级方案多,这意味着在不同的知识分支中获得经验的速度较慢。另一方面,
- 当 k > 1 k>1 k>1、使用初级格式更新的维数迅速(非线性)减少。因此,在代中,高级方案的使用次数会多于初级方案,这意味着在不同的知识分支中获得经验的速度会更快。
初级知识获取分享阶段
在这个阶段,每个试图获得知识从最近的和值得信赖的个人,属于小团体,而他也试图分享知识和一些人不属于,或不是在任何集团成员由于他的好奇心和探索欲望。
因此,使用初级方案计算每个个体的更新情况如下:
- 根据目标函数值将所有个体按升序排列: x b e s t , . . . . . . , x i − 1 , x i , x i + 1 , . . . . . . x w o r s t x_{best},......, x_{i−1},x_i, x_{i+1},......x_worst xbest,......,xi−1,xi,xi+1,......xworst
- 然后,对于每个个体
x
i
x_i
xi,选择两个不同的个体(最接近的个体),最接近的较好个体
x
i
−
1
x_{i−1}
xi−1和较差个体
x
i
+
1
x_{i+1}
xi+1构成知识获取源。另外,随机选择另一个个体
x
r
x_r
xr作为知识共享的来源。初级知识获取-共享阶段伪代码如图7所示。

注意:在这个阶段,最好的和最差的个体分别通过使用最近的最好的两个个体和最近的恶化的两个个体来更新。
如果xi是全局最优,则选择最近的两个最优个体如下:
x
b
e
s
t
,
x
b
e
s
t
+
1
,
x
b
e
s
t
+
2
)
x_{best}, x_{best+1}, x_{best+2)}
xbest,xbest+1,xbest+2)。
如果xi是全局最差的,选择最接近的前使两个个体恶化如下:
.
.
.
.
.
.
.
.
.
x
w
o
r
s
t
−
2
,
x
w
o
r
s
t
−
1
,
x
w
o
r
s
t
... ... ... x_{worst−2},x_{worst−1},x_{worst}
.........xworst−2,xworst−1,xworst。
其中
k
f
>
0
k_f>0
kf>0. 这是(知识因素)控制的总数量获得和共享的知识,将从其他人添加到当前的个人在几代。
其中
k
r
∈
[
0
,
1
]
k_r∈[0,1]
kr∈[0,1]。是(知识比率)控制了将在几代人之间传递(继承)的获得和共享知识的总量(当前经验和获得经验之间的比率)。
高级获取共享知识阶段
这一阶段涉及利用特定人口中不同类别的人,即最好的、较好的和最坏的人的现有资料和适当知识。利用是指他人(好人和坏人)对一个人的影响和影响。因此,每个人的更新可以使用高级计划计算如下:
- 将所有个体按其目标函数升序排序后,将其分为最佳个体、较好或中等个体、最差个体三类。
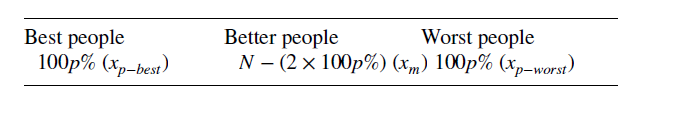
- 为每个单独的
x
i
x_i
xi,提出高级计划使用两个随机选择的向量的顶部和底部100 p %个体在当前人口规模
N
P
NP
NP 形式获得的部分,而选择第三个向量随机从中间N−(2×100 p %)个人形式分享的部分。图8给出了高级获取-共享知识阶段伪代码。
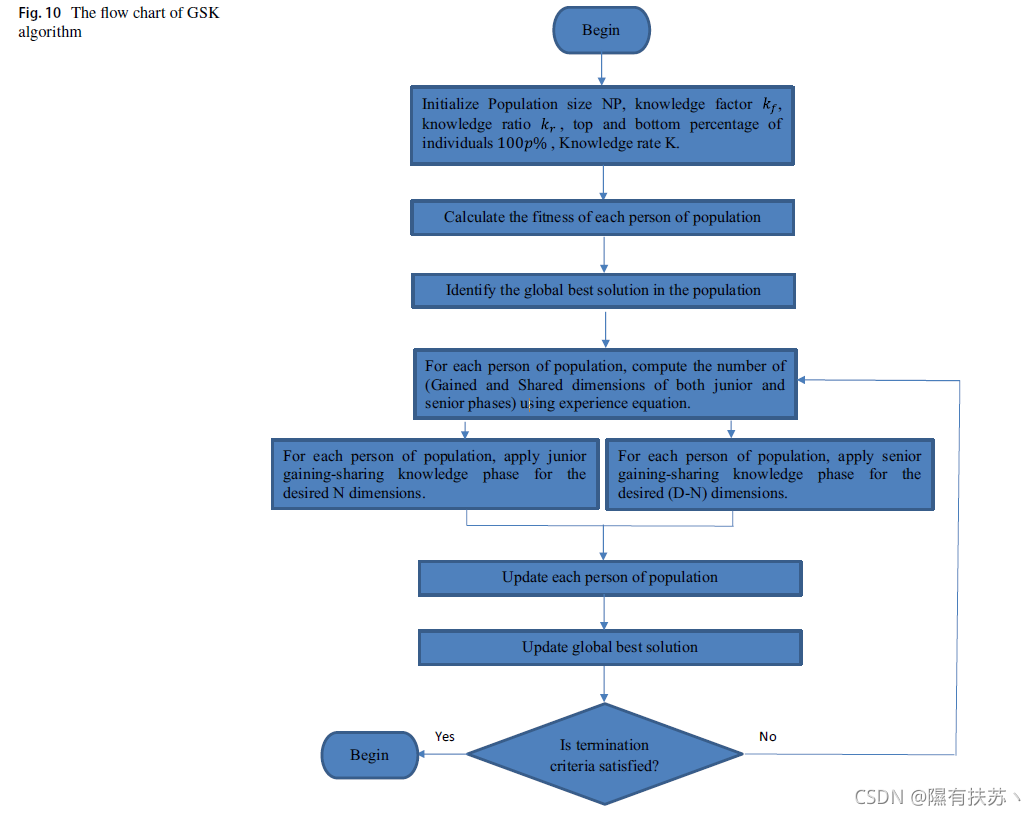
其中 p ∈ [ 0 , 1 ] p∈[0,1] p∈[0,1],且 p = 0.1 p = 0.1 p=0.1, NP的10%是合适的。GSK算法的伪代码和流程图分别如图9和10所示。


MATLAB代码
function [X_best,Best_fit,All_fit,nfes,res_det]= APGSK_IMODE(max_nfes,L,H,func_num,D,fhd,C,Par,Run_No)
load Rand_Seeds Rand_Seeds
rng(D*func_num*Rand_Seeds(Run_No),'twister');
% Rand_Seeds=load('input_data\Rand_Seeds.txt');
% seed_ind=(D/10*func_num*30+Run_No)-30;
% seed_ind=mod(seed_ind,1000);
% run_seed=Rand_Seeds(seed_ind);
% rng(run_seed,'twister');
D=Par.n;
lu = [L * ones(1, D); H * ones(1, D)];
NP=Par.PopSize;
max_NP = NP;
min_NP = 12.0;
min_NP1=4;
Pop = repmat(lu(1, :), NP, 1) + rand(NP, D) .* (repmat(lu(2, :) - lu(1, :), NP, 1));
Fit=feval(fhd,Pop',func_num,C);
nfes = NP;
Fit=Fit';
[~,I_best]=min(Fit);
X_best=Pop(I_best,:);
res_det= min(repmat(min(Fit),Par.PopSize,1), Fit); %% used to record the convergence
PS2=NP/4;
PS1=NP-PS2;
% PS2=NP-PS1;
max_NP1=PS1;
max_NP2=PS2;
%% ================== fill in for each Algorithm ===================================
%% IMODE
EA_1= Pop(1:PS1,:); EA_obj1= Fit(1:PS1);
%% APGSK
EA_2= Pop(PS1+1:size(Pop,1),:); EA_obj2= Fit(PS1+1:size(Pop,1));
%% ===================== archive data ====================================
arch_rate=1.4;
archive.NP = arch_rate * PS1; % the maximum size of the archive
archive.pop = zeros(0, Par.n); % the solutions stored in te archive
archive.funvalues = zeros(0, 1); % the function value of the archived solutions
%% APGSK setting
%%POSSIBLE VALUES FOR KNOWLEDGE RATE K%%%%
EA_1old=EA_1;
hist_pos=1;
memory_size=15*Par.n;
archive_f= ones(1,memory_size).*0.5;
archive_Cr= ones(1,memory_size).*0.5;
archive_T = ones(1,memory_size).*0.1;
archive_freq = ones(1, memory_size).*0.5;
F = normrnd(0.5,0.15,1,NP);
cr= normrnd(0.5,0.15,1,NP);
probDE1=1./Par.n_opr .* ones(1,Par.n_opr);
[bestold, bes_l]=min(Fit); bestx= Pop(bes_l,:);
Probs=[1 1];
it=0;
cy=0;
stop_con=0;
while stop_con==0 % nfes<max_nfes
it=it+1;
cy=cy+1; % to control CS
% ================ determine the best phase ===========================
if(cy==ceil(Par.CS+1))
%%calc normalized qualit -- NQual
qual(1) = min(EA_obj1);
qual(2) = min(EA_obj2);
norm_qual = qual./sum(qual);
norm_qual=1-norm_qual; %% to satisfy the bigger is the better
Probs=norm_qual;
%%Update Prob_MODE and Prob_CMAES
Probs = max(0.1, min(0.9,Probs./sum(Probs)));
[~,indx]=max(Probs);
if Probs(1)==Probs(2)
indx=0;%% no sharing of information
end
if indx>0
Probs=[0 0];
Probs(indx)=1;
end
elseif cy==2*ceil(Par.CS)
%% share information
if indx==1
EA_2(PS2,:)=EA_1(1,:);
EA_obj2(PS2)=EA_obj1(1);
[EA_obj2, ind]=sort(EA_obj2);
EA_2=EA_2(ind,:);
else
if (min (EA_2(1,:)))> -100 && (max(EA_2(1,:)))<100 %% share best sol. in EA_2 if it is feasible
EA_1(PS1,:)= EA_2(1,:);
EA_obj1(PS1)= EA_obj2(1);
[EA_obj1, ind]=sort(EA_obj1);
EA_1=EA_1(ind,:);
end
end
%% reset cy and Probs
cy=1; Probs=ones(1,2);
end
if (rand<=Probs(1))
%% apply IMODE
[EA_1, EA_1old, EA_obj1,probDE1,bestold,bestx,archive,hist_pos,memory_size, archive_f,archive_Cr,archive_T,archive_freq, nfes,F,cr, res_det] = ...
IMODE( EA_1,EA_1old, EA_obj1,probDE1,bestold,bestx,archive,hist_pos,memory_size, archive_f,archive_Cr,archive_T,....
archive_freq, Par.xmin, Par.xmax, Par.n, PS1, nfes, func_num,Par.Printing,Par.max_nfes, Par.Gmax,F,cr,C,fhd,res_det);
if(~isempty(Par.Record_FEs))
if (nfes>=Par.Record_FEs(1))
Par.All_fit=[Par.All_fit;min(EA_obj1)];
Par.Record_FEs(1)=[];
end
end
if nfes >= max_nfes
[Best_fit,I_best]= min(EA_obj1);
X_best=EA_1(I_best,:);
All_fit=Par.All_fit;
return;
end
plan_NP1 = round((((min_NP1 - max_NP1) / (max_nfes)) * nfes) + max_NP1);
% UpdPopSize = round((((Par.MinPopSize - InitPop) / Par.Max_FES) * current_eval) + InitPop);
Par.p_best_rate = (((Par.p_best_rate_min - Par.p_best_rate_max) / (max_nfes)) * nfes) + Par.p_best_rate_max;
if PS1 > plan_NP1
reduction_ind_num = PS1 - plan_NP1;
if PS1 - reduction_ind_num < min_NP1
reduction_ind_num = PS1 - min_NP1;
end
PS1 = PS1 - reduction_ind_num;
for r = 1 : reduction_ind_num
[valBest, indBest] = sort(EA_obj1, 'ascend');
worst_ind = indBest(end);
EA_1(worst_ind,:) = [];
EA_obj1(worst_ind,:) = [];
end
archive.NP = PS1;
if size(archive.NP, 1) > archive.NP
rndpos = randperm(size(archive.NP, 1));
rndpos = rndpos(1 : archive.NP);
archive.Pop = archive.Pop(rndpos, :);
end
end
end
if(rand<Probs(2))
%% Apply APGSK
[EA_2,EA_obj2,Par,nfes,res_det]= APGSK_fun(EA_2,EA_obj2,lu,func_num,Par,nfes,fhd,C,res_det);
if(~isempty(Par.Record_FEs))
if (nfes>=Par.Record_FEs(1))
Par.All_fit=[Par.All_fit;min(EA_obj2)];
Par.Record_FEs(1)=[];
end
end
if nfes >= max_nfes
[Best_fit,I_best]= min(EA_obj2);
X_best=EA_2(I_best,:);
All_fit=Par.All_fit;
return;
end
plan_NP2 = round((((min_NP - max_NP2) / (max_nfes)) * nfes) + max_NP2);
Par.p_best_rate = (((Par.p_best_rate_min - Par.p_best_rate_max) / (max_nfes)) * nfes) + Par.p_best_rate_max;
if PS2 > plan_NP2
reduction_ind_num = PS2 - plan_NP2;
if PS2 - reduction_ind_num < min_NP
reduction_ind_num = PS2 - min_NP;
end
PS2 = PS2 - reduction_ind_num;
for r = 1 : reduction_ind_num
[valBest, indBest] = sort(EA_obj2, 'ascend');
worst_ind = indBest(end);
EA_2(worst_ind,:) = [];
EA_obj2(worst_ind,:) = [];
Par.K(worst_ind,:)=[];
end
end
end
Fit=[EA_obj1;EA_obj2];
Pop=[EA_1;EA_2];
[Best_fit,I_best]= min(Fit);
X_best=Pop(I_best,:);
All_fit=Par.All_fit;
PopSize=size(Pop,1);
% res_det= [res_det; repmat(Best_fit,PopSize,1)];
% fprintf('current_eval\t %d fitness\t %d \n', nfes, Best_fit);
if (nfes>=Par.max_nfes)
stop_con=1;
end
if ( (abs (Par.f_optimal - Best_fit)<= 1e-8))
stop_con=1;
end
end
end
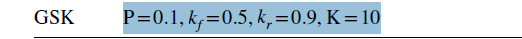
实验
为了评估算法的性能,在测试套件上进行了实验。我们采用求解误差测度(f (x) f (x)),其中x是算法一次运行得到的最佳解,x*是每个基准函数众所周知的全局最优解。误差值和小于10 8的标准偏差为零[140]。对于CEC2017,函数的尺寸(D)分别为10、30、50和100。将最大函数评估数(FEs),即终端标准,设置为10,000 D,每个函数和每个算法的所有实验都独立运行51次。对于CEC2011来说,问题有不同的维度[141]。最大函数评估数(FEs),即终端标准,设置为150,000,每个函数和每个算法的所有实验都独立运行25次。GSK与相关文献中10种最先进的基于人群的算法进行了比较。这些算法有:TLBO [137], GWO [80], SFS [18], AMO [78], DE [11], BBO [51], ACO [21], ES [30], GA [6], PSO[24]。上述算法的控制参数如表6所示。注意,所有算法的控制参数都直接取自它们的原始参考文献。据我们所知,这是第一个使用所有方法的研究这些不同类型的方法对最新的基准问题进行评价和比较。为了进行综合评价,实验结果的展示分为两个小节。首先,讨论了该算法的性能。其次,将GSK与其他10种最先进的算法进行整体性能比较。不同算法的性能评估基于最近为CEC 2017比赛定义的评分指标[140]。因此,每个算法的评价方法是基于100分,这是基于以下两个标准,考虑到更高的维度将给予更高的权重:


注意f2已经被排除在外,因为它表现出不稳定的行为,特别是在高维空间。从统计的角度对不同算法的求解质量进行比较和分析,并对其进行检验随机算法的行为,结果比较使用非参数统计假设检验:多问题Wilcoxon符号秩检验(检查所有算法对所有函数的差异);在0.05的显著性水平,R +表示测试问题的秩和第一个算法执行比第二个算法(在第一列),和R代表了秩次的测试问题第一个算法执行比第二个算法(在第一列)。级别越大,表现差异越大。作为零假设,假设两个样本的均值结果之间没有显著性差异。而另一种假设是两个样本的均值结果有显著性。对于CEC2017, D = 10、30、50、100维度的测试题数N = 29,显著性水平为5%。对于CEC2011,测试题数为22题,显著性水平为5%。使用p值与显著性水平进行比较。如果p值小于或等于显著性水平(5%),则拒绝原假设。本文所有的p值均使用SPSS (version 20.00)进行计算。