论文笔记:ICLR 2021 Combining Lable Propagation And Simple Models Out-Performs Graph Neural Network
前言:
本文的作者认为对于 GNN 的可解释性不足。基于此,作者在节点分类任务上提出可以通过将忽略图结构的浅层模型与两个利用标签结构中相关性的后处理方法相结合,超越或匹配最先进的 GNN 。具体如下:
(i)误差相关性:传播训练数据中的残余误差以纠正测试数据中的错误信息
(ii)预测相关性:在测试集数据上进行平滑预测
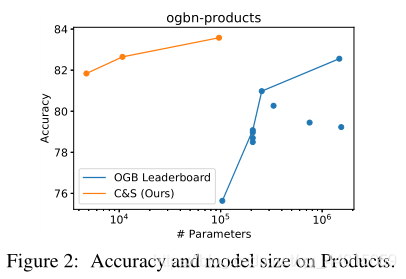
作者将整个过程称为 Correct and Smooth (C&S)。其中后处理步骤是通过对早期的基于图的半监督学习方法的标准标签传播方法进行修改实现的。该方法实现了惊人的性能提升,在 OGB-Products 数据集上使用比现有方法少137倍的参数量和100倍的训练时间达到了更佳的性能。
该方法的性能突出了如何直接将标签信息合并到学习算法(正如在传统技术中所做的那样)产生简单和实质性的性能增益。同时还可以将该技术整合到大型GNN模型中,提升模型性能。
论文链接:https://arxiv.org/abs/2010.13993
github:https://github.com/CUAI/CorrectAndSmooth
0. 标签传播算法
标签传播算法(label propagation)的核心思想非常简单:相似的数据应该具有相同的label。LP算法包括两大步骤:
1)构造相似矩阵;
2)标签传播。
0.1 相似矩阵构建
LP算法是基于Graph的,因此我们需要先构建一个图。我们为所有的数据构建一个图,图的节点就是一个数据点,包含labeled和unlabeled的数据。节点 i i i 和节点 j j j 的边表示他们的相似度。这个图的构建方法有很多,这里我们假设这个图是全连接的,节点 i i i 和节点 j j j 的边权重为:
w i j = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 α 2 ) (1) w_{ij}=exp(-\frac{||x_i-x_j||^2}{\alpha^2})\tag{1} wij=exp(−α2∣∣xi−xj∣∣2)(1)
其中
α
\alpha
α 作为超参
还有个非常常用的图构建方法是 knn 图,也就是只保留每个节点的
k
k
k 近邻权重,其他的为0,也就是不存在边,因此是稀疏的相似矩阵。
0.2 LP算法
标签传播算法非常简单:通过节点之间的边传播label。边的权重越大,表示两个节点越相似,那么label越容易传播过去。我们定义一个
N
×
N
N\times N
N×N 的概率转移矩阵
P
P
P :
P
i
j
=
P
(
i
→
j
)
=
w
i
j
∑
k
=
1
n
w
i
k
P_{ij}=P(i\rightarrow j)=\frac{w_{ij}}{\sum_{k=1}^nw_{ik}}
Pij=P(i→j)=∑k=1nwikwij
P
i
j
P_{ij}
Pij 表示从节点
i
i
i 转移到节点
j
j
j 的概率。假设有
C
C
C 个类和
L
L
L 个labeled样本,我们定义一个
L
×
C
L\times C
L×C 的label矩阵
Y
L
Y_L
YL,第
i
i
i 行表示第
i
i
i 个样本的标签指示向量,即如果第
i
i
i 个样本的类别是
j
j
j ,那么该行的第
j
j
j 个元素为1,其他为0。同样,我们也给
U
U
U 个unlabeled样本一个
U
×
C
U\times C
U×C 的label矩阵
Y
U
Y_U
YU。把他们合并,我们得到一个
N
×
C
N\times C
N×C 的soft label矩阵
F
=
[
Y
L
;
Y
U
]
F=[Y_L;Y_U]
F=[YL;YU]。
soft label的意思是,我们保留样本 i i i 属于每个类别的概率,而不是互斥性的,这个样本以概率1只属于一个类。当然了,最后确定这个样本 i i i 的类别的时候,是取max也就是概率最大的那个类作为它的类别的。那 F F F 里面有个 Y U Y_U YU,它一开始是不知道的,那最开始的值是多少?无所谓,随便设置一个值就可以了。
- 步骤1)就是将矩阵P和矩阵F相乘,这一步,每个节点都将自己的label以P确定的概率传播给其他节点。如果两个节点越相似(在欧式空间中距离越近),那么对方的label就越容易被自己的label赋予,就是更容易拉帮结派。
- 步骤2)非常关键,因为labeled数据的label是事先确定的,它不能被带跑,所以每次传播完,它都得回归它本来的label。随着labeled数据不断的将自己的label传播出去,最后的类边界会穿越高密度区域,而停留在低密度的间隔中。相当于每个不同类别的labeled样本划分了势力范围。
- 重复步骤1)和2)直到F收敛
1. Introduction
目前基于传统的 GNN 方法例如 GCN 和 GraphSAGE 的许多变体被提出用于有针对性地下游任务,大量的 GNN 方法选择在模型结构上进行改进来更好地建模语言信息或图片信息等,这导致了模型的可解释性变差同时无法适用于大型数据集。
因此作者以直推式图节点分类任务为基础,探究是否通过结合简单的模型来得到性能的提升,重点在于探索在图学习过程中的哪些地方可以容易的提升性能。
作者提出了一种模型框架:
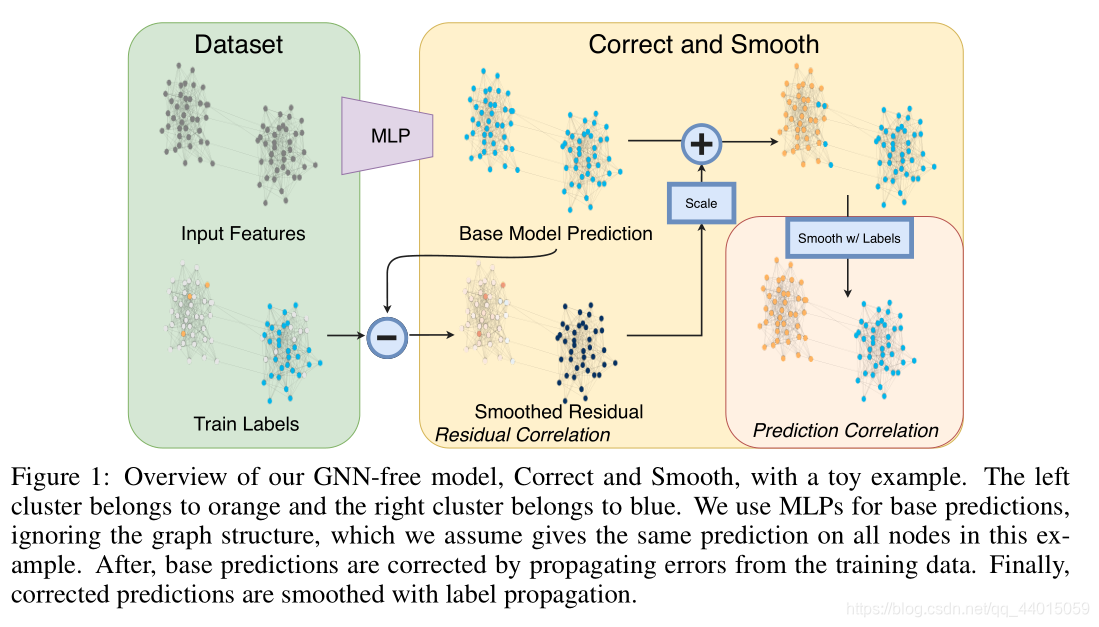
其中主要由三部分构成:
- 特征处理模块:忽略图结构信息,单纯通过节点特征完成任务,可以是 MLP 或线性模型
- 标签纠正模块:将训练数据中的不确定性传播到整个图中,以纠正特征处理模块的结果
- 预测平滑模块:对修正后的预测进行平滑处理得到最终结果
以该图为例,首先通过MLPs 进行基本预测,忽略了图结构,假设图结构在本例中对所有节点都给出了相同的预测(相同颜色的簇)。之后,通过传播训练数据中的错误来修正基本预测。最后,通过标签传播对修正后的预测进行平滑处理。
其中的标签纠正模块和预测平滑模块是传统的基于图的半监督学习方法,叫做标签传播。作者通过对原始方法进行修改在现有的 GNN 中达到了最佳的性能。在该框架中,图结构不是用来学习参数的,而是作为一种后处理机制。这种简单性使得模型具有更少的参数,训练所需的时间也更少,并且可以很容易地扩展到大型图。
作者分析能取得性能提升的主要原因是直接使用标签来进行预测,这些想法在很久之前就被提出,但是它们的出发点是是在点云数据上进行半监督学习,因此这些特征用来构建图。这之后,相关的技术被用来从标签中学习相关数据但是还没有将此应用于 GNN 的方法。也就是说作者发现,即使是简单的标签传播在很多的 benchmarks 上表现良好,这为组合两个模块来构建框架提供了理论基础:一个来自节点特征(忽略图结构),另一个来自在预测中直接使用已知标签。
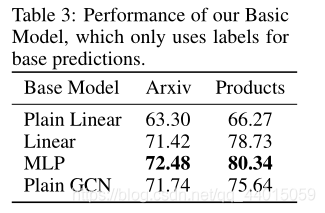
**此文的一个重要创新点在于从忽略图结构的模型中进行廉价的“基础预测”**来减少训练的资源消耗
总的来说,本文表明,结合几个简单的模型可以在直推式节点分类中产生优异的性能,而成本只占模型大小(即参数数量)和训练时间的一小部分。本文的目的并不是说目前的图学习方法很差或不合适。相反,我们的目标是突出一些更简单的方法,以提高图学习中的预测性能,并更好地理解性能收益的来源。本文的主要发现是,在学习算法中更直接地结合标签是关键。这是一项启发式的工作,希望该方法能激发新的想法,可以帮助其他图学习任务,如归纳节点分类、链接预测和图预测。
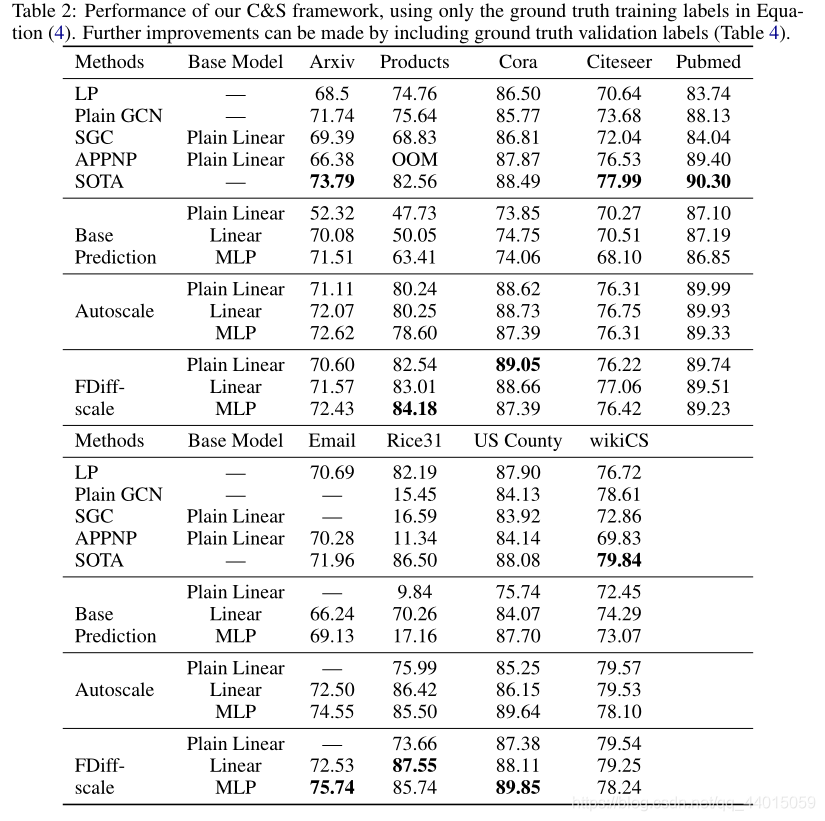
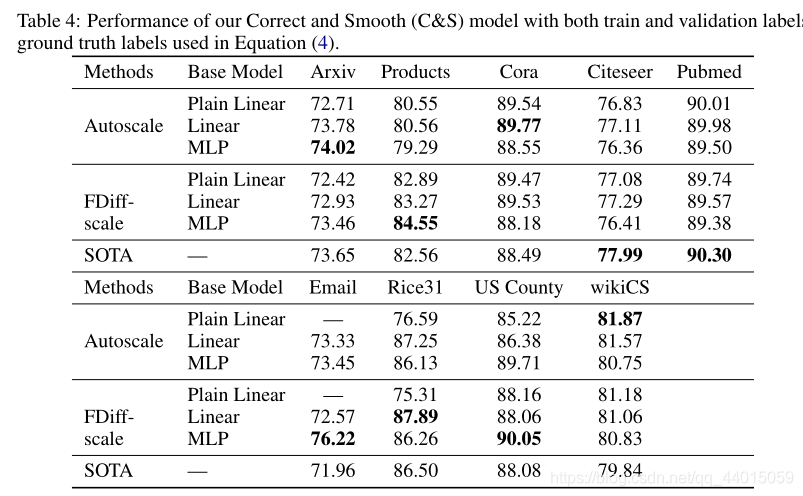
2. Correct And Smooth Model(C&S model)
对于半监督节点预测问题,节点集 V V V 被分为无标签节点集 U U U 和 有标签节点集 L L L。并且将标签表示为一个 one-hot 编码的矩阵 T ∈ R n × c T \in \mathbb{R}^{n \times c} T∈Rn×c 其中 n n n 代表节点的数量, c c c 代表标签的种类。进一步将有标签的节点集划分成训练集 L t L_t Lt 和 验证集 L v L_v Lv。最终的任务是,给出无向图 G G G,节点特征矩阵 X X X 和 节点标签矩阵 Y Y Y 来得到每一个节点的类别。 S = D − 1 2 A D − 1 2 S = D^{-\frac{1}{2}}AD^{-\frac{1}{2}} S=D−21AD−21 作为归一化的邻接矩阵。
该方法从一个简单的节点特征基础预测器开始,它不依赖于对图的任何学习。之后进行了两种类型的标签传播(LP):一种是通过建模相关误差修正基本预测,另一种是平滑最终预测。我们把这两种方法的结合称为正确的和平滑的(C&S)
LP只是后处理步骤也就是说该模型不是端到端的训练。此外,图仅用于这些后处理步骤和预处理步骤,以完成特征增强,但不用于基本预测。与标准的GNN模型相比,这使得训练速度更快,并且可扩展。
2.1 Simple Base Predictor
这里可以采用任意的表示学习模型例如线性模型和 MLP,就是一个单纯的特征学习过程。最终的基础预测 Z ∈ R n × c Z \in \mathbb{R}^{n \times c} Z∈Rn×c
2.2 Correcting For Error In Base Predictions With Residual Propagation
关键思想是期望基本预测中的误差沿着图中的边是正相关的。换句话说,节点 i i i 的错误会增加 i i i 的相邻节点发生类似错误的几率。因此应该尽可能在图中传播这种不确定性。该方法的灵感部分来自残差传播,其中类似的概念被用于节点回归任务,以及广义最小二乘和更广泛的相关误差模型。
为了实现此目的,作者定义了一个 错误矩阵
E
∈
R
n
×
c
E \in \mathbb{R}^{n \times c}
E∈Rn×c ,其中错误指的是训练集中的残差,对于验证集和无标签部分为 0
E
L
t
=
Z
L
t
−
Y
L
t
,
E
L
v
=
0
,
E
U
=
0
(2)
E_{L_t}=Z_{L_t}-Y_{L_t},E_{L_v}=0,E_U=0 \tag{2}
ELt=ZLt−YLt,ELv=0,EU=0(2)
只有当基本预测器做出完美预测时,对应训练节点的
E
E
E 行中的残差才为零。利用标签扩散技术对误差进行平滑处理,优化目标。
E
^
=
a
r
g
m
i
n
t
r
a
c
e
(
W
T
(
I
−
S
)
W
)
+
μ
∣
∣
W
−
E
∣
∣
F
2
,
W
∈
R
n
×
c
(3)
\hat{E}=argmintrace(W^T(I-S)W)+\mu||W-E||_F^2,W\in\mathbb{R}^{n\times c} \tag{3}
E^=argmintrace(WT(I−S)W)+μ∣∣W−E∣∣F2,W∈Rn×c(3)
该式的第一项鼓励在图上误差估计平滑,并且与 ∑ j = 1 c w j T ( I − S ) w j \sum_{j=1}^c w_j^T(I-S)w_j ∑j=1cwjT(I−S)wj 相等,其中 w j w_j wj 是矩阵 W W W 的第 j j j 行。第二项使解接近误差的初始猜测 E E E。解可以通过迭代过程 E ( t + 1 ) = ( 1 − α ) E + α S E ( t ) E^{(t+1)}=(1-\alpha)E + \alpha SE^{(t)} E(t+1)=(1−α)E+αSE(t),其中 α = 1 1 + μ \alpha = \frac{1}{1+\mu} α=1+μ1, E ( 0 ) = E E^{(0)}=E E(0)=E 迅速收敛得到。这种迭代是误差的扩散,我们将平滑的误差添加到基本预测中以得到修正的预测 Z ( r ) = Z + E ^ Z^{(r)} = Z +\hat{E} Z(r)=Z+E^。这是一种后处理技术,没有与基础预测相结合的训练。
这种类型的传播被证明是回归问题中高斯假设下的正确方法。然而,对于直推式分类问题,平滑的误差
E
^
\hat{E}
E^可能不是在正确的尺度上。一般来说
∣
∣
E
(
t
+
1
)
∣
∣
2
≤
(
1
−
α
)
∣
∣
E
∣
∣
+
α
∣
∣
S
∣
∣
2
∣
∣
E
(
t
)
∣
∣
2
=
(
1
−
α
)
∣
∣
E
∣
∣
2
+
α
∣
∣
E
(
t
)
∣
∣
2
(4)
||E^{(t+1)}||_2 \le (1-\alpha)||E|| +\alpha||S||_2||E^{(t)}||_2=(1-\alpha)||E||_2+\alpha||E^{(t)}||_2 \tag{4}
∣∣E(t+1)∣∣2≤(1−α)∣∣E∣∣+α∣∣S∣∣2∣∣E(t)∣∣2=(1−α)∣∣E∣∣2+α∣∣E(t)∣∣2(4)
其中
E
(
0
)
=
E
E^{(0)}=E
E(0)=E,我们可以得到
∣
∣
E
(
t
)
∣
∣
2
≤
∣
∣
E
∣
∣
2
||E^{(t)}||_2 \le||E||_2
∣∣E(t)∣∣2≤∣∣E∣∣2。因此,传播不能完全纠正图中所有节点的误差,因为它没有足够的“总质量”,在实验中发现调整残差的规模在实践中有很大的帮助。为此提出了两种缩放残差的方法。
直观地说,我们希望将 E ^ \hat{E} E^ 中的误差大小缩放到与 E E E 中的误差大小近似。我们只知道标记节点上的真实误差,所以我们用训练节点上的平均误差来近似这个尺度。具体来说,令 e j ∈ R c e_j \in \mathbb{R}^c ej∈Rc 与 E E E 中的第 j j j 行相关。之后定义 σ ( 1 ∣ L t ∣ ) ∑ j ∈ L t ∣ ∣ e j ∣ ∣ 1 \sigma(\frac{1}{|L_t|})\sum_{j\in L_t}||e_j||_1 σ(∣Lt∣1)∑j∈Lt∣∣ej∣∣1。那么对于一个未标记节点 i i i 的修正预测是对于 i ∈ U i \in U i∈U Z i , : ( r ) = Z i , : + σ E ^ : , i / ∣ ∣ E ^ : , i T ∣ ∣ 1 Z_{i,:}^{(r)}=Z_{i,:}+\sigma\hat{E}_{:,i}/||\hat{E}_{:,i}^T||_1 Zi,:(r)=Zi,:+σE^:,i/∣∣E^:,iT∣∣1
另外,也可以使用扩散方法,它可以固定训练节点上的已知错误。更具体地说,对 E U ( t + 1 ) = [ D − 1 A E ( t ) ] U E_U^{(t+1)}=[D^{-1}AE^{(t)}]_U EU(t+1)=[D−1AE(t)]U 进行迭代,保持 E L ( t ) = E L E_L^{(t)}=E_L EL(t)=EL 直到 E E E 收敛到 E ^ \hat{E} E^,初始令 E ( 0 ) = E E^{(0)}=E E(0)=E。直观地说,这修正了我们知道的误差值(在标记的节点 L L L 上),而其他节点保持对其邻居的值的平均值直到收敛。使用这种类型的传播, E ( t ) E ^{(t)} E(t) 中条目的最大值和最小值不会超过 E L E_L EL 中条目的最大值和最小值。同时发现学习一个标度超参数 s s s 来产生 Z ( r ) = Z + s E ^ Z^{(r)} = Z + s\hat{E} Z(r)=Z+sE^ 是有效的。
2.3 Smoothing Final Predictions With Prediction Correlation
此时得到了一个分数向量
Z
(
r
)
Z^{(r)}
Z(r),这是通过使用相关误差
e
e
e 的模型对基本预测结果
Z
Z
Z 进行修正而得到的。为了做出最终的预测,我们进一步平滑修正后的预测。其动机是图中的相邻节点很可能具有相似的标签,这是由于网络具有同质性或协调性。因此,我们可以通过另一个标签传播来鼓励平滑的分布。首先,我们从标签的最佳预测
G
∈
R
n
×
c
G\in \mathbb{R}^{n\times c}
G∈Rn×c 开始:
G
L
t
=
Y
L
t
,
G
L
v
,
U
=
Z
L
v
,
U
(
r
)
(5)
G_{L_t}=Y_{L_t},G_{L_v,U}=Z^{(r)}_{L_v,U} \tag{5}
GLt=YLt,GLv,U=ZLv,U(r)(5)
这里,我们将训练节点设置为它们的真实标签,并对验证和未标记的节点使用修正后的预测。基于此我们执行迭代过程
G
(
t
+
1
)
=
(
1
−
α
)
G
+
α
S
G
(
t
)
G^{(t+1)}=(1-\alpha)G + \alpha SG^{(t)}
G(t+1)=(1−α)G+αSG(t),其中
G
(
0
)
=
G
G^{(0)}= G
G(0)=G 直至收敛到最终的预测
Y
^
\hat{Y}
Y^,最后对于每一个节点
i
∈
U
i \in U
i∈U 存在
a
r
g
m
a
x
j
∈
{
1
,
⋯
,
c
}
Y
^
i
j
argmax_{j \in \{1,\cdots,c\}}\hat{Y}_{ij}
argmaxj∈{1,⋯,c}Y^ij。
与误差相关一样,这里的平滑是一个后处理步骤,与其他步骤分离。这种类型的预测平滑在精神上类似于APPNP ,然而,APPNP是端到端训练的,在最终层表示而不是softmax上传播,不使用标签,并且动机不同。
2.4 Summary And Additional Considerations
该方法从一个简单的基本预测 Z Z Z 开始,只使用节点特征而不使用图结构。之后通过传播在训练数据的错误完成对 E ^ \hat{E} E^ 的估计 ,最后得到错误修正的预测 Z ( r ) = Z + E ^ Z^{(r)} = Z + \hat{E} Z(r)=Z+E^ 。最后把这些当作得分向量作用于未标记的节点,并把它们与已知的标签通过另一个LP一步生成最终的平滑预测。此方法称为Correct and Smooth(C&S)。
概括来说,整个模型的算法步骤如下
Z
=
S
i
m
p
l
e
B
a
s
e
F
u
n
c
t
i
o
n
(
X
)
,
Z
∈
R
n
×
c
Z = SimpleBaseFunction(X),Z \in \mathbb{R}^{n \times c}
Z=SimpleBaseFunction(X),Z∈Rn×c
E
L
t
=
Z
L
t
−
Y
L
t
,
E
L
v
=
0
,
E
U
=
0
,
E
∈
R
n
×
c
E_{L_t}=Z_{L_t}-Y_{L_t},E_{L_v}=0,E_U=0,E \in \mathbb{R}^{n \times c}
ELt=ZLt−YLt,ELv=0,EU=0,E∈Rn×c
E
(
t
+
1
)
=
(
1
−
α
)
E
+
α
S
E
(
t
)
E^{(t+1)}=(1-\alpha)E + \alpha SE^{(t)}
E(t+1)=(1−α)E+αSE(t)
E
^
=
a
r
g
m
i
n
t
r
a
c
e
(
W
T
(
I
−
S
)
W
)
+
μ
∣
∣
W
−
E
∣
∣
F
2
,
W
∈
R
n
×
c
\hat{E}=argmintrace(W^T(I-S)W)+\mu||W-E||_F^2,W\in\mathbb{R}^{n\times c}
E^=argmintrace(WT(I−S)W)+μ∣∣W−E∣∣F2,W∈Rn×c
Z
(
r
)
=
Z
+
s
E
^
Z^{(r)} = Z + s\hat{E}
Z(r)=Z+sE^
G
L
t
=
Y
L
t
,
G
L
v
,
U
=
Z
L
v
,
U
(
r
)
G_{L_t}=Y_{L_t},G_{L_v,U}=Z^{(r)}_{L_v,U}
GLt=YLt,GLv,U=ZLv,U(r)
G
(
t
+
1
)
=
(
1
−
α
)
G
+
α
S
G
(
t
)
G^{(t+1)}=(1-\alpha)G + \alpha SG^{(t)}
G(t+1)=(1−α)G+αSG(t)
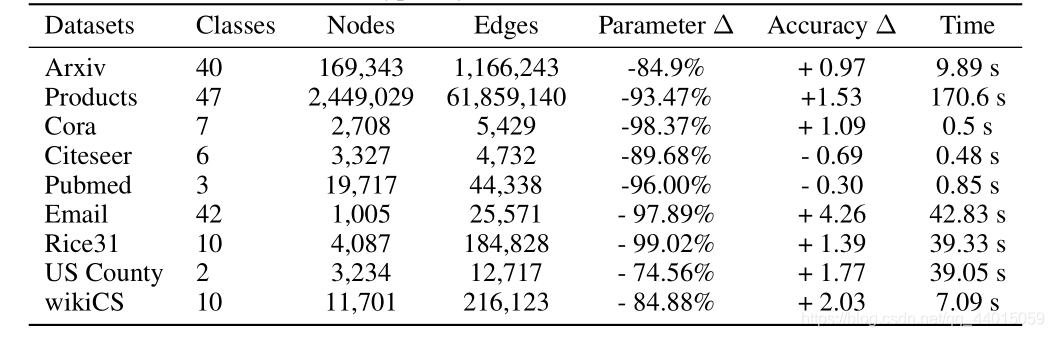
3. Experiments