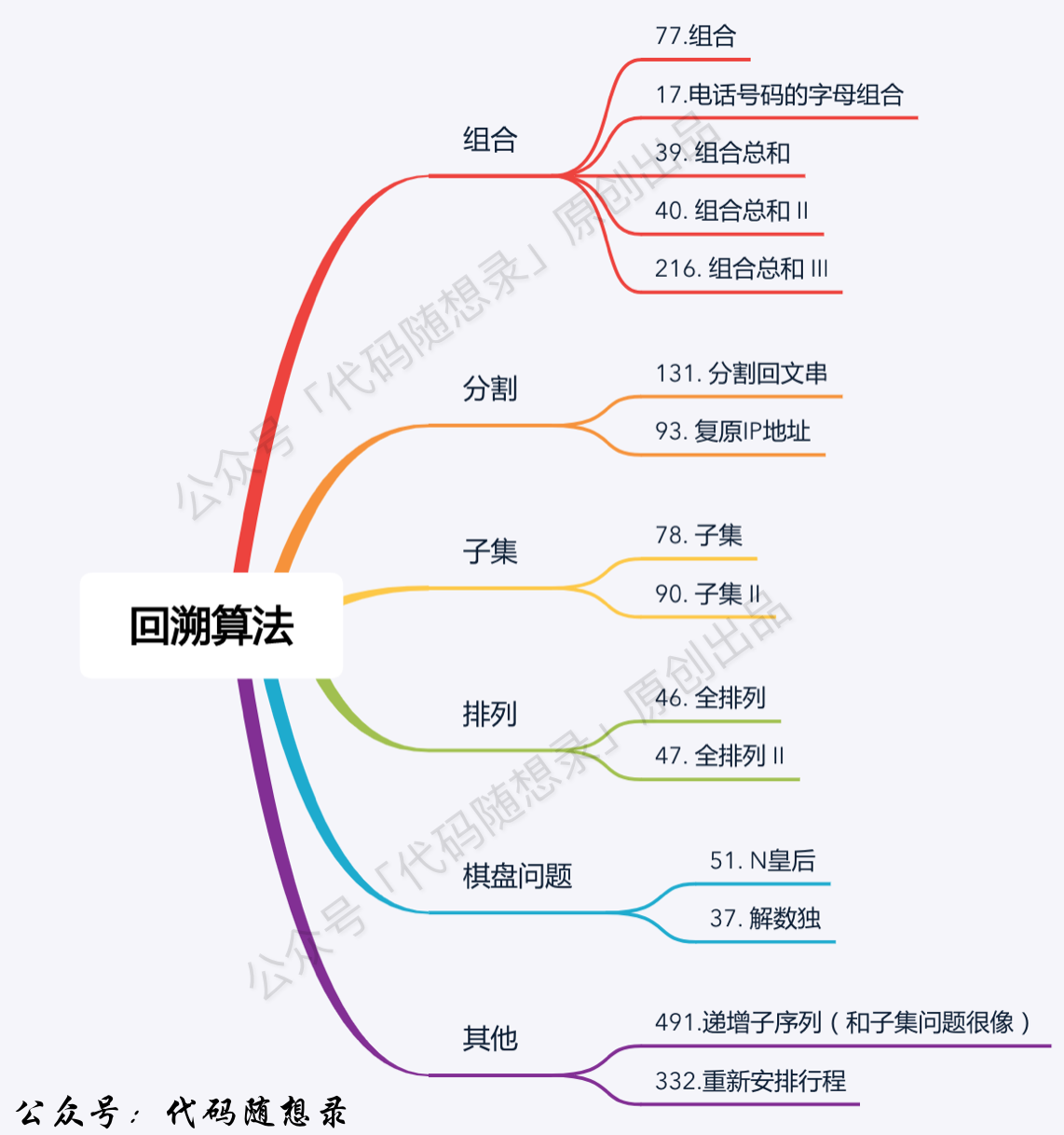
2023-12-22 回溯算法
回溯思想
回溯模版三部曲:
① 回溯函数模版返回值以及参数
② 回溯终止条件
③ 回溯搜索的遍历过程
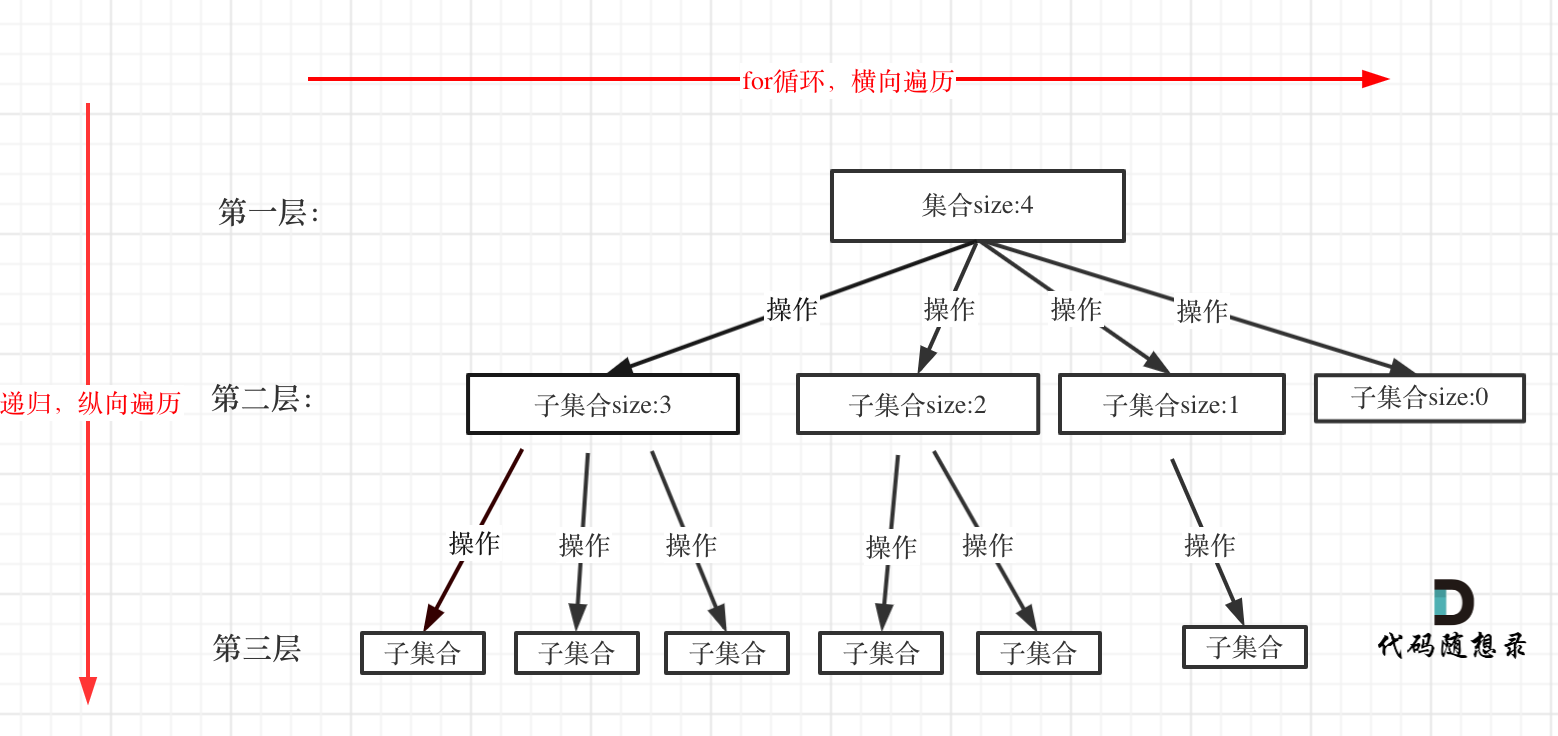
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
这份模板很重要,后面做回溯法的题目都靠它了!
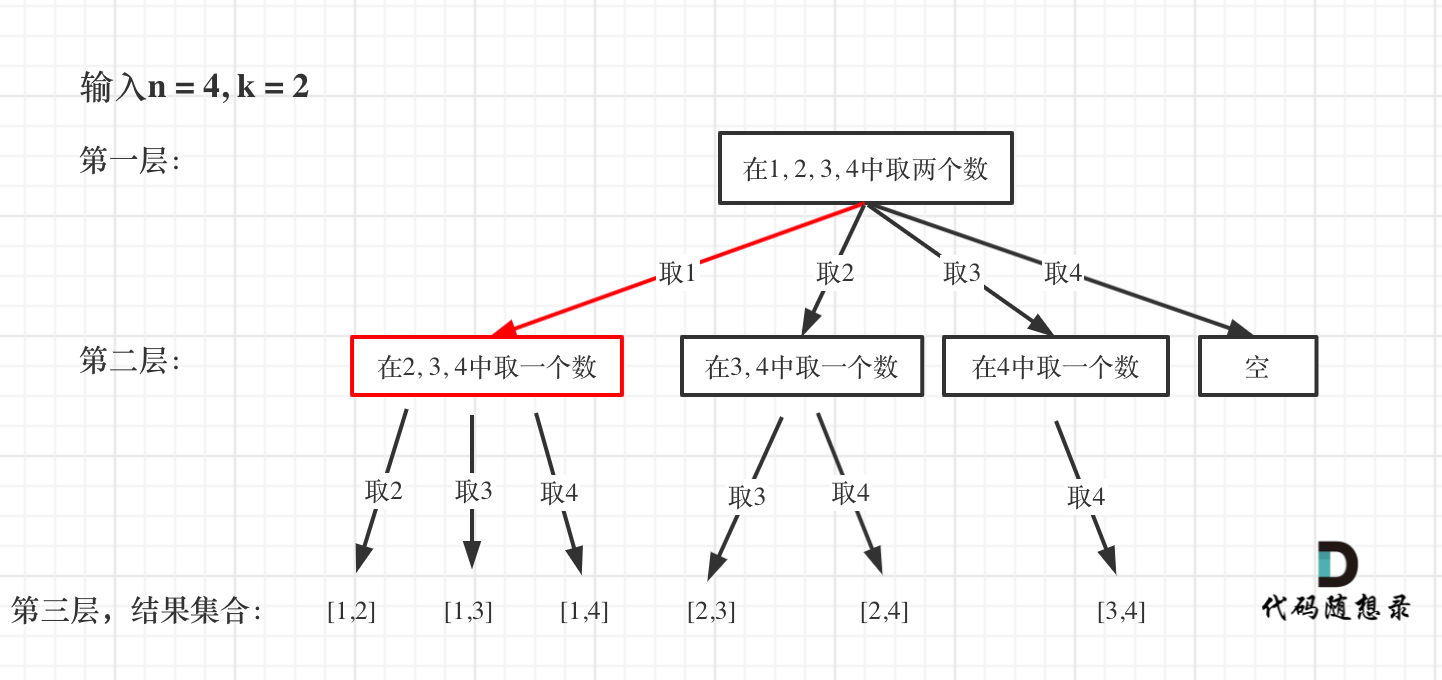
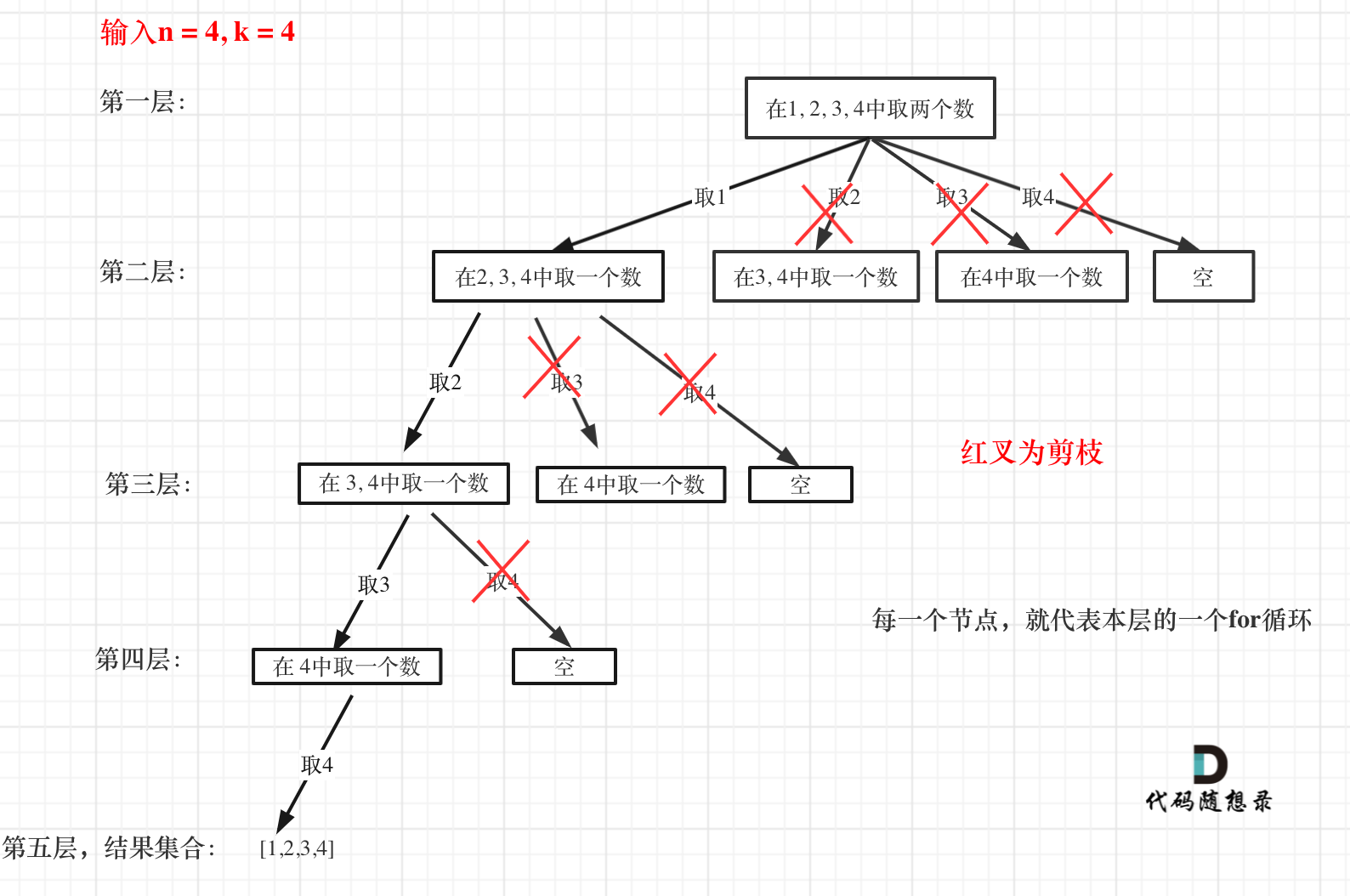
77. 组合
思想:对于这种回溯的问题,其实可以看成一棵树,就是穷举每一种可能的!在此的基础之上然后进行剪枝!
剪枝:可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
self.backtracking(n, k, 1, [], result)
return result
# 回溯的参数以及返回 n k p [] result
def backtracking(self, n, k, startIndex, path, result):
# 回溯终止条件
if len(path) == k:
result.append(path[:])
return
for i in range(startIndex, n + 1):
# 回溯遍历条件
path.append(i)
self.backtracking(n, k, i + 1, path, result)
path.pop() # 回溯,撤销处理节点
优化版本:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = [] # 存放结果集
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, startIndex, path, result):
if len(path) == k:
result.append(path[:])
return
for i in range(startIndex, n - (k - len(path)) + 2): # 优化的地方
path.append(i) # 处理节点
self.backtracking(n, k, i + 1, path, result)
path.pop() # 回溯,撤销处理的节点