最优控制 1：最优控制中不同情形下泛函取到极值的必要条件

最优控制 (1)：最优控制中不同情形下泛函取到极值的必要条件

引言

众所周知，强化学习在控制领域有一个别称，叫自适应动态规划 (Adaptive Dynamic Programming )或近似动态规划 (Approximate Dynamic Programming)。这个东西最开始的初衷 (不论是被刻意赋予的初衷，还是的的确确有这么一个初衷)是去解决最优控制的问题。

最优控制其实与泛函的联系十分紧密。如果说函数本身的求解比较复杂的话，只能说泛函的求解更复杂。很多函数本身是具备一些形式和性质的，只不过是求解过程太复杂。但是泛函本身就是一个“虚无缥缈”的东西，甚至连函数的形式都不知道，只知道零点的函数值为零，这让求解根本无从下手。

遗憾的是，很多最优控制问题就偏偏要求解这些泛函问题。目前已经有很多工具可以做到，极小值原理，动态规划，黎卡提方程工具包之类的 (我都没用过，只是听说过)，但是有时候他的求解速度真的是感人。

所以，强化学习后来就被用来解最优控制中的泛函，举个例子：

已知系统模型 $\dot{x}=f(x)$，某一时刻的正定代价函数为 $g=g(x,\dot{x},t)$，求解一个控制器 $u(t)$，使得
$$J={\int }_{t_0}^{t_1}{k}_{1}g(x,\dot{x},t)+k_2{u}^{2}dt$$最小。

如果 $f$ 和 $g$ 都比较简单，其实用笔也能算出来。但是如果 $f$ 和 $g$ 都比较复杂，并且没有任何规律可循，那么不仅用笔没法算，而且用工具包也不好求解，这个时候强化学习就体现出作用了(虽然不一定好使)。

因此要了解强化学习控制，掌握必须的最优控制的基本理论和尝试也是必要的。

一般问题

将上式一般化，可以得到一般化的泛函形式的代价函数为
$$J(x)={\int }_{t_0}^{t_1}g\left[x(t),\dot{x}(t),t\right]dt$$
简记为
$$J(x)={\int }_{t_0}^{t_1}g(x,\dot{x})dt$$
最优控制的目标，就是解出 $x(t)$，即当 $x$ 的时域曲线应该是什么样的时候， $J(x)$ 最小。下边分多钟情况讨论。

1. $t_0$ 固定，$t_1$ 固定，$x_0=x(t_0)$ 固定，$x_1=x(t_1)$ 固定

由于初始时间、终止之间、初始状态和终止状态都被固定，所以 $J$ 的不确定性只能被中间时刻的 $x$ 影响，那么记 $x$ 的变分为 $\delta x$，进而所导致的 $J$ 的变分为 $\delta J$。则有
$$\begin{array}{r}\begin{array}{rl}\delta J& =J(x+\delta x,\dot{x}+\delta \dot{x})-J(x)\\ & ={\int }_{t_0}^{t_1}g(x+\delta x,\dot{x}+\delta \dot{x})-g(x,\dot{x})dt\end{array}\end{array}$$
对 (1) 中第一项在 $(x,\dot{x})$ 处一次 Taylor 展开
$$g(x+\delta x,\dot{x}+\delta \dot{x})=g(x,\dot{x})+\frac{\partial g(x,\dot{x})}{\partial x}\delta x+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}$$
代回 (1)，有
$$\begin{array}{r}\begin{array}{rl}\delta J& ={\int }_{t_0}^{t_1}g(x+\delta x,\dot{x}+\delta \dot{x})-g(x,\dot{x})dt\\ & ={\int }_{t_0}^{t_1}g(x,\dot{x})+\frac{\partial g(x,\dot{x})}{\partial x}\delta x+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}-g(x,\dot{x})dt\\ & ={\int }_{t_0}^{t_1}\frac{\partial g(x,\dot{x})}{\partial x}\delta x+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}dt\end{array}\end{array}$$
对 (2) 中第二项分部积分，有
$${\int }_{t_0}^{t_1}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}dt={\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta x|}_{t_0}^{t_1}-{\int }_{t_0}^{t_1}\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta xdt$$
代回 (2)，有
$$\begin{array}{r}\begin{array}{rl}\delta J& ={\int }_{t_0}^{t_1}\frac{\partial g(x,\dot{x})}{\partial x}\delta x+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}dt\\ & ={\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta x|}_{t_0}^{t_1}+{\int }_{t_0}^{t_1}\frac{\partial g(x,\dot{x})}{\partial x}\delta x-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta xdt\end{array}\end{array}$$
由于 $x(t_0)$ 和 $x(t_1)$ 都固定，所以 $\delta x(t_0)=\delta x(t_1)=0$，进而有
$$\begin{array}{r}\begin{array}{rl}\delta J& ={\int }_{t_0}^{t_1}\left[\frac{\partial g(x,\dot{x})}{\partial x}-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\right]\delta xdt\end{array}\end{array}$$对于任意 $x$ 均成立，所以，很自然地，有
$$\begin{array}{r}\begin{array}{r}\frac{\partial g(x,\dot{x})}{\partial x}-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}=0\end{array}\end{array}$$
这就是大名鼎鼎的欧拉方程，也叫欧拉-拉格朗日方程(这个结论得出是有定理保证的)。这个结论可以被用来解释为什么两点之间线段最短。

2. $t_0$ 固定，$x_0=x(t_0)$ 固定，$t_1$ 自由，$x_1=x(t_1)$ 自由

这种情况下由于末端时刻和末端状态都是可变的，因此 $J$ 的变分是由 $\delta t_1$ 和 $\delta x$共同导致的。这里用一个图去表示

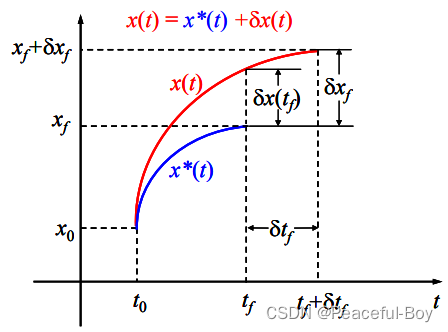
这里，蓝色的曲线表示最优的曲线，红色的曲线表示经过变分变化之后的曲线。与上一种情况类似，代价函数的变分为
$$\begin{array}{r}\begin{array}{rl}\delta J& =J(x+\delta x,\dot{x}+\delta \dot{x},t+\delta t)-J(x)\\ & ={\int }_{t_0}^{t_1+\delta t_1}g(x+\delta x,\dot{x}+\delta \dot{x})dt-{\int }_{t_0}^{t_1}g(x,\dot{x})dt\\ & ={\int }_{t_0}^{t_1}g(x+\delta x,\dot{x}+\delta \dot{x})-g(x,\dot{x})dt+{\int }_{t_1}^{t_1+\delta t_1}g(x+\delta x,\dot{x}+\delta \dot{x})dt\end{array}\end{array}$$
同样地，把 $g(x+\delta x,\dot{x}+\delta \dot{x})$ 在 $(x,\dot{x})$ 处 Taylor 展开，代回 (6)，(6) 中第一项有
$$\begin{array}{r}\begin{array}{rl}\delta J_1& ={\int }_{t_0}^{t_1}g(x+\delta x,\dot{x}+\delta \dot{x})-g(x,\dot{x})dt\\ & ={\int }_{t_0}^{t_1}\frac{\partial g(x,\dot{x})}{\partial x}\delta x+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}dt\end{array}\end{array}$$
对 (6) 中第二项应用中值定理，有
$$\begin{array}{r}\begin{array}{rl}\delta J_2& ={\int }_{t_1}^{t_1+\delta t_1}g(x+\delta x,\dot{x}+\delta \dot{x})dt\\ & =g\left[x(t_1+\theta \delta t_1),\dot{x}(t_1+\theta \delta t_1,),t_1+\theta \delta t_1\right]\delta t_1\end{array}\end{array}$$
其中 $0<\theta <1$。考虑到标量函数 $g$ 是连续函数，所以当 $t_1$ 的变分 $\delta t_1\to 1$ 时，$g$ 的变化量是趋近于 0 的。即
$$g\left[x(t_1+\theta \delta t_1),\dot{x}(t_1+\theta \delta t_1,),t_1+\theta \delta t_1\right]\delta t_1=g\left[x(t_1),\dot{x}(t_1)\right]+ϵ$$
所以有
$$\begin{array}{r}\begin{array}{rl}\delta J_2& =g\left[x(t_1),\dot{x}(t_1)\right]\delta t_1=g(x,\dot{x})\delta t_1\end{array}\end{array}$$
将 $\delta J_1$ 和 $\delta J_2$ 代回 (6)，有
$$\begin{array}{r}\begin{array}{rl}\delta J& =g(x,\dot{x})\delta t_1+{\int }_{t_0}^{t_1}\frac{\partial g(x,\dot{x})}{\partial x}\delta x+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta \dot{x}dt\end{array}\end{array}$$
同理，对上式积分第二项应用分部积分，得到：
$$\begin{array}{r}\begin{array}{rl}\delta J& =g(x,\dot{x})\delta t_1+{\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta x|}_{t_0}^{t_1}\\ & +{\int }_{t_0}^{t_1}\left[\frac{\partial g(x,\dot{x})}{\partial x}-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\right]\delta x\cdot dt\\ & =g(x,\dot{x})\delta t_1+\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta x(t_1)+{\int }_{t_0}^{t_1}\left[\frac{\partial g(x,\dot{x})}{\partial x}-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\right]\delta x\cdot dt\end{array}\end{array}$$
这个时候就用到上面的图了，通过上面的图可以发现，$\delta t_1$ 与 $\delta x(t_1)$ 是有关系的，这个关系是
$$\delta x(t_1)=\delta x_1-\dot{x}\cdot \delta t_1$$
代入 (11)，进而有
$$\begin{array}{r}\begin{array}{rl}\delta J& ={\int }_{t_0}^{t_1}\left[\frac{\partial g(x,\dot{x})}{\partial x}-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\right]\delta x\cdot dt\\ & +\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta x_1\\ & +\left[g(x,\dot{x})-\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\dot{x}\right]\delta t_1\end{array}\end{array}$$
当最优时， $\delta J$恒为零，这就很有意思了，那就说明不管怎么样，里面每一项必须都得是零才行。因此，同样地，有欧拉方程存在
$$\frac{\partial g(x,\dot{x})}{\partial x}-\frac{d}{dt}\frac{\partial g(x,\dot{x})}{\partial \dot{x}}=0$$
此外，还必须满足额外的条件
$$\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\delta x_1+\left[g(x,\dot{x})-\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\dot{x}\right]\delta t_1=0$$成立，这个条件被称为横截条件。

这里可以分两种情况讨论，当 $x_1$ 不受 $t_1$ 约束时，那么上式两部分就必须分别为零：
$${\frac{\partial g(x,\dot{x})}{\partial \dot{x}}|}_{x=x_1}=0,g(x_1,{\dot{x}}_1)=0$$

若 曲线的末端 $x_1$ 是受另外一条曲线 $x_1=\gamma (t_1)={\gamma }_1$ 约束时，再参考第二张图

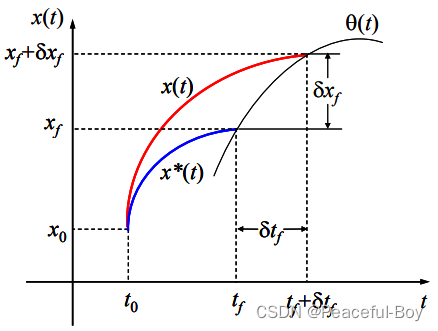
可以看出，$\delta x_1=\dot{\theta }(t_1)\delta t_1$ (近似成立)。进而有横截条件：
$$g(x_1,{\dot{x}}_1)+{\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\left(\dot{\theta }-\dot{x}\right)|}_{t=t_1}=0$$成立。

3. $t_0$ 固定，$x_0=x(t_0)$ 固定，$t_1$ 固定，$x_1=x(t_1)$ 自由

与第二种情况类似，欧拉方程还是要成立的，除此之外，由于 $t_1$ 已经被固定，所以一切有$\delta t_1$产生的变化都消失了，而且只能是 $x_1$ 自由。所以，式 (12)的第三行就消失了，那么横截条件就简化为
$${\frac{\partial g(x,\dot{x})}{\partial \dot{x}}|}_{x=x_1}=0$$

4. $t_0$ 固定，$x_0=x(t_0)$ 固定，$x_1=x(t_1)$ 固定，$t_1$ 自由

与第二种情况类似，欧拉方程还是要成立的，除此之外，由于 $x_1$ 已经被固定，所以一切有$\delta x_1$产生的变化都消失了，而且只能是 $t_1$ 自由。所以，式 (12)的第二行就消失了，那么横截条件就简化为
$${g(x,\dot{x})-\frac{\partial g(x,\dot{x})}{\partial \dot{x}}\dot{x}|}_{x=x_1}=0$$

总结

直接贴图吧，表格太大了。

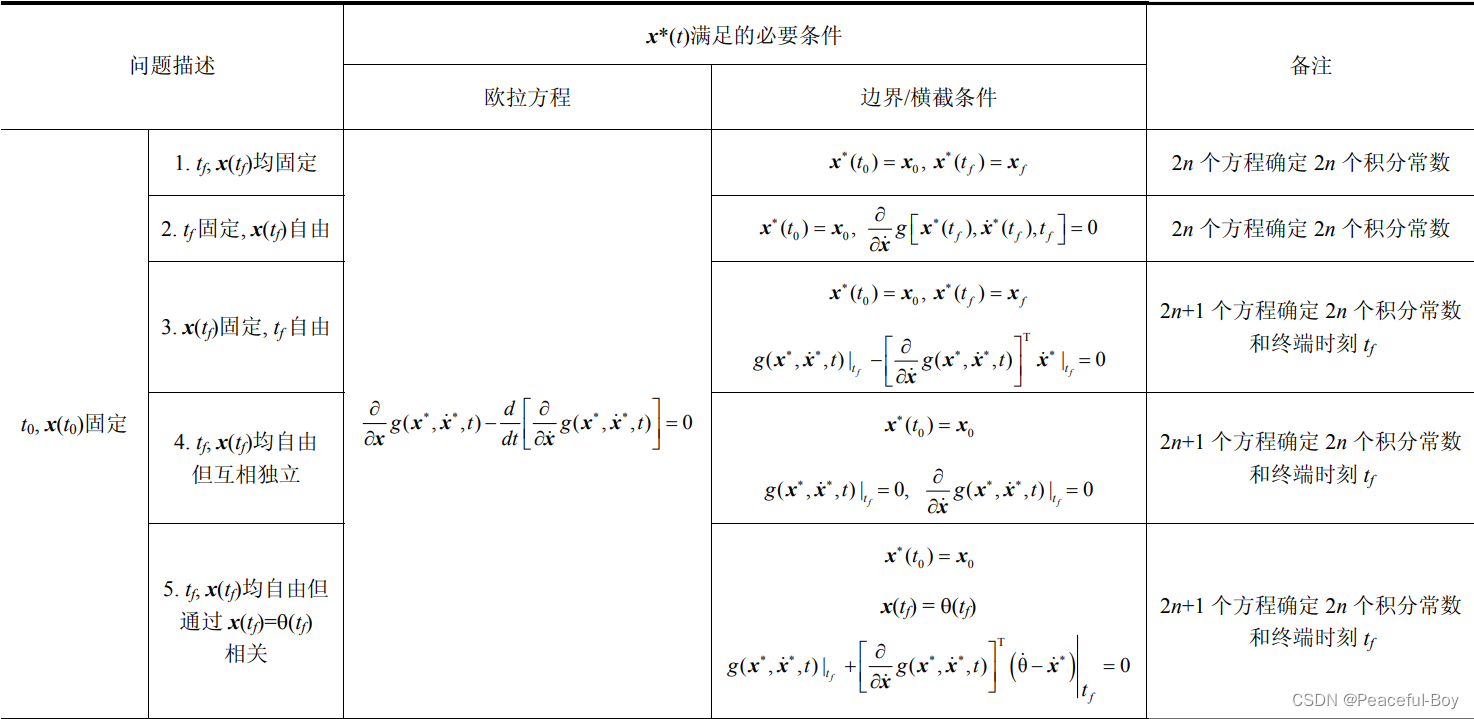
学习了这个工具之后，很多常见的小数学问题都有一个新视角去计算。比如两点之间为什么线段最短；找到某一定点到曲线方程的最短距离，等等。