PSM和HTE的异同：以感冒场景为例

笔者在刚开始接触PSM和HTE时，对这两个方法算出来的结果十分困惑：既然这两个方法都是计算实验处理效应，那么选择PSM还是HTE又有什么不同呢？随着笔者对这两个方法的深入研究，发现这两个方法的本质不同在于：

PSM的计算结果是ATT，HTE的计算结果是CATE；

要理解这个差异，首先要理解什么是ATT和CATE。我们以平时常见的感冒场景为例：当我们感冒时，我们可以选择吃感冒药；也可以不吃感冒药，多喝热水自己抗过去。这里我们想探究的是吃感冒药对健康有多大影响，那么我们定义T1代表吃感冒药，T0代表不吃感冒药，Y为健康评分。协变量X可能有很多，比如年龄、性别、近1年就医次数等等。

缩写英文中文数学表达例子估计方法
ATEAverage Treatment Effect平均处理效应E[Y1-Y0]感冒药对所有人群的效果

ATT

Average Treatment Effect on the Treated受处理人群（实验组）平均处理效果E[Y1-Y0|T=1]感冒药对所有吃感冒药人群的效果PSM
CATEConditional Average Treatment Effect条件平均处理效应E[Y1-Y0|X=x]感冒药对所有吃感冒药的年老、男性人群的效果HTE

那么，以上统计量之间应如何相互转化呢？

为了简化问题，我们假设协变量X只有年龄（年轻、年老）和性别（男、女），所以人群可以划分为以下四组，四组人群HTE的估计结果如下：

组别年龄性别CATE总样本中Gn的占比吃感冒药（T=1）样本中Gn的占比
G1年轻男性CATE125%15%
G2年轻女性CATE225%30%
G3年老男性CATE325%20%
G4年老女性CATE425%35%

那么，对于ATE和ATT我们有：

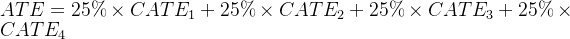
ATE=25\%\times CATE_{1}+25\%\times CATE_{2}+25\%\times CATE_{3}+25\%\times CATE_{4}

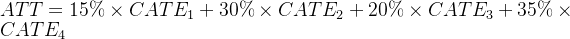
ATT=15\%\times CATE_{1}+30\%\times CATE_{2}+20\%\times CATE_{3}+35\%\times CATE_{4}

我们该怎么理解上面的公式呢：

如果我们知道某特定X群体在总样本中占比，我们可以利用CATE加权计算得到ATE；

如果我们知道某特定X群体在实验组（T=1）中的占比，我们可以利用CATE加权计算得到ATT。