【论文阅读】(2019)Enhanced Pseudo-polynomial Formulations for Bin Packing and Cutting Stock Problems
文章目录
论文来源:(2019)Enhanced Pseudo-polynomial Formulations for Bin Packing and Cutting Stock Problems
作者:Maxence Delorme 等人
一、摘要
- 我们研究经典装箱和下料问题的伪多项式公式。
- 我们首先从文献中提出了主要的基于模式和伪多项式公式之间的优势和等价关系的概述。
- 然后我们引入reflect,这是一个新的公式,它只使用一半的bin容量来建模一个实例,并且比经典模型需要更少的约束和变量。
- 当面元容量过高时,我们提出了利用列生成和对偶信息来补偿反射弱点的上限和下限技术。
- 我们还提出了解决两个有趣的问题变体的技术的非平凡的修改,即可变大小的装箱问题和带有物品碎片的装箱问题。
- 在基准实例上的大量计算测试表明,我们的算法在所有问题上都达到了最先进的结果,改进了以前的算法,并找到了几个新的经证明的最优解。
二、介绍
在本文中,我们继续伪多项式模型的研究,提出了理论和计算的兴趣结果。我们首先关注存在于众所周知的基于模式和伪多项式公式之间的关系,第一次提供了它们之间等价和支配的完整图像。然后,我们提出了一个新的有效的公式,称为反射,它只需要一半的bin容量来建模一个CSP实例。
与所有伪多项式公式一样,reflect在解决容量非常大的实例时也有困难。因此,我们用几种技术对其进行了改进,从而产生了一种叫做reflect+的算法,它具有出色的计算性能。具体而言,我们提供了以下贡献。
- 我们证明了CSP的一次切割和弧流公式是等价的(即,它们具有相同的连续松弛值)。
- 我们扩展了以前的结果,并提供了一个存在于主要的基于模式和伪多项式MILP公式之间的优势和等价关系的清晰图像,这些公式已被提出用于BPP和CSP。
- 我们介绍了我们的新公式,反映,并表明,它改善了经典弧流需要明显更少的约束和变量。
- 我们开发了基于反射与列生成、双重切割和启发式的结合使用的改进技术。我们表明,我们的启发式算法比传统的方法更快和更有效的解决方案的集合覆盖模型与限制集合的列。
- 我们通过设计公式和算法来解决两个重要的BPP变量,即可变大小的BPP和带有项目碎片的BPP,从而扩展了reflect和reflect+。
- 我们进行了大量的计算测试,并表明我们的算法达到了最先进的结果,改进了文献中以前的算法,为BPP和CSP找到了几个新的最优解,并最优地解决了可变大小的BPP和带有项目碎片的BPP的所有尝试实例。
三、BPP和CSP的著名MILP公式
在本节中,我们正式描述了BPP和CSP,给出了必要的符号,并介绍了文献中为其解决方案开发的主要公式。
3.1 问题描述和符号
在BPP中,给定一组n个项目,每个项目的权重为 w j ( j = 1 , . . . , n ) w_j (j = 1,...,n) wj(j=1,...,n) 以及容量为 c c c 的无限个相同箱子。目标是将所有物品装入最少数量的箱柜中,使得任何箱柜中物品重量的总和不超过容量。
为了更好地适应包装或切割的概念,在下文中,当提到 w j w_j wj时,我们交替使用重量和宽度这两个术语。
我们假设所有的输入值都是整数,并且 0 < w j < c 0 < w_j < c 0<wj<c 对任何 j j j 都成立。
CSP具有与BPP相同的目标,但是其输入包括一组m个项目类型。每个项目类型 j j j 具有对 d j d_j dj 个项目的需求,所有项目都具有宽度 w j ( j = 1 , . . . , m ) w_j (j = 1,...,m) wj(j=1,...,m)
通过将具有相同宽度的所有项目分组为项目类型,可以从BPP中获得CSP实例。
因此,CSP的求解方法也能求解BPP,反之亦然。
除非另有说明,我们下面报道的公式指的是CSP。
我们用 F X F_X FX 来表示一般的MILP公式。
我们使用 L ( F X ) L(F_X) L(FX)来表示 F X F_X FX 的连续(线性规划)松弛,这是通过从 F X F_X FX 中去除整数约束而获得的。
当不产生混淆时,我们也用 L ( F X ) L(F_X) L(FX) 来表示 L ( F X ) L(F_X) L(FX) 的最优解值。
我们说公式 F X F_X FX 等价于公式 F Y F_Y FY ,如果 L ( F X ) = L ( F Y ) L(F_X) = L(F_Y) L(FX)=L(FY) 在任何情况下成立。
当我们处理极小化问题时,我们说公式 F X F_X FX 支配公式 F Y F_Y FY ,如果 L ( F X ) ≥ L ( F Y ) L(F_X) ≥ L(F_Y) L(FX)≥L(FY) 对任何实例成立,并且 L ( F X ) > L ( F Y ) L(F_X) > L(F_Y) L(FX)>L(FY) 对至少一个实例成立。
如果 F X F_X FX 支配 F Y F_Y FY ,那么我们也说 F X F_X FX 包含于 F Y F_Y FY 。假设一个给定的公式包含一个变量 x x x ,我们用符号 x x x 来表示 x x x 在该公式的给定解中所取的值。
3.2 基于方案(Pattern)的公式
我们将方案 p p p 定义为数组 ( a 1 p , . . . , a m p ) (a_{1p},...,a_{mp}) (a1p,...,amp) ,其中 a j p a_{jp} ajp 是一个非负整数,给出方案中包含的 j j j 类型的项目数。
Gilmore和Gomory (1961)将每个方案 p p p 与一个整数决策变量 ξ p ξ_p ξp 相关联,表示方案被选择的次数,并将CSP建模为以下集合覆盖问题:
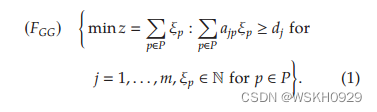
注意,在(1)中,没有什么能阻止 a j p a_{jp} ajp 大于 d j d_j dj ,因此,可能存在 F G G F_{GG} FGG或其连续松弛 L ( F G G ) L(F_GG) L(FGG) 的最优解,其中包括包含大量超出需求的项目的方案。
3.3 伪多项式公式
伪多项式公式涉及大量的变量和约束,因此,它们通常与适当的简化技术一起在文献中提出。我们在这一节集中讨论不使用任何约简的基本模型,并在第4节的末尾讨论现有的约简技术。
one-cut 公式( F O C F_{OC} FOC )是由Rao (1976)和Dyckhoff (1981)正式提出的。它通过选择一组切割来模拟物理切割过程,每个切割将箱子(或箱子的一部分)分成两个更小的部分:左边的和右边的。左边的部分是一个项目,右边的部分是一个项目或剩余部分,可以通过连续切割重新用于生产更小的项目。
为了描述这个模型,我们需要一些额外的符号。设 W = { w 1 , w 2 , . . . } W = \{w_1,w_2,...\} W={w1,w2,...} 定义不同项目宽度的集合, S \mathscr{S} S 是不超过 c c c 的项目宽度组合的集合。集合 S \mathscr{S} S 可以通过标准DP计算,并正式表述为
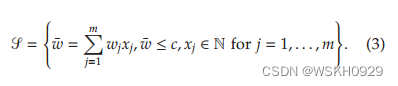
设 R \mathscr{R} R 定义剩余宽度集,计算方法为 R = { c − w ˉ : w ˉ ∈ S 和 w ˉ ≤ c − m i n j { w j } } \mathscr{R}=\{c-\bar{w}:\bar{w}\in\mathscr{S}和\bar{w}\le c-min_j\{w_j\}\} R={c−wˉ:wˉ∈S和wˉ≤c−minj{wj}} 。
由切割产生的任何左块的宽度在 W W W 中,而任何右块(包括 c c c )的宽度在 R \mathscr{R} R 中。
对于任意一个给定的宽度 q ∈ W ∪ R q\in W \cup \mathscr{R} q∈W∪R,当存在 j j j 满足 w j = q w_j=q wj=q 时,令 L q = d j L_q=d_j Lq=dj,否则令 L q = 0 L_q=0 Lq=0。
one-cut 使用三组额外的宽度:
集合 A ( q ) A(q) A(q) 包含可用于产生宽度为 q q q 的左片的片宽度(如果有的话): A ( q ) = { p ∈ R : p > q } f o r q ∈ W A(q)=\{p\in \mathscr{R}:p>q\} \ for\ q\in W A(q)={p∈R:p>q} for q∈W 和 A ( q ) = ∅ f o r q ∉ W A(q)=\empty \ for\ q\notin W A(q)=∅ for q∈/W
集合 B ( q ) = { p ∈ W : p + q ∈ R } B(q) = \{p ∈ W : p + q ∈ \mathscr{R}\} B(q)={p∈W:p+q∈R} 包含这样的项目宽度,不管是否作为左块切割,对于 q ∈ R q ∈ \mathscr{R} q∈R都会产生宽度为 q q q 的右块。
集合 C ( q ) = { p ∈ W : p < q } C(q)=\{p\in W:p<q\} C(q)={p∈W:p<q} 包含可以通过使用 q ∈ R q ∈ \mathscr{R} q∈R的宽度 q q q 的余数作为左片切割的项目宽度。
one-cut 使用整数决策变量 y p q y_{pq} ypq,给出切割成宽度为 q q q 的左片的宽度为 p p p 的片的数量。然后,模型为
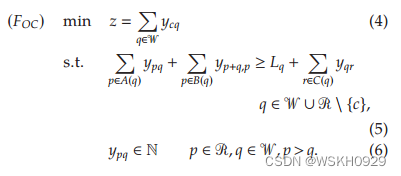
虽然函数(4)最小化了所使用的箱的数量,但是约束(5)确保了具有宽度 q q q 的左和右块的总和不小于宽度 q q q 的需求加上宽度 q q q 的剩余被重新切割以产生其他项目的次数。
弧流公式( F A F ) F_{AF}) FAF) 是Valério de Carvalho (1999)为CSP正式提出的,并建立在Shapiro (1968)和Wolsey (1977)的网络基础上。
令
G
=
(
V
,
A
)
\mathscr{G}=(\mathscr{V},\mathscr{A})
G=(V,A) 是一个图,它的顶点集
V
=
{
0
,
1
,
.
.
.
,
c
−
1
,
c
}
\mathscr{V}=\{0,1,...,c-1,c\}
V={0,1,...,c−1,c},弧集合
A
=
A
I
∪
A
l
\mathscr{A}=\mathscr{A}_I \cup \mathscr{A}_{\mathscr{l}}
A=AI∪Al
其中
A
I
=
{
(
d
,
e
)
:
d
,
e
∈
S
a
n
d
存在
j
∈
{
1
,
.
.
.
,
m
}
:
e
−
d
=
w
j
}
\mathscr{A}_I=\{(d,e):d,e\in \mathscr{S}\ and \ 存在j\in \{ 1,...,m\}:e-d=w_j\}
AI={(d,e):d,e∈S and 存在j∈{1,...,m}:e−d=wj}是项目弧的集合
A
l
=
{
(
d
,
d
+
1
)
:
d
=
0
,
1
,
.
.
.
,
c
−
1
}
\mathscr{A}_l=\{(d,d+1):d=0,1,...,c-1\}
Al={(d,d+1):d=0,1,...,c−1}是损失弧的集合
物品弧模拟物品在箱中的位置,通过(3)实现,而损失弧模拟空箱部分。
容器的填充对应于从根节点 0 0 0 开始,并从节点 c c c 结束的路径
设 δ + ( e ) ( δ − ( e ) ) δ^+(e)(δ^-(e)) δ+(e)(δ−(e))给出从顶点 e e e 发出(进入)的弧的子集,通过引入整数变量 x d e x_{de} xde,表示弧 ( d , e ) (d,e) (d,e) 被选择的次数,CSP变成
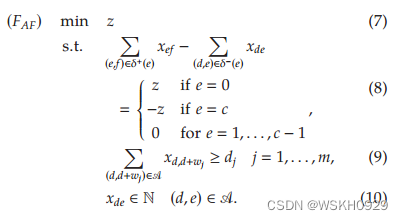
目标函数(7)最小化由变量
z
z
z 表示的箱的数量,而约束条件(8)施加流量守恒,约束条件(9)确保满足需求。
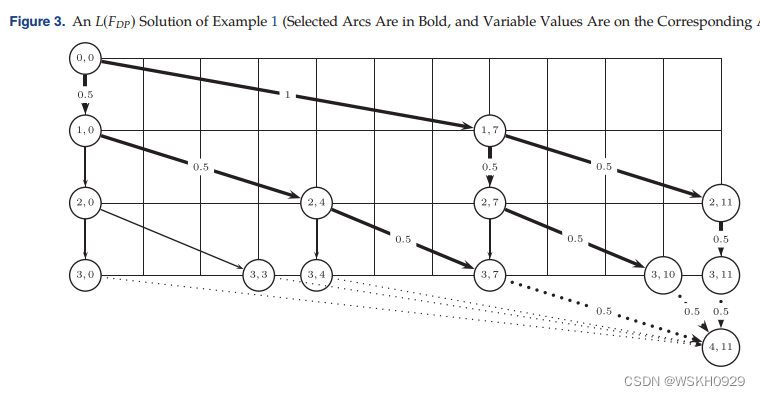
动态规划流公式( F D P F_{DP} FDP)由Cambazard和O’Sullivan (2010)正式引入BPP,但与 F A F F_{AF} FAF类似,它源于Shapiro (1968)和Wolsey (1977)的早期工作。
它可以被视为 F A F F_{AF} FAF 的分解形式,使用从DP表获得的扩展图。
详细的说,令
G
′
=
(
V
′
,
A
′
)
\mathscr{G}'=(\mathscr{V}',\mathscr{A}')
G′=(V′,A′) 为一个DP图
其中
V
′
=
{
(
j
,
d
)
:
j
=
0
,
.
.
.
,
n
;
d
=
0
,
.
.
.
,
c
}
∪
{
(
n
+
1
,
c
)
}
\mathscr{V}'=\{(j,d):j=0,...,n;d=0,...,c\} \cup \{(n+1,c)\}
V′={(j,d):j=0,...,n;d=0,...,c}∪{(n+1,c)},每个DP状态都有一个顶点,外加一个虚拟节点
(
n
+
1
,
c
)
(n+1,c)
(n+1,c)
A
′
=
{
(
(
j
,
d
)
,
(
j
+
1
,
e
)
)
:
(
j
,
d
)
∈
V
′
;
(
j
+
1
,
e
)
∈
V
′
}
\mathscr{A}'=\{((j,d),(j+1,e)):(j,d)\in \mathscr{V}';(j+1,e)\in \mathscr{V}'\}
A′={((j,d),(j+1,e)):(j,d)∈V′;(j+1,e)∈V′} 包含连接两个连续DP状态的弧线。
有两种类型的弧线:一种是 e = d + w j e = d + w_j e=d+wj 在箱子被 d d d 个单位部分填满时对项目 j j j 的选择进行建模,另一种是 e = d e = d e=d 丢弃 d d d 中 j j j 的选择
具有 j = n j = n j=n 的所有顶点 ( j , d ) (j,d) (j,d) 都连接到虚拟顶点 ( n + 1 , c ) (n + 1,c) (n+1,c) 。
从 ( 0 , 0 ) (0,0) (0,0) 到 ( n + 1 , c ) (n + 1,c) (n+1,c) 的路径表示可行的面元填充
决策变量 φ j , d , j + 1 , e \varphi_{j,d,j+1,e} φj,d,j+1,e 与每个弧相关联 ( ( j , d ) , ( j + 1 , e ) ) ∈ A ′ ((j,d),(j+1,e)) \in \mathscr{A}' ((j,d),(j+1,e))∈A′
通过设置
V
0
′
=
V
′
\
{
(
0
,
0
)
,
(
n
+
1
,
c
)
}
\mathscr{V}_0'=\mathscr{V}' \backslash \{(0,0),(n+1,c)\}
V0′=V′\{(0,0),(n+1,c)},BPP可以被建模为:

约束(12)强制流量守恒,约束(13)强制采用BPP符号的每个项目被选择一次。变量被设置为由(14)取整数值,但是由于(13),与弧
(
(
j
−
1
,
d
)
,
(
j
,
d
+
w
j
)
)
((j-1,d),(j,d + w_j))
((j−1,d),(j,d+wj)) 相关的变量是二进制的。
CSP实例可以由 F D P F_{DP} FDP 通过将每个项目类型 j j j 分成 d j d_j dj 个项目来建模,从而获得具有 n = ∑ i = 1 m d j n=\sum^m_{i=1}{d_j} n=∑i=1mdj 个项目的BPP实例。
四、模型之间的关系
在这一节中,我们证明了基于模式的公式和伪多项式公式之间的关系。据我们所知,这是第一次提供该研究领域的完整描述。我们首先需要两个初步结果。
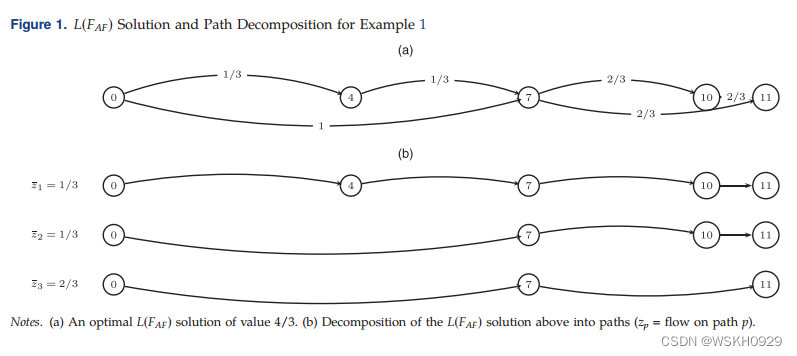
引理1(Valério de Carvalho 1999):arcflow或其连续松弛的任何解都可以分解成一组路径
引理1基于将非负流分解成路径和圈(参见Ahuja等人1993年的第3章),唯一的注释是弧流图是非循环的,只有路径可能出现。
如图1(a)所示,最佳
L
(
F
A
F
)
L(F_{AF})
L(FAF) 解的值为
4
/
3
4/3
4/3 ,由
x
0
,
7
=
1
、
x
0
,
4
=
1
/
3
、
x
4
,
7
=
1
/
3
、
x
7
,
10
=
2
/
3
、
x
7
,
11
=
2
/
3
x_{0,7} = 1、x_{0,4} = 1/3、x_{4,7} = 1/3、x_{7,10} = 2/3、x_{7,11} = 2/3
x0,7=1、x0,4=1/3、x4,7=1/3、x7,10=2/3、x7,11=2/3 和
x
10
,
11
=
2
/
3
x_{10,11} = 2/3
x10,11=2/3 组成。通过将在线附录第OS.1节中给出的程序应用于该解决方案,可以获得由三条路径构成的分解流,如图1(b)所示。
引理2:one-cut 或其连续松弛的任何解都可以分解成一组二叉树
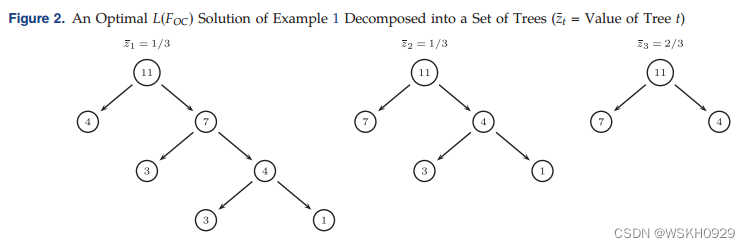
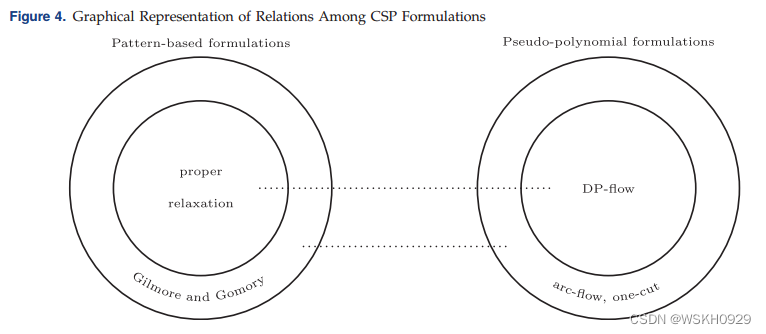
命题1: F A F F_{AF} FAF 相当于 F O C F_{OC} FOC
命题2: F D P F_{DP} FDP支配了 F A F F_{AF} FAF (因此也支配了 F O C F_{OC} FOC)
命题3: F D P F_{DP} FDP 相当于 F P R F_{PR} FPR
五、Reflect,一种改进的 Arc-Flow 公式
在本节中,我们提出了一种称为反射 ( F R E F_{RE} FRE) 的新公式,它通过仅考虑一半的 bin 容量对 CSP 实例进行建模,从而导致所需变量和约束数量的急剧减少。 F R E F_{RE} FRE 的两个主要特点如下:
- 在顶点方面, F R E F_{RE} FRE 只考虑那些对应于尺寸小于 c / 2 c/2 c/2 的部分 bin 填充加上一个额外的顶点,称为 R R R,对应于 c / 2 c/2 c/2
- 在弧方面, F R E F_{RE} FRE 考虑与 F A F F_{AF} FAF 相同的弧: (i) 将具有 d < c / 2 d< c/2 d<c/2 和 e > c / 2 e > c/2 e>c/2 的每个项目弧 ( d , e ) (d,e) (d,e)“反映”到弧 ( d , c − e ) (d, c − e) (d,c−e) 中, (ii) 删除所有 d ≥ c / 2 d ≥ c/2 d≥c/2 的项目和损失弧 ( d , e ) (d,e) (d,e),并且 (iii) 通过将 R R R 之前最右边的顶点与 R R R 连接起来创建最后一个损失弧
直观地, F A F F_{AF} FAF 中的一条路径在 F R E F_{RE} FRE 中变成了一对碰撞路径(即,两条路径都从零开始并在同一顶点结束,但两条路径中只有一条通过反射)。对于示例1, F A F F_{AF} FAF 和 F R E F_{RE} FRE 所需的弧如图5所示。 F A F F_{AF} FAF 包含六个项目弧和五个损失弧。为了构建 F R E F_{RE} FRE ,(i) 我们分别在 ( 0 , 4 ) (0, 4) (0,4) 和 ( 4 , 4 ) (4, 4) (4,4) 中反映项目弧 ( 0 , 7 ) (0, 7) (0,7) 和 ( 4 , 7 ) (4, 7) (4,7) ; (ii) 我们删除项目弧 ( 7 , 10 ) (7, 10) (7,10) 和 ( 7 , 11 ) (7, 11) (7,11) 以及损失弧 ( 7 , 10 ) (7, 10) (7,10) 和 ( 10 , 11 ) (10, 11) (10,11) ; (iii) 我们将损失弧 ( 4 , 7 ) (4, 7) (4,7) 替换为 ( 4 , R ) (4, R) (4,R) 并插入 ( R , R ) (R,R) (R,R),从而产生四个项目弧和四个损失弧。
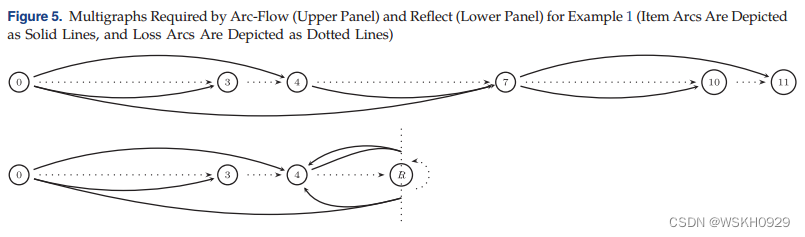
我们注意到,因为 c c c 是奇数,所以 R R R 不对应于 F A F F_{AF} FAF 中的适当节点(非正式地,它将是小数节点 5.5)。然而,在 F R E F_{RE} FRE 中需要节点 R R R 以允许某些特定模式,例如,包含大小为 4 4 4 的唯一项目的容器。我们还注意到 F R E F_{RE} FRE 基础上的想法类似于MIM 原则在图形开始和结束处的项目弧相似的意义上。然而, F R E F_{RE} FRE 走得更远,因为它承认如果所选阈值恰好等于 bin 容量的一半,则 MIM 过程中使用的双向 DP 会创建一个对称图。因此, F R E F_{RE} FRE 中使用的图可以看作是一分为二的 MIM 图。
该公式建立在多重图 G = ( V , A ) \mathscr{G}=(\mathscr{V},\mathscr{A}) G=(V,A) 上。顶点集 V \mathscr{V} V 包含 0 0 0 和 c / 2 c/2 c/2 之间的所有部分 bin 填充,对应于弧尾和弧头。
弧集合 A \mathscr{A} A 被划分为 A s \mathscr{A}_s As 和 A r \mathscr{A}_r Ar ,其中 A s \mathscr{A}_s As 表示标准弧集(即,所有那些从左到右进行的项目和损失弧,如在 F A F F_{AF} FAF 中)和 A r \mathscr{A}_r Ar 表示反射弧集(即,来自 F A F F_{AF} FAF 的那些项目弧 ( d , e ) (d,e) (d,e) 已经反映到项目弧 ( d , c − e ) (d, c − e) (d,c−e))
A s \mathscr{A}_s As 中的每条弧由三元组 ( d , e , s ) (d,e,s) (d,e,s) 定义,而 A r \mathscr{A}_r Ar 中的每条弧是由三元组 ( d , e , r ) (d,e,r) (d,e,r) 定义(请注意,可以有具有相同头部和尾部的标准弧和反射弧)。
我们在 A r \mathscr{A}_r Ar 中包含一个弧 ( c / 2 , c / 2 , r ) (c/2, c/2,r) (c/2,c/2,r) 来模拟在 c / 2 c/2 c/2 中碰撞的路径对。
我们使用 ( d , e , κ ) (d,e, κ) (d,e,κ) 表示属于 A s \mathscr{A}_s As 或 A r \mathscr{A}_r Ar 的通用弧并且 A j = { ( d , d + w j , s ) ∈ A s } ∪ { ( d , c − d − w j , r ) ∈ A r } \mathscr{A}_j = \{(d, d + w_j,s) ∈ \mathscr{A}_s\} ∪ \{(d, c − d − w_j ,r) ∈ \mathscr{A}_r\} Aj={(d,d+wj,s)∈As}∪{(d,c−d−wj,r)∈Ar} 来定义与项目类型 j j j 关联的项目弧集。
还令 δ s − ( e ) ⊆ A s ( δ r − ( e ) ⊆ A r ) δ^−_s (e) ⊆ \mathscr{A}_s (δ^−_r (e) ⊆ \mathscr{A}_r) δs−(e)⊆As(δr−(e)⊆Ar) 表示进入 e e e 的标准(反射)弧的集合。
通过将整数变量 ξ d e κ ξ_{deκ} ξdeκ 与每个 ( d , e , κ ) ∈ A (d,e,κ) ∈ \mathscr{A} (d,e,κ)∈A 相关联,我们可以将 CSP 建模为:
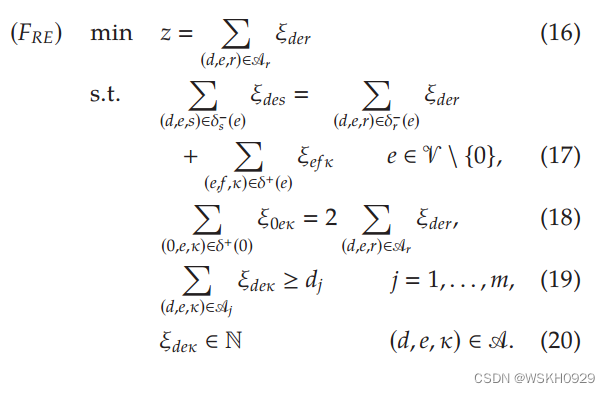
目标函数 (16) 最小化反射弧的数量,这相当于 bin 的数量。约束 (17) 确保进入节点 e 的标准弧上的流量等于从 e 发出的流量(在标准弧和反射弧上)加上进入 e 的反射弧上的流量。请注意,流量守恒约束在方程两边都有输入流量是不常见的。然而,这是我们模型正确性所必需的,因为反射弧的每个头部都必须与标准弧的头部匹配。约束条件 (18) 通过强制从零开始的流量是容器数量的两倍来施加边界条件,并且约束条件 (19) 确保满足需求。
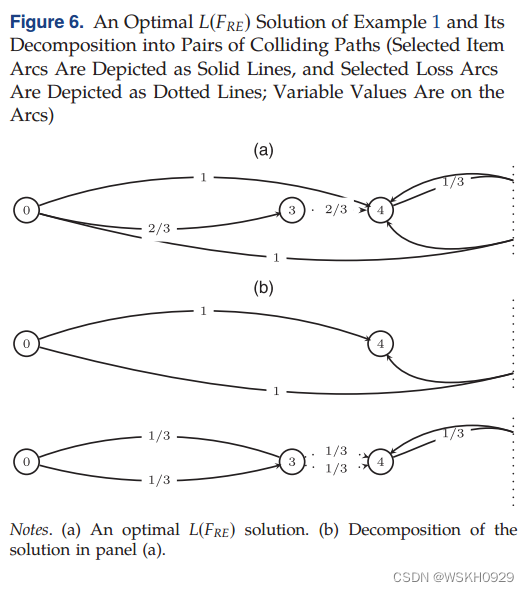
图 6(a) 中给出了示例 1 的最佳 L ( F R E ) L(F_{RE}) L(FRE) 解,其值为 4 / 3 4/3 4/3,并且可以分解为图 6(b) 中所示的碰撞路径对。
第一对由路径 ( 0 , 4 , s ) (0, 4,s) (0,4,s) 和 ( 0 , 4 , r ) (0, 4,r) (0,4,r) 组成,它们在 4 4 4 中发生碰撞,对应于包含宽度为 4 4 4 的项目和另一个宽度为 7 7 7 的项目的容器。
第二对由弧 ( 0 , 3 , s ) 、 ( 3 , 4 , s ) (0, 3,s)、(3, 4,s) (0,3,s)、(3,4,s) 和 ( 4 , 4 , r ) (4, 4,r) (4,4,r) 组成。请注意,弧 ( 0 , 3 , s ) (0, 3,s) (0,3,s) 和 ( 3 , 4 , s ) (3, 4,s) (3,4,s) 都被描绘了两次,以强调它们上的流被分开以形成两条碰撞路径:第一个是 { ( 0 , 3 , s ) , ( 3 , 4 , s ) , ( 4 , 4 , r ) } \{(0,3,s),(3,4,s),(4,4,r)\} {(0,3,s),(3,4,s),(4,4,r)} 和第二个 { ( 0 , 3 , s ) , ( 3 , 4 , s ) } \{(0,3,s),(3,4,s)\} {(0,3,s),(3,4,s)},流量均为 1 / 3 1/3 1/3 。
还要注意,如果没有反射弧进入 e e e,则 e e e 只是一个或多个面元的部分填充(例如,示例中的顶点 3 3 3);相反,如果一些反射弧进入 e e e ,则 e e e 是一个或多个箱的碰撞顶点(例如,顶点 4 4 4 )。
下面的结果证明了
F
R
E
F_{RE}
FRE 的正确性。
命题4: F R E F_{RE} FRE 模拟了CSP
命题5:任何可行的CSP图案在 F R E F_{RE} FRE 都可以用一对碰撞路径来表示,其中反射弧 ( d , e , r ) (d,e,r) (d,e,r) 具有 d ≤ e d ≤ e d≤e
我们以关于 F R E F_{RE} FRE 线性松弛的两点评论来结束这一节。
首先,让我们考虑这样一种情况,在这种情况下,不考虑项目需求来限制弧的生成,因此,允许所有 n o n p r o p e r nonproper nonproper 模式(如Gilmore和Gomory 1961年的原始方法)。在这种情况下, F A F F_{AF} FAF 相当于 F R E F_{RE} FRE 。这种等价直接来自命题4的证明,命题4指出,在这种情况下,任何有效的弧流图案都可以被转换成一对用于反射的碰撞路径,并且相反的情况也是成立的;因此,任何一对碰撞路径都可以组合起来形成一个有效的弧流模式。
其次,让我们考虑在弧生成中使用物料需求的更实际的情况下,缩小图形大小的过程。在这种情况下,我们可以得出结论,没有一种模式能支配另一种模式。为了注意到这一事实,我们提供了一个容量为 12 12 12 的箱子的最小例子;权重 9 、 6 、 3 9、6、3 9、6、3 三项;和单一需求。通过使用标准的图构建程序(例如,Coté 和 Iori 2018年的算法1),除了损失弧, F A F F_{AF} FAF 图由项目弧 ( 0 , 9 ) 、 ( 0 , 6 ) 、 ( 0 , 3 ) 、 ( 6 , 9 ) (0,9)、(0,6)、(0,3)、(6,9) (0,9)、(0,6)、(0,3)、(6,9) 和 ( 9 , 12 ) (9,12) (9,12) 组成。通过使用在线附录OS.7部分中的算法7,反射图由项目弧 ( 0 , 3 , r ) 、 ( 0 , 6 , s ) (0,3,r)、(0,6,s) (0,3,r)、(0,6,s) 和 ( 0 , 3 , s ) (0,3,s) (0,3,s) 以及连接弧 ( 6 , 6 , r ) (6,6,r) (6,6,r) 组成。在 F A F F_{AF} FAF ,由一个权重为 6 6 6 的项目和两个权重为 3 3 3 的项目组成的 n o n p r o p e r nonproper nonproper 模式允许的顺序为 ( 0 , 6 ) , ( 6 , 9 ) , ( 9 , 12 ) (0,6),(6,9),(9,12) (0,6),(6,9),(9,12) 。相反,在 F R E F_{RE} FRE 不能获得这种模式,因为没有创建标准弧 ( 3 , 6 , s ) (3,6,s) (3,6,s) (因为重量为 3 3 3 的物品的单一需求)。相反,在 F R E F_{RE} FRE ,通过使用两次与连接弧 ( 6 , 6 , r ) (6,6,r) (6,6,r) 结合的弧 ( 0 , 6 , s ) (0,6,s ) (0,6,s) ,可以获得由两个大小为 6 6 6 的物品组成的图案,但是在 F A F F_{AF} FAF 不能获得,因为弧 ( 6 , 12 ) (6,12) (6,12) 没有被创建(因为对重量为 6 6 6 的物品的单一需求)。因此, F A F F_{AF} FAF 可以包含 F R E F_{RE} FRE 禁止的 n o n p r o p e r nonproper nonproper 模式,反之亦然,因此,可能存在 L ( F A F ) < L ( F R E ) L(F_{AF})<L(F_{RE}) L(FAF)<L(FRE) 的情况,以及 L ( F R E ) < L ( F A F ) L(F_{RE})<L(F_{AF}) L(FRE)<L(FAF) 的情况。这个事实在第七节的计算结果中已经注意过几次。
5.1 Adapting Reflect 以解决大尺寸实例 : Reflect+
即使 F R E F_{RE} FRE 所使用的弧的数量相对于 F A F F_{AF} FAF 所要求的数量而言大大减少,一些具有巨大容量和许多小项目的实例仍然可能产生包含数百万个变量的模型,因此太难处理。为了解决这个问题,我们提出了一些上下界技术,并把它们嵌入到一个新的算法 reflect+ 中。
5.1.1 列生成
我们首先通过标准的列生成技术求解 L ( F P R ) L(F_{PR}) L(FPR) ,即(2)的线性松弛。
简化的主问题用单位矩阵初始化,并作为线性规划求解,以获得每个项目类型 j j j 的对偶变量值 π j π_j πj
通过求解背包子问题,找到具有负缩减成本的列,并将其添加到运行中的主问题中,直到达到最优证明。
对于子问题,我们使用Martello等人(1999)的 combo ,它解决了二进制背包问题。
我们首先使用 combo 作为启发式方法,向它提供 m m m 个项目 j j j ,利润 π j π_j πj 和权重 w j w_j wj (每个项目类型只有一个项目)。
如果这种尝试未能找到负的降低成本列,我们通过向其提供整个项目集,调用二进制扩展来使用 combo 精确求解(例如,参见Vanderbeck和Wolsey 2010)。
每个项目类型 j j j 有需求的 d j d_j dj 由 ⌊ log d j ⌋ + 1 \left\lfloor\log d_j\right\rfloor+1 ⌊logdj⌋+1 项表示,其中第一项 k = 0 , 1 , . . . , ⌊ log d j ⌋ + 1 k = 0,1,...,\left\lfloor\log d_j\right\rfloor+1 k=0,1,...,⌊logdj⌋+1 的利润为 2 k π j 2^kπ_j 2kπj ,权重为 2 k w j 2^kw_j 2kwj ,最后一项 l = ⌊ log d j ⌋ l=\left\lfloor\log d_j\right\rfloor l=⌊logdj⌋的利润为 ( d j − ( 2 l − 1 ) ) π j (d_j-(2^l- 1))π_j (dj−(2l−1))πj ,权重为 ( d j − ( 2 l − 1 ) ) w j (d_j-(2^l- 1))w_j (dj−(2l−1))wj 。
第一种试探的目的是避免具有许多小项的模式,这些小项可能出现在早期的列生成迭代中,并稍微恶化我们连续的上限过程。
设 P L P ⊆ P P_{LP} ⊆ P PLP⊆P 表示为达到线性最优而生成的列的集合。从该信息获得上界的经典方法是仅用列的集合 P L P P_{LP} PLP 来解决受限主问题的整数问题。
这种程序通常被称为限制性主启发式,易于实施,但可能产生低质量的解决方案(例如,见Sadykov等人2019年)。
在这里,我们提出了一个简单而有效的改进,包括在只包含 P L P P_{LP} PLP 产生的弧的多重图上求解 F R E F_{RE} FRE。
具体来说,我们从空的 F R E F_{RE} FRE 多重图开始,通过不增加权重来考虑包含在列 p p p 中的所有项目,并且按照该顺序为每个项目生成单个弧(使用在命题5的证明中概述的算法)。
我们对所有 p ∈ P L P p ∈ P_{LP} p∈PLP 重复该过程,然后在简化的实例上求解 F R E F_{RE} FRE。我们的方法受以下因素的激励。
备注1:设 z ( F P R ( P L P ) ) z(F_{PR}(P_{LP})) z(FPR(PLP)) 是仅包含 P L P P_{LP} PLP 中的列的受限 F P R F_{PR} FPR 的最优解值, z ( F R E ( P L P ) ) z(F_{RE}(P_{LP})) z(FRE(PLP)) 是仅包含由 P L P P_{LP} PLP 中的列产生的弧的受限 F R E F_{RE} FRE 的最优解值;那么, z ( F R E ( P L P ) ) ≤ z ( F P R ( P L P ) ) z(F_{RE}(P_{LP}))≤ z(F_{PR}(P_{LP})) z(FRE(PLP))≤z(FPR(PLP)) 。
这个评论来自于这样一个事实:所有的模式 p ∈ P L P p ∈ P_{LP} p∈PLP 都可以由 F R E F_{RE} FRE 产生,但是 F R E F_{RE} FRE 也可以产生不属于 P L P P_{LP} PLP 的模式。例如,考虑图5的下面板。
这些弧可以通过模式 ( 1 , 0 , 1 ) (1,0,1) (1,0,1) 和 ( 0 , 1 , 1 ) (0,1,1) (0,1,1) 的映射来获得,但是 F R E F_{RE} FRE 也有可能通过弧 { ( 0 , 4 , r ) , ( 0 , 4 , s ) } \{(0,4,r),(0,4,s)\} {(0,4,r),(0,4,s)} 来产生合适的模式 ( 1 , 1 , 0 ) (1,1,0) (1,1,0) 以及通过弧 { ( 0 , 4 , s ) , ( 4 , 4 , r ) , ( 0 , 4 , s ) } \{(0,4,s),(4,4,r),(0,4,s)\} {(0,4,s),(4,4,r),(0,4,s)} 来产生非合适的模式 ( 0 , 2 , 1 ) ; ( 0 , 1 , 2 ) (0,2,1);(0,1,2) (0,2,1);(0,1,2) 通过弧 { ( 0 , 4 , s ) , ( 4 , 4 , r ) , ( 0 , 3 , s ) , ( 3 , 4 , s ) } \{(0,4,s),(4,4,r),(0,3,s),(3,4,s)\} {(0,4,s),(4,4,r),(0,3,s),(3,4,s)} ;和 ( 0 , 0 , 3 ) (0,0,3) (0,0,3) 通过弧 { ( 0 , 3 , s ) , ( 3 , 4 , s ) , ( 4 , 4 , r ) , ( 0 , 3 , s ) , ( 3 , 4 , s ) } \{(0,3,s),(3,4,s),(4,4,r),(0,3,s),(3,4,s)\} {(0,3,s),(3,4,s),(4,4,r),(0,3,s),(3,4,s)} ,从而提供大量可能的启发式解。
在我们的实现中,我们首先将 P b a s e ⊆ P L P P_{base} ⊆ P_{LP} Pbase⊆PLP 计算为具有在线性解决方案中取正值的相关变量的列的子集。然后,我们计算 z ( F R E ( P b a s e ) ) z(F_{RE}(P_{base})) z(FRE(Pbase)) ,这通常很快,如果需要,再计算 z ( F R E ( P L P ) ) z(F_{RE}(P_{LP})) z(FRE(PLP)) 。
5.1.2 节点去激活和对偶切割
我们解决 L ( F R E ) L(F_{RE}) L(FRE) 与完整的弧集,然后使用其线性解 ξ ˉ \bar{ξ} ξˉ 建立非活动顶点集 V n = { d ∈ V : ∄ ξ ˉ n ( d , e , κ ) > ϵ } \mathscr{V}_n = \{d ∈\mathscr{V} : ∄\ \bar{ξ}_n (d,e,κ) >\epsilon \} Vn={d∈V:∄ ξˉn(d,e,κ)>ϵ} 。然后,我们用附加约束来求解 F R E F_{RE} FRE:
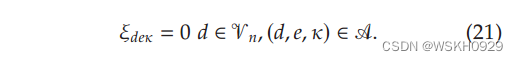
约束(21)使得模型的解更快,但是可能移除太多可行解。
我们通过实验注意到,通过允许将一些大项目拆分成较小的项目,可以找到更好的解决方案。
为此,我们创建一组可能变换的集合 T = ( i , j , k ) T=(i,j,k) T=(i,j,k) ,其中 i , j , k = 1 , . . . , m ; i < j < k ; w i = w j + w k i,j,k = 1,...,m \ ;\ i<j<k \ ;\ \ w_i=w_j+w_k i,j,k=1,...,m ; i<j<k ; wi=wj+wk
我们为 ( i , j , k ) ∈ T (i,j,k) ∈ T (i,j,k)∈T 创建一族整数变量 t i j k t_{ijk} tijk ,每个变量计算一个项 i i i 被转化为项 j j j 和 k k k 的次数。
然后,我们将(19)替换为
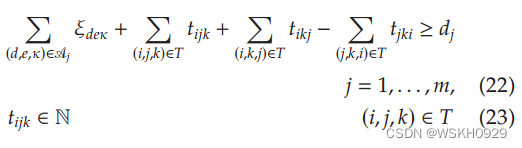
并求解模型(16)-(18)和(20)-(23)。这种方法让人想起Valério de Carvalho (2005)的对偶切割。注意,( 22)和(23)也可以在
F
R
E
F_{RE}
FRE 直接使用。然而,因为模型的主要问题是它的大小,所以添加额外的约束和变量似乎没有前途。
5.1.3 弧失活
我们的第三个启发式算法试图找到一个正好值为 L = ⌈ L ( F R E ) ⌉ L = \lceil L(F_{RE})\rceil L=⌈L(FRE)⌉ 的解
为了这个目标,我们集合在一起 A z \mathscr{A}_z Az 所有降低成本大于 L − L ( F R E ) + ϵ L-L(F_{RE}) +\epsilon L−L(FRE)+ϵ 的弧,并通过设置来限制 F R E F_{RE} FRE 模型
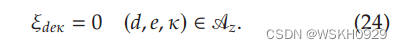
事实上,选择一个或多个弧
A
z
\mathscr{A}_z
Az 意味着解的值大于
L
L
L 。然后我们求解模型(16)–( 20)和(24)。
如果没有找到值为 L L L 的解,我们将 L L L 增加1,更新 A z \mathscr{A}_z Az ,并迭代。
注意,如果MIRUP猜想成立,那么该过程最多迭代一次。
由此产生的reflect+算法按照我们给出的顺序利用了这些技术。
算法1中给出了一个非正式的伪代码。
尽管没有明确说明,但只要上限值和下限值相等,该算法显然就会停止。每次将模型作为MILP求解时,只允许有限的执行时间,如下文第8节所述。

我们注意到,本节介绍的技术也可以用于改进 F A F F_{AF} FAF 而不是 F R E F_{RE} FRE ,尽管这需要不同的实现。
六、可变大小的BPP
七、带有项目碎片的BPP
八、计算结果
在这一节中,我们通过计算评估提出的技术,并与现有的文献进行比较。
我们所有的实验都是在英特尔至强处理器3.10 GHz、8 GB内存(www .passmark.com上的CPU passmark indicator = 6,594)上执行的,使用Gurobi 6.5作为MILP解算器。
所有测试都是使用单个内核,并通过在MILP解算器配置中将线程数设置为1(线程数= 1)来执行的。
就参数化而言,对于我们的代码,我们选择Presolve = 1(保守)和Method = 2(内点法)。正如布兰多和佩德罗索(2016)所提到的,这些参数可以产生比默认值好得多的结果。
由于尝试了大量实例,在下表中,我们主要提供每个算法和每组实例的聚合信息,包括以下两个主要指标:
- #opt =行中实例中已证实的最优解的总数
- sec =该行中所有实例经过的平均CPU秒数
表格中以粗体突出显示了每行中#opt的最佳值。在计算sec时,我们考虑所有实例的整个时间限制值,这些实例的执行使用了整个时间限制,或者由于内存限制而提前中断。
标有 total/average 的行报告由两行或多行组成的组的total #opt和average sec值。
8.1 关于BPP和CSP的结果
我们在最著名和最具挑战性的BPP和CSP基准集上测试了我们的算法。
- Classical : 在过去几十年的各种文章中提出的一组1,615个实例,具有多样化的特征(完整的描述见Delorme等人2016)
- GI : Gschwind和Irnich (2016年)提出的四组60个实例,涉及的bin容量高达1,500,000
- AI/ANI : Delorme等人(2016年)提出的两组100个具有挑战性的实例
本节的实例和算法可从Delorme等人(2018)的BPPLIB获得。我们首先评价 F R E F_{RE} FRE 对经典 F A F F_{AF} FAF 的改进。
表1提供了通过在3,600秒的时限下运行两种制剂获得的结果。表中的前两列标识了基准集和相应的实例数量。
除了#opt和sec,该表给出了变量的平均数(nb.var.)和约束(nb.cons)在模型中和它们的连续松弛值(除了GI实例,对于GI实例,该信息在执行结束时并不总是可用的)。
值得注意的是, F R E F_{RE} FRE 在#opt和sec两方面都优于 F A F F_{AF} FAF 。
这可以通过reflect获得的大幅变量和约束缩减来解释:平均81.2%的变量缩减(从AI 400的64.5%到Scholl 3的98%)和平均64.1%的约束缩减(从Scholl 1的31.9%到GI BA的92.2%)。
然而,即使有了这些显著的减少,reflect也不能处理建模GI AB和GI BB实例所需的数百万个变量和数十万个约束。
就连续弛豫而言,我们观察到 L ( F A F ) L(F_{AF}) L(FAF) 和 L ( F R E ) L(F_{RE}) L(FRE) 所取的值非常相似。
在经典的例子中,差异平均只有0.01(有利于 F A F F_{AF} FAF )。
在这1615例中, F A F F_{AF} FAF 在50例中具有更好的连续松弛值(最大差异为0.5), F R E F_{RE} FRE 在15例中具有更好的连续松弛值(最大差异为0.13),在其余的例子中两个值相等。
我们现在分析 reflect+ 的性能。我们首先关注文献中多次采用的经典限制性主试探法(用较少的列解决 F P R F_{PR} FPR 问题)和reflect+中使用的前两种新试探法(用较少的弧解决 F R E F_{RE} FRE 问题)之间的差异。表2提供了在60秒的时间限制内,仅考虑来自 P b a s e P_{base} Pbase 或 P L P P_{LP} PLP(见第5.1节)的列/弧,运行 F P R F_{PR} FPR 和 F R E F_{RE} FRE 得到的结果。除了#opt和sec之外,表提供了执行达到时间限制(t.l .)的次数,以及与最佳已知下限(a.g. = U - L)的平均绝对差距。
表2显示,当用于一组有限的模式时, F R E F_{RE} FRE 大大优于 F P R F_{PR} FPR 。有时, F P R ( P b a s e ) F_{PR}(P_{base}) FPR(Pbase) 和 F P R ( P L P ) F_{PR}(P_{LP}) FPR(PLP) 都很快,但往往会以次优的解决方案结束(例如onWaescher),而其他一些时候,他们不会在时限内完成(例如在Scholl 2上)。
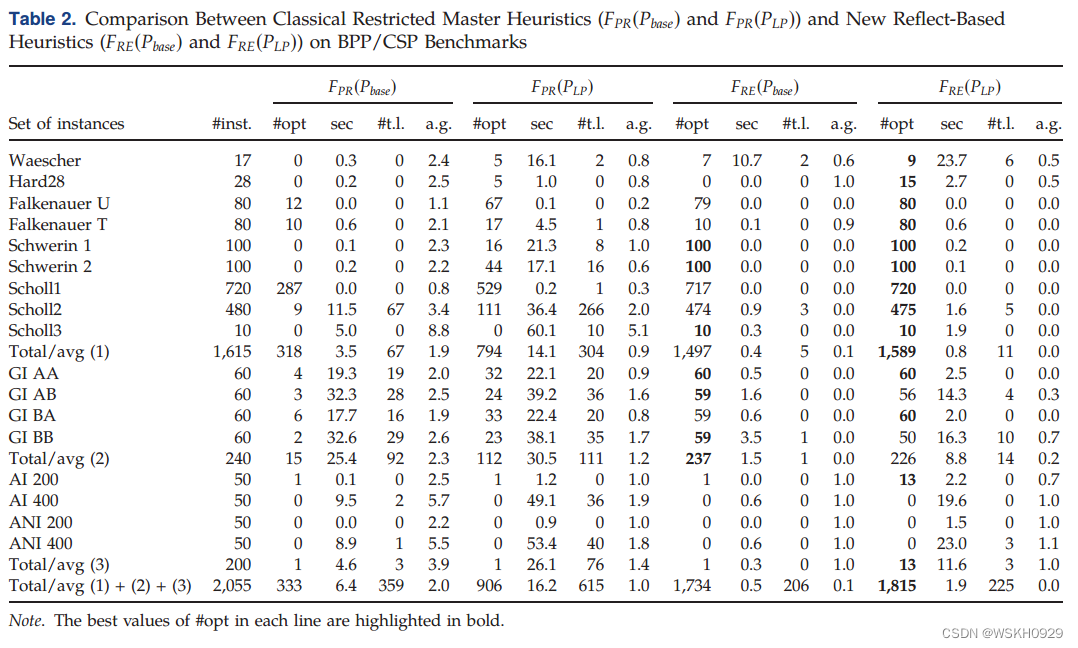
F R E ( P b a s e ) F_{RE}(P_{base}) FRE(Pbase) 和 F R E ( P L P ) F_{RE}(P_{LP}) FRE(PLP) 都获得了很好的结果,因为它们在很短的时间内解决了大多数实例的最优解,在未解决的实例上实现了很小的平均差距。
在 F R E ( P b a s e ) F_{RE}(P_{base}) FRE(Pbase) 和 F R E ( P L P ) F_{RE}(P_{LP}) FRE(PLP) 之间没有明显的优势: F R E ( P b a s e ) F_{RE}(P_{base}) FRE(Pbase) 更快,尤其是在容量非常大的情况下(例如GI AB),但是 F R E ( P L P ) F_{RE}(P_{LP}) FRE(PLP) 更经常地终止于已证明的最优解(例如Falkenauer T)。
注意,没有算法能够为困难的AI/ANI实例提供好的结果,这需要更高级的技术。
表3将reflect和reflect+与BPP/CSP文献中的最佳算法进行了比较。
基于德洛姆等人(2016年)的结果,我们选择了在很大程度上主导其他10种精确方法的两种方法,即别洛夫和谢绍尔(2006年)的分支-切割-定价(Branch-and-cut-and-price),下文简称 Belov,以及布兰多和佩德罗索(2016年)的VPSolver。我们还添加了我们对Coté和ˇIori (2018)MIM方法的实施。我们在机器上运行了这三种方法的代码。
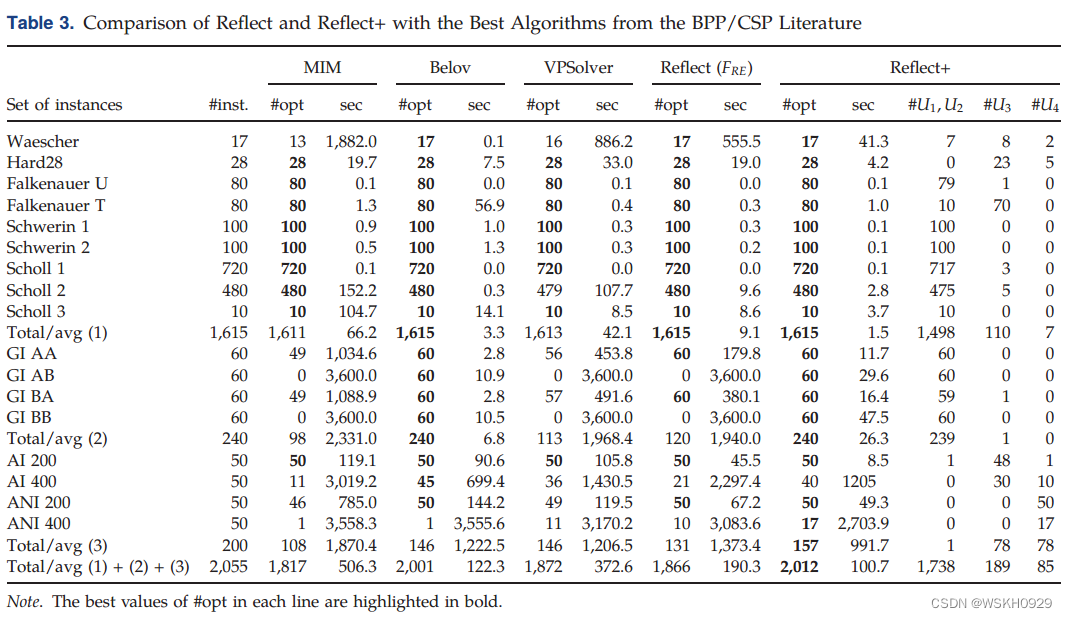
根据规范要求,Cplex(版本12.6)用于Belov,Gurobi 6.5用于VPSolver。我们对MIM的重新实现使用了Gurobi 6.5和用于arc-flow和reflect的相同参数配置。除了#opt和sec,表3还提供了reflect+实例被
F
R
E
(
P
b
a
s
e
)
F_{RE}(P_{base})
FRE(Pbase) 和 $F_{RE}(P_{LP}) KaTeX parse error: Expected 'EOF', got '#' at position 2: (#̲U1,U2)、F_{RE}$+(21)-(23)(# U3)和主算法循环(#U4)接近最优的次数。我们为reflect+找到的最佳配置如下:对于标准实例
(nb.var. 多了10倍 nb.cons.低于100万),我们给了U1最多60秒,U3最多1200,U4剩余时间;对于其他非常大的实例,我们给了3600秒来计算U1,剩下的时间(如果有的话)给了U2,然后可能是U4。
表3显示了reflect+的行为非常令人满意,并且附加的技术有助于改进仅由reflect获得的结果。
虽然U1和U2对于前两个基准集是有效的,但是U3和U4对于第三个困难集是有用的。平均而言,在最优解的数量和时间方面,reflect+始终优于VPSolver和MIM,尤其是在困难的情况下(Waescher、GI AB和BB以及AI 400)。
与Belov相比,reflect+在AI 400实例(问题是找到好的启发式解决方案)上不太强大,但在ANI 400实例(很难将下限提高到最优值)上更好,总体而言,它以稍小的计算量找到了11个更经证明的最优解决方案。
8.2 VSBPP的结果
8.3 BPPIF的结果
九、结论和未来研究
- 由于混合整数线性规划求解器性能的显著提高,伪多项式模型最近已成为许多组合优化问题求解的有用工具。这为开发新的有效的组合技术和设计专用的解决方案算法提供了有趣的机会。
- 在我们的工作中,我们研究了经典BPP和下料问题的伪多项式模型。
- 我们给出了主要公式之间的优势和等价关系的完整概述。
- 然后,我们介绍了一个公式,它模拟了一个简化网络上的BPP实例,其中源到宿的路径被成对的冲突路径所代替。
- 我们通过使用基于列生成、双重切割和试探法的技术改进了该公式的计算性能,并通过将它们适用于两个相关的BPP推广,即可变大小的BPP和具有项目碎片的BPP,展示了所提出的方法的易复制性。
- 大量的计算结果证明了我们的算法是非常有效的,改进了现有的文献,并为许多以前未解决的基准实例提供了最优解。
- 对伪多项式模型的研究是当前非常感兴趣的,因为它可以帮助改进许多实际感兴趣的决策问题中的现有技术结果。
- 相关应用可能出现在一维切割和打包[例如,在具有松散箱容量的问题中(Ceselli和Righini,2008年),可重复使用的剩菜(Arbib等人,2002年),或基数约束(Sadykov和Vanderbeck,2013年)],以及二维切割和打包[例如,作为原始分解方法中的主问题(如Coté等人,2014年和Delorme等人,2017年)]。
- 然而,它们也可能出现在资源约束和/或优先约束问题、有能力约束的车辆路径区域以及不同目标函数下的单机和多机调度问题中。在实践中,在许多这样的组合优化问题中,容量扮演着重要的角色。
- 多目标优化也可以通过施加不同的网络弧线上的利润/成本,并使用路径重构算法来导出Pareto最优解。改进现有模型的新的先进技术的发展也是很有意义的。
- 对于BPP,我们的伪多项式模型尤其受到具有大箱容量和大量轻量级项目的实例的压力,事实上,尽管应用了几十种算法,只有400个项目的实例仍未解决。
- 因此,未来的研究设想既设计新的应用模型,又改进现有的模型。