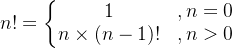算法——深度优先搜索（DFS）

DFS

• 思路：
  • 从初始状态出发，下一步可能有多种状态；选其中一个状态深入，到达新的状态；直到无法继续深入，回退到前一步，转移到其他状态，然后再深入下去。最后，遍历完所有可以到达的状态，并得到最终的解。
  • DFS通常使用递归来实现
• 弊端：
  • 递归容易超时
• 大部分DFS搜索的题目都需要用到回溯的思路，其难度主要在于扩展子结点时如何构造停止递归并返回的条件。 

递归

•  递归方法就是直接或间接地调用其自身

•  注意：

  • 避免进入死循环

  • 容易超时

    • 递归 <——> 非递归，相互转化

回溯法

• 回溯法是一种采用深度优先方式进行搜索的算法，当搜索到某一步时，如果发现原先的选择不是最优选择或者达不到目标，就退回一步重新选择。
• 剪枝函数：（在回溯中用于减少子结点扩展的函数）
  • 1、约束函数：是问题的可行解吗？
  • 2、限界函数：确定是问题的可行解，但，是问题的最优解吗？
• 解题步骤：
  • 1、如何递归
  • 2、如何剪枝与回溯

一、计算阶乘（递归）

阶乘函数：

比如

• 3！=6
  • 3！= 3*2*1 = 6
• 4！=24
  • 4！= 4*3*2*1 = 24
• 5！=120
  • 5！= 5*4*3*2*1 = 120

分析：

• 

package no1_1;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n = input.nextInt();
		System.out.println(factorial(n));
	}
	public static int factorial(int n) {
		if(n==0) {
			return 1;
		}else {
			return n*factorial(n-1);
		}
	}
}

二、数字游戏（回溯）

　　给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。
　　例如:
　　3 1 2 4
　　4 3 6
　　7 9
　　16
　　现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。

分析：

• 
• 

package no1_1;

import java.util.Scanner;
 
public class Main {
	//main()方法是静态方法，它只能调用静态方法，所以dfs()也是静态方法
	//因为两个方法都是静态方法，所以它们共用的属性sum,N等都得是静态的
	static int sum;
	static int N;
	static int arr1[];
	static boolean flag = true;
 
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		N = input.nextInt();
		sum = input.nextInt();
		int array[] = new int[N];
		int usedArray[] = new int[N + 1];
		//开始递归
		dfs(0, array, usedArray, flag);
	}
 
	public static void dfs(int step, int arr[], int usedArray[], Boolean flag) {
		//首先检查当前步数是否等于N，如果是，则表示已经生成了一个完整的排列(最顶层，有N个数的数组)
		if (step == N) {
			//复制该排列到新数组中
			int arr1[] = new int[N];
			for (int i = 0; i < N; i++) {
				arr1[i] = arr[i];
			}
			//从上往下，计算该排列最终得到的数字
			for (int i = 1; i < N; i++) {
				for (int j = 0; j < N - i; j++) {
					arr1[j] = arr1[j] + arr1[j + 1];
				}
			}
			//某排列计算出的数字与题目符合
			if (arr1[0] == sum) {
				//把该排列输出到控制台
				for (int x : arr) {
					System.out.print(x + " ");
				}
				//停止递归
				flag = false;
				//回溯，但不再递归
				return;
 
			} else
				//条件不满足，
				//回溯，继续递归生成下一步的排列
				return;
		}
		//继续递归，生成可能的排列
		if (flag == true) {
			//最初序列arr[i]，为1～N的一个排列
			//在递归生成排列时，使用usedArray数组来标记已经使用过的数字，避免重复使用
			for (int i = 1; i <= N; i++) {
				if (usedArray[i] == 0) {
					arr[step] = i;
					usedArray[i] = 1;
					dfs(step + 1, arr, usedArray, flag);
					usedArray[i] = 0;//取消标记
				}
			}
		}
		return;
	}
}
 

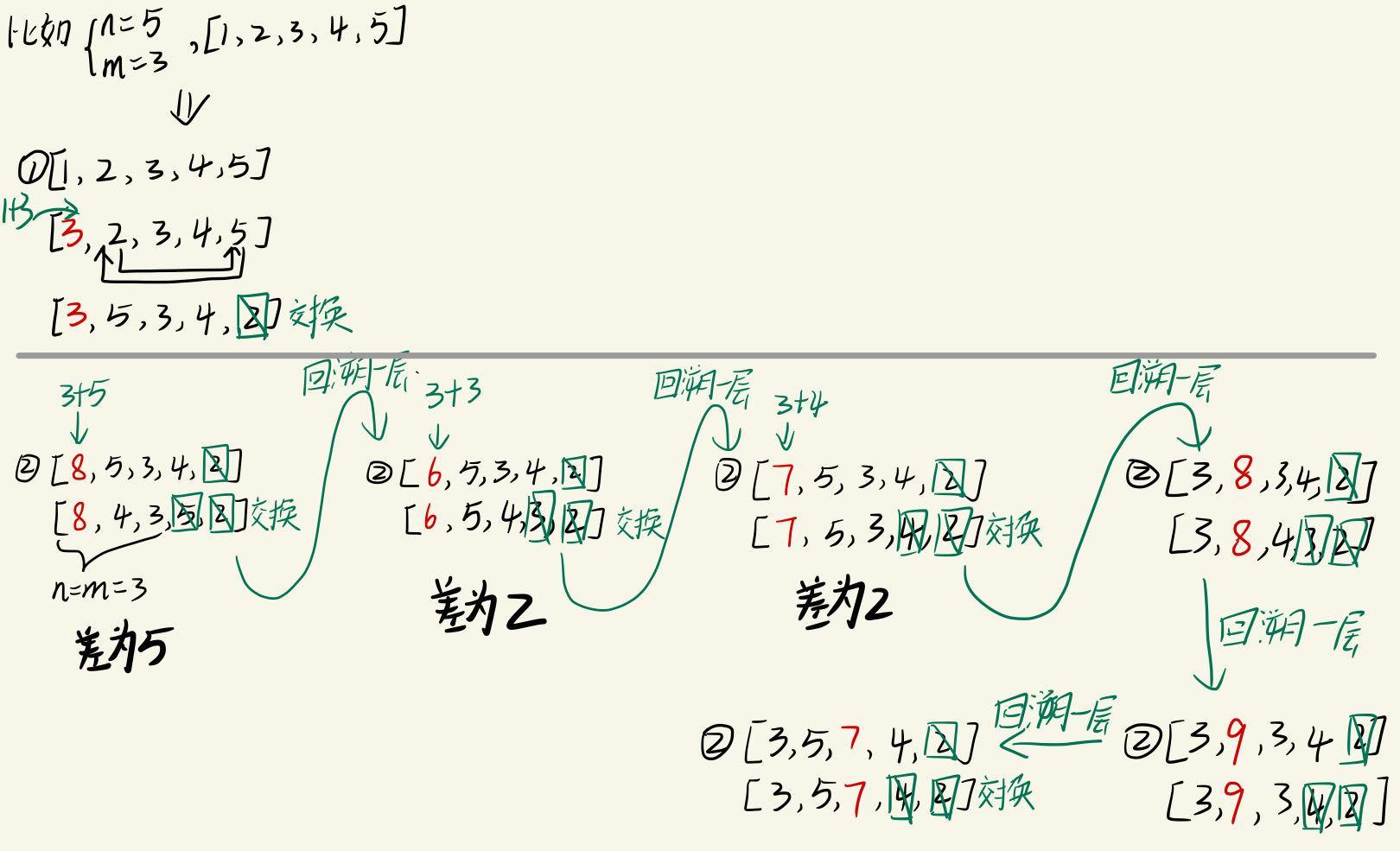
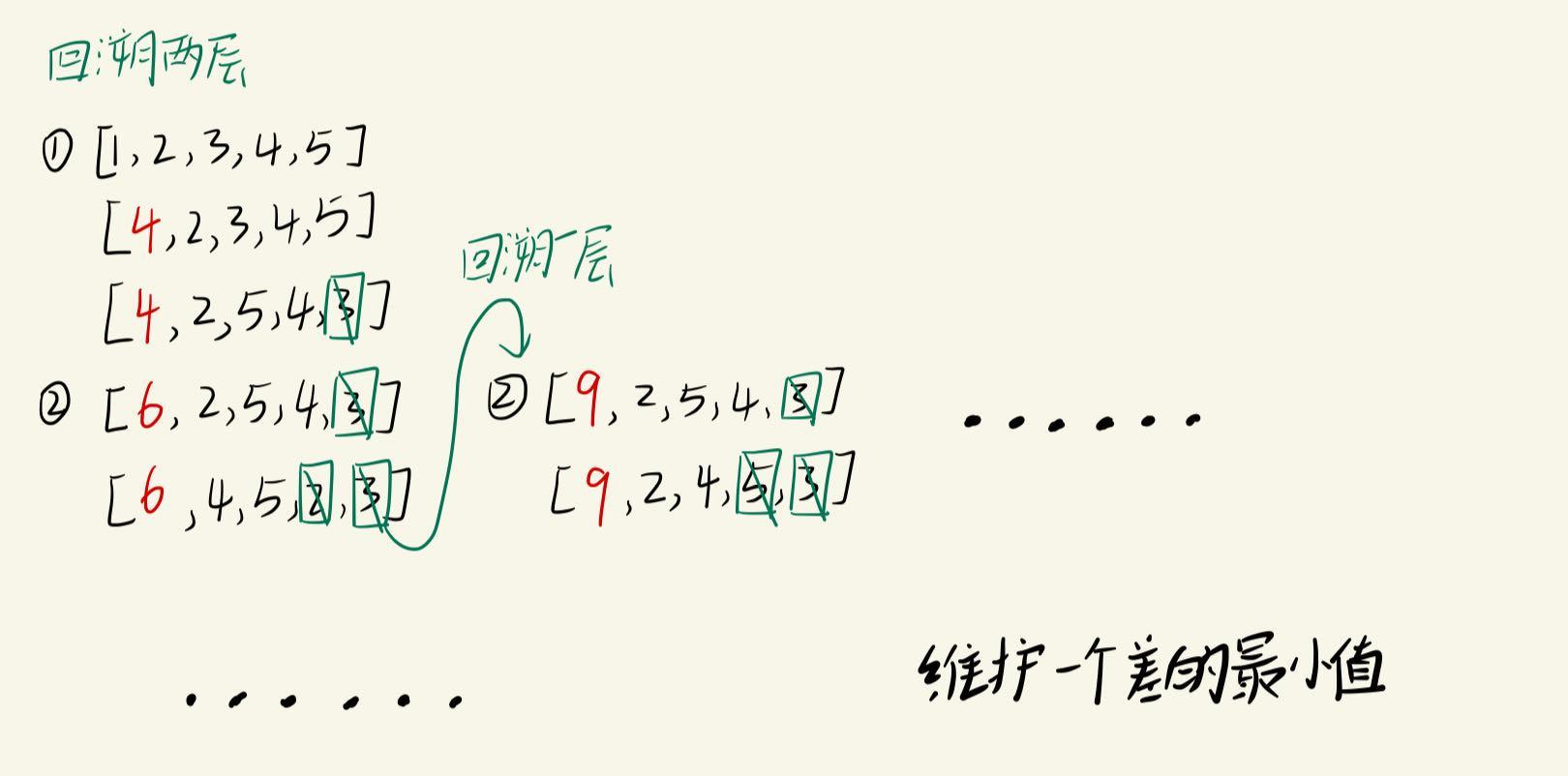
三、粘木棍（DFS）

分析：

• 
• 

package no1_1;
import java.util.*;
public class Main {
	static int n,m,result=Integer.MAX_VALUE;
	static int[] array;
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        n=input.nextInt();
        m=input.nextInt();
        array=new int[n];
        for(int i=0;i<n;i++) {
        	array[i]=input.nextInt();
        }
        dfs(n);
        System.out.println(result);
    }
    public static void dfs(int n) {
    	if(n==m) {//到达底部，先验证这次分组是否正确，如果不正确就回溯
            //不用Arrays.sort()方法找最大值和最小值，是为了方便回溯，如果随便改变了数组元素的顺序，就无法正常回溯了
    		int min=Integer.MAX_VALUE,max=Integer.MIN_VALUE;
    		for(int i=0;i<m;i++) {
    			if(array[i]<min) min=array[i];
    			if(array[i]>max) max=array[i];
    		}
    		result=Math.min(result, max-min);//维护一个最小的差值
    		return ;//停止递归，返回
    	}
    	for(int i=0;i<n;i++) {
    		for(int j=i+1;j<n;j++) {
    			array[i]+=array[j];//合并元素
    			swap(j,n-1);//将废弃的元素丢到数组后面
    			dfs(n-1);//数组长度减一
    			swap(j,n-1);//回溯，交换回来
    			array[i]-=array[j];//把合并的两个元素和拆开
    		}
    	}
    }
    //交换函数
    public static void swap(int a,int b) {
    	int temp=array[a];
    	array[a]=array[b];
    	array[b]=temp;
    }
}