哈夫曼树到最佳归并树python实现

Huffman树

  哈夫曼树通常应用在编码方面，主要为了解决权重或者说频次上的最佳问题。一般来说一个好的编码方案会大大提升通信的效率，降低延迟！如果把编码中出现的频次当作权重，则越是频繁出现的通信语句应当是短小的，而不常用的语句应当是较为长的，这样才能保证我们通信中用的较多的语句占用不大的带宽。
  其步骤如下：

• 给定n个权值w1,w2,w3…
• 将每个权值分别作为一个二叉树的根节点，构成森林F，按照权重排序
• 从F中选两个权重最小的节点，作为一个新节点的左右孩子节点，并且当前权重赋值为两个子节点权重之和
• 删除选中的两个子节点，并将第三步生成的新节点加入F中对应的位置。重复上一步和当前一步直到F中仅剩一棵树即可。

以四个权重7，5，2，4为例：

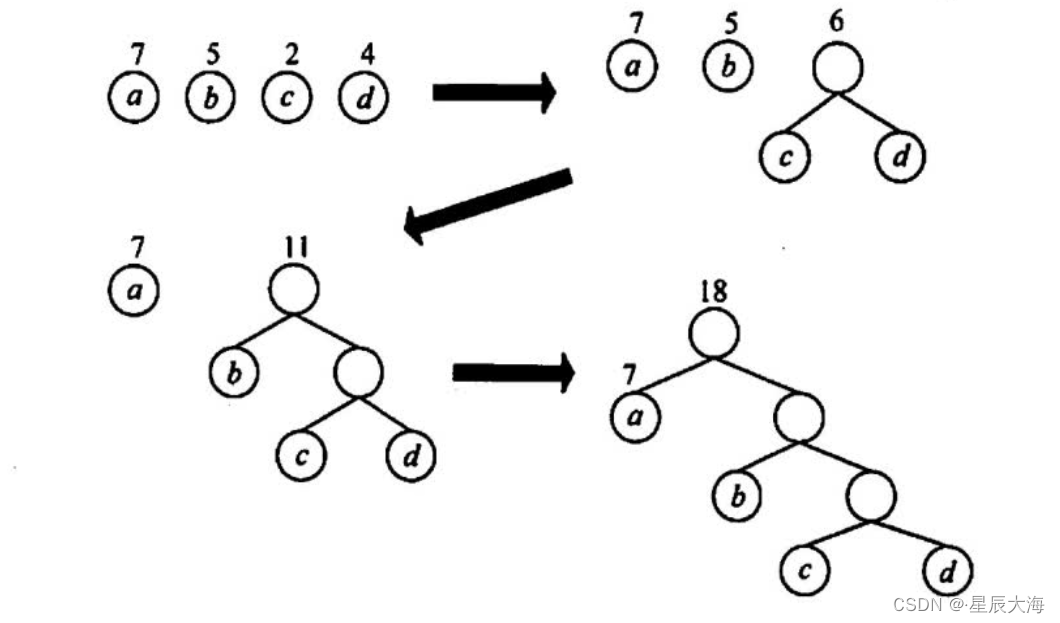
上图来自王道数据结构。

Huffman树的实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


def huffman(weight):
    tree_list = [TreeNode(val=i) for i in sorted(weight, reverse=True)]
    while len(tree_list) > 1:
        left, right = tree_list.pop(), tree_list.pop()
        new_node = TreeNode(left.val + right.val, left, right)
        for i in range(len(tree_list) - 1, -1, -1):
            if new_node.val < tree_list[i].val:
                break
        tree_list.insert(i+1, new_node)
    return tree_list[0]


if __name__ == '__main__':
    weight = [5, 2, 4, 7]
    ans = huffman(weight)

最佳归并树

  我们都知道正常的哈夫曼树只有度为0的节点和度为2的节点，同理最佳归并树也是这样，假设有一个k叉的归并树，那么这棵树应该只有度为0和度为k的节点，总结点数为$k{n}_k+0n_0+1=n_k+n_0$可以得出$n_0=(k-1)n_k+1,n_k=(n_0-1)/(k-1)$如果整除则可以说明给定的权重个数正好可以构成归并树，否则说明有$(n_0-1)\%(k-1)个n_0$节点是多余的，此时应当使用一个$n_0$节点充当$n_k$节点，然后再补充$k-1-(n_0-1)\%(k-1)$个$n_0$节点，并将新补充的节点权重置为0即可。

class TreeNode:
    def __init__(self, val=0, left=None, right=None, children=None):
        self.val = val
        self.left = left
        self.right = right
        self.children = children
def omt(weight, k):
    u = (len(weight) - 1) % (k - 1)
    add = k - u - 1
    tree_list = [TreeNode(val=i) for i in sorted(weight, reverse=True)]
    for i in range(add):
        tree_list.append(TreeNode())
    while len(tree_list) > 1:
        temp = [tree_list.pop() for _ in range(k)]
        new_node = TreeNode(val=sum([i.val for i in temp]), children=temp)
        for i in range(len(tree_list) - 1, -1, -1):
            if new_node.val < tree_list[i].val:
                break
        tree_list.insert(i+1, new_node)
    return tree_list[0]

if __name__ == '__main__':
    weight = [2, 3, 6, 9, 17, 18, 12, 24]
    ans = omt(weight, 3)