AxMath使用教程+常用符号与公式（持续更新中）

前言

这两天学了学Latex，主要是为了以后写毕业论文做铺垫，而且Latex在数学公式这一方面，要比Word方便许多，于是我就下载了一款国产的公式编辑器——AxMath。永久会员不贵，只要36元，而且软件很好用，我选择支持国产。因为我是学通信的，可能整理的一些通信相关的公式和符号较多。

---

---

面板介绍

我感觉常用的其实就这俩功能，如果熟练起来的话，基本不需要鼠标操作。没学这些之前一直有一个误区就是觉得Latex要会写代码，其实学了之后才发现，基本不需要自己写，套模板和复制就足够了。

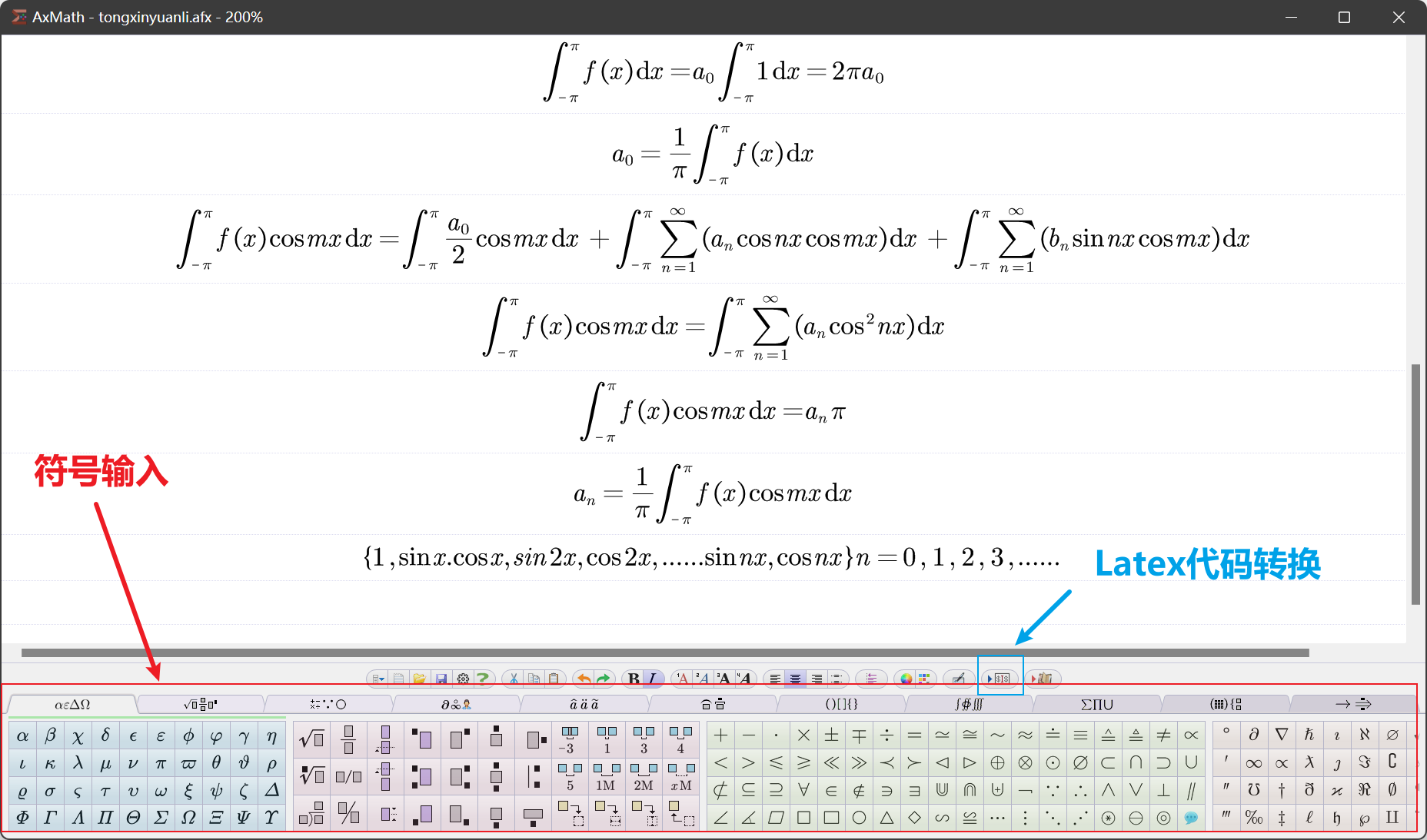
点击Latex代码转换

这个好处就是可以根据上面写的公式来学习代码是怎么写的

---

输入公式

渲染

两个$中间夹起来表示渲染Latex

$$ 要渲染的内容 $$

基本运算符号

名称	AxMath	渲染后
加	+	$$+$$
减	-	$$-$$
乘	\cdot	$$\cdot$$
除	\div	$$÷$$
正负	\pm	$$\pm$$

\cdot表示点乘,一般不写 *作为乘号

分数

普通输入	AxMath	渲染后
1/2	\frac{1}{2}	$$\frac{1}{2}$$

解读：\frac{分子}{分母}

根号

名称	AxMath	渲染后
根号	\sqrt{2}	$$\sqrt{2}$$
多次根号	\sqrt[3]{2}	$$\sqrt[3]{2}$$

解读：
	\sqrt{被开方数}
	\sqrt[开几次根]{被开方数}

上划线与下划线

名称	AxMath	渲染后
上划线	\overline{a}	$$\overline{a}$$
下划线	\underline{a}	$$\underline{a}$$

等式关系

名称	AxMath	渲染后
等于	=	$$=$$
不等于	\ne	$$\ne$$
约等于	\approx	$$\approx$$
小于	<	$$<$$
大于	>	$$>$$
小于等于	\leqslant	$$⩽$$
大于等于	\geqslant	$$⩾$$

换行与空格

普通输入	AxMath	渲染后
\\(双反斜杠)	\frac{1}{2} \\ \frac{1}{2}	$$\begin{gathered} \frac{1}{2} \\ \frac{1}{2} \end{gathered}$$
~(波浪线)	\frac{1}{2} ~~~~ \frac{1}{2}	$$\frac{1}{2}\frac{1}{2}$$

常用三角函数

普通输入	AxMath	渲染后
sin	sin	$$\sin$$
cos	cos	$$\cos$$
tan	sin	$$\tan$$
arcsin	arcsin	$$\mathrm{arc}\sin$$
arccos	arccos	$$\mathrm{arc}\cos$$
arctan	arctan	$$\mathrm{arc}\tan$$
sec	sec	$$\sec$$
cot	cot	$$\cot$$
csc	csc	$$\csc$$

括号

名称	AxMath	渲染后
小括号	()	$$()$$
中括号	[]	$$[]$$
大括号	{}	{ } \left\{ \right\} {}
多行小括号	\left( \begin{array}{c}1\2\3\\end{array} \right)	$$\left(\begin{array}{c}1\\ 2\\ 3\end{array}\right)$$
多行中括号	\left[ \begin{array}{c}1\2\3\\end{array} \right]	$$\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$
多行大括号	\left{ \begin{array}{c}1\2\3\\end{array} \right}	$$\left\{\begin{array}{c}1\\ 2\\ 3\end{array}\right\}$$

解读：
	 \begin{array}{c}，array指一个矩阵，c指一列

绝对值

名称	AxMath	渲染后
绝对值	\mid a \mid	$$\mid a\mid$$

微分与积分

名称	AxMath	渲染后
微分	\frac{\mathrm{d}y}{\mathrm{d}x}	$$\frac{\mathrm{d}y}{\mathrm{d}x}$$
积分	\int_b^a{f\left( x \right) \mathrm{d}x}	$${\int }_b^{a}f\left(x\right)\mathrm{d}x$$
f’(x)	f\prime\left( x \right)	$$f\prime \left(x\right)$$

解读：\mathrm{要变成正体的字母}
	int_积分区间开始^积分区间结束{被积内容}
	f\left( x \right)表示f(x),\left和\right表示左小括号和右小括号

求和与累乘

名称	AxMath	渲染后
求和	\sum_{n=1}^{\infty}{f\left( x \right)}	$$\sum _{n=1}^{\infty }f\left(x\right)$$
累乘	\prod_{n=1}^{\infty}{f\left( x \right)}	$$\prod _{n=1}^{\infty }f\left(x\right)$$

解读：
	\sum{开始求和}^{结束求和}{函数}
	\prod_{开始累乘}^{结束累乘}{函数}

极限

名称	AxMath	渲染后
求极限	\lim_{x \to 0}	$$\underset{x\to 0}{\lim }$$

解读：
	\lim_{x \to 0}x趋于0

计算时等号对齐

每个等号前面加上& 空格
& =公式

\begin{aligned} 这里开始
\text{原式}& =\lim_{n\rightarrow \infty} \left[ \sqrt{1+2+…+n}-\sqrt{1+2+…+\left( n-1 \right)} \right]
\
& =\lim_{n\rightarrow \infty} \left[ \sqrt{\frac{n\left( 1+n \right)}{2}}-\sqrt{\frac{\left( 1+n-1 \right) n}{2}} \right]
\
& =\lim_{n\rightarrow \infty} \left[ \sqrt{\frac{n\left( 1+n \right)}{2}}-\sqrt{\frac{n^2}{2}} \right]
\
& =\lim_{n\rightarrow \infty} \left[ \frac{\frac{n+n^2-n2}{2}}{\sqrt{\frac{n\left( 1+n \right)}{2}}+\sqrt{\frac{n^2}{2}}} \right]
\
& =\sqrt{2}\lim_{n\rightarrow \infty} \left[ \frac{1}{\sqrt{1+\frac{1}{n}}+\sqrt{1}} \right]
\
& =\frac{\sqrt{2}}{2}
\end{aligned} 这里结束

渲染后
$$\begin{array}{rl}\text{原式}& =\underset{n\to \infty }{\lim }\left[\sqrt{1+2+...+n}-\sqrt{1+2+...+\left(n-1\right)}\right]\\ & =\underset{n\to \infty }{\lim }\left[\sqrt{\frac{n\left(1+n\right)}{2}}-\sqrt{\frac{\left(1+n-1\right)n}{2}}\right]\\ & =\underset{n\to \infty }{\lim }\left[\sqrt{\frac{n\left(1+n\right)}{2}}-\sqrt{\frac{n^2}{2}}\right]\\ & =\underset{n\to \infty }{\lim }\left[\frac{\frac{n+n^2-n^2}{2}}{\sqrt{\frac{n\left(1+n\right)}{2}}+\sqrt{\frac{n^2}{2}}}\right]\\ & =\sqrt{2}\underset{n\to \infty }{\lim }\left[\frac{1}{\sqrt{1+\frac{1}{n}}+\sqrt{1}}\right]\\ & =\frac{\sqrt{2}}{2}\end{array}$$

希腊字母

名称	AxMath	渲染后
Alpha	\alpha	$$\alpha$$
Beta	\beta	$$\beta$$
Gamma	\gamma	$$\gamma$$
Delat	\delta	$$\delta$$

举个例子

a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos mx\mathrm{d}x}

$$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)\cos mx\mathrm{d}x$$