深度学习(吴恩达)知识总结
深度学习
logistic回归
y
^
=
σ
(
w
T
x
+
b
)
\hat{y}=\sigma(w^Tx+b)
y^=σ(wTx+b),where
σ
(
z
)
=
1
1
+
e
−
z
\sigma(z)=\frac{1}{1+e^{-z}}
σ(z)=1+e−z1
cost function:
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
y
^
,
y
(
i
)
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
o
g
y
^
(
i
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
y
^
(
i
)
)
]
J(w,b)=\frac{1}{m}\sum_{i=1}^{m}\mathscr{L}(\hat{y},y^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log\hat{y}^{(i)}+(1-y^{(i)})log(1-\hat{y}^{(i)})]
J(w,b)=m1∑i=1mL(y^,y(i))=−m1∑i=1m[y(i)logy^(i)+(1−y(i))log(1−y^(i))]
w
=
w
−
α
d
J
(
w
,
b
)
d
w
w=w-\alpha\frac{dJ(w,b)}{dw}
w=w−αdwdJ(w,b)
b
=
b
−
α
d
J
(
w
,
b
)
d
b
b=b-\alpha\frac{dJ(w,b)}{db}
b=b−αdbdJ(w,b)\
Python中的技巧
a=np.random.randn(5,1) # a.shape=(5, 1) 5行1列的矩阵
a=a.reshape(5,1) # 将a转换成5行1列的矩阵
神经网络
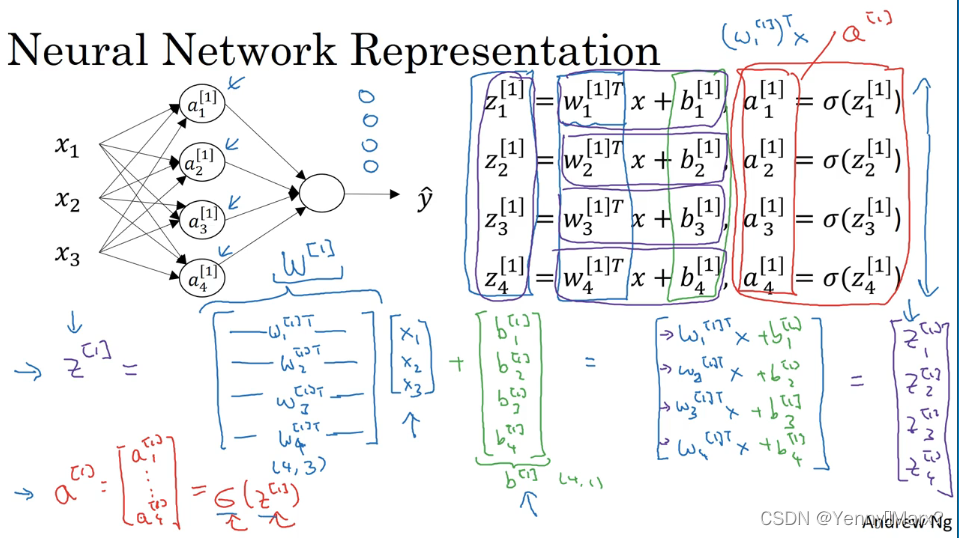
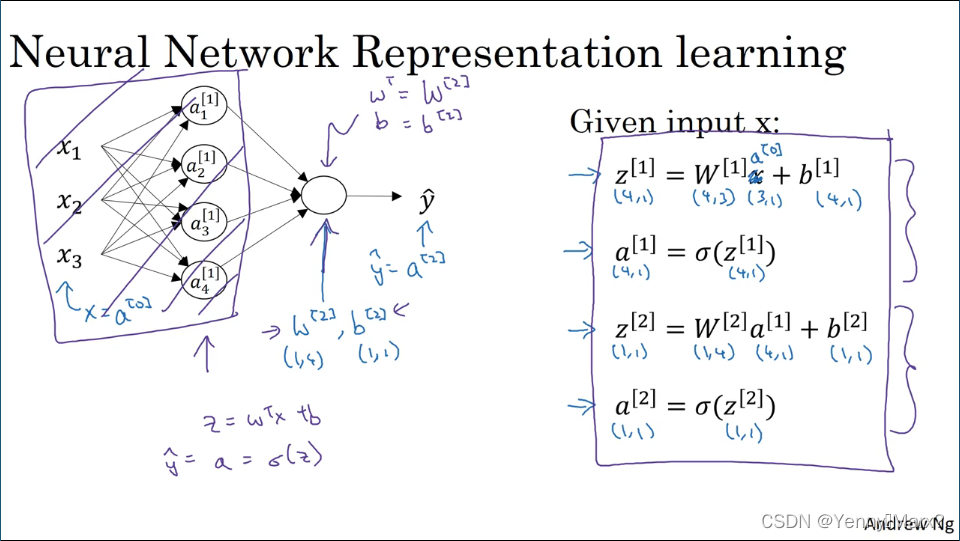
激活函数
| Activation function | Formula | Picture |
|---|---|---|
| sigmoid | a = 1 1 + e − z a=\frac{1}{1+e^{-z}} a=1+e−z1 | 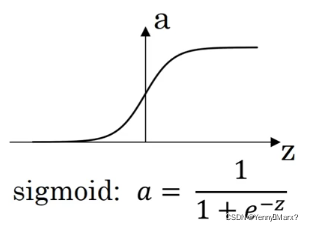 |
| tanh | a = e z − e − z e z + e − z a=\frac{e^z-e^{-z}}{e^z+e^{-z}} a=ez+e−zez−e−z | 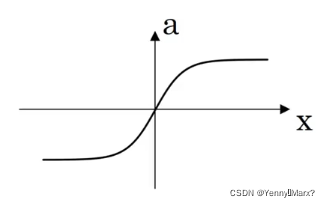 |
| ReLU | a = m a x ( 0 , z ) a=max(0,z) a=max(0,z) | 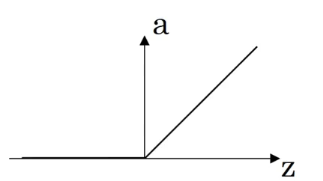 |
| Leaky ReLU | a = m a x ( 0.01 z , z ) a=max(0.01z,z) a=max(0.01z,z) | 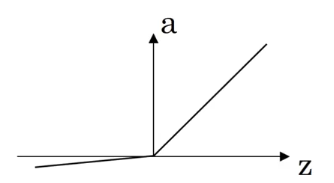 |
激活函数利弊:
| Activation function | Advantage | Disadvantage |
|---|---|---|
| sigmoid | 1. Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1,因此它对每个神经元的输出进行了归一化; 2.用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1,因此 Sigmoid 函数非常合适; 3. 梯度平滑,避免「跳跃」的输出值; 4. 函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率; 5. 明确的预测,即非常接近 1 或 0。 | 1. 梯度消失:注意:Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦,也就是说,Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时,输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此,这些神经元的权重不会更新。此外,与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此,想象一下,如果一个大型神经网络包含 Sigmoid 神经元,而其中很多个都处于饱和状态,那么该网络无法执行反向传播。 2. 不以零为中心:Sigmoid 输出不以零为中心的,,输出恒大于0,非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(Bias Shift),并进一步使得梯度下降的收敛速度变慢。 3. 计算成本高昂:exp() 函数与其他非线性激活函数相比,计算成本高昂,计算机运行起来速度较慢。 |
| Tanh | 1. 当输入较大或较小时,输出几乎是平滑的并且梯度较小,这不利于权重更新。二者的区别在于输出间隔,tanh 的输出间隔为 1,并且整个函数以 0 为中心,比 sigmoid 函数更好; 2. 在 tanh 图中,负输入将被强映射为负,而零输入被映射为接近零。 | 与sigmoid类似,Tanh 函数也会有梯度消失的问题,因此在饱和时(x很大或很小时)也会「杀死」梯度。 |
| ReLU | 1. 当输入为正时,导数为1,一定程度上改善了梯度消失问题,加速梯度下降的收敛速度; 2. 计算速度快得多。ReLU 函数中只存在线性关系,因此它的计算速度比 sigmoid 和 tanh 更快。 3 .被认为具有生物学合理性(Biological Plausibility),比如单侧抑制、宽兴奋边界(即兴奋程度可以非常高) | 1. Dead ReLU 问题。当输入为负时,ReLU 完全失效,在正向传播过程中,这不是问题。有些区域很敏感,有些则不敏感。但是在反向传播过程中,如果输入负数,则梯度将完全为零; 2.不以零为中心:和 Sigmoid 激活函数类似,ReLU 函数的输出不以零为中心,ReLU 函数的输出为 0 或正数,给后一层的神经网络引入偏置偏移,会影响梯度下降的效率。 |
| Leaky ReLU | 1. Leaky ReLU 通过把 x 的非常小的线性分量给予负输入(0.01x)来调整负值的零梯度(zero gradients)问题,当 x < 0 时,它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题。 2.Leak 有助于扩大 ReLU 函数的范围,通常 a 的值为 0.01 左右; 3. Leaky ReLU 的函数范围是(负无穷到正无穷) | |
| 为什么要使用非线性激活函数? | ||
| 计算量更少,只有一个地方需要使用线性激活函数:就是如果机器学习的是回归问题,可以在输出层使用线性激活函数。 |
权重初始化:
w
[
1
]
=
n
p
.
r
a
n
d
o
m
.
r
a
n
d
n
(
(
2
,
2
)
)
∗
0.01
w^{[1]}=np.random.randn((2,2))*0.01
w[1]=np.random.randn((2,2))∗0.01 #如果不是0.01而是100的话,容易在一开始z就很大,在两端平缓区域,导致tanh或sigmoid激活函数接近饱和,从而减慢学习速度。
b
[
1
]
=
n
p
.
z
e
r
o
(
(
2
,
1
)
)
b^{[1]}=np.zero((2,1))
b[1]=np.zero((2,1)) #2表示有两个特征,1表示有一个隐藏神经元(一组数据)
w
[
2
]
=
n
p
.
r
a
n
d
o
m
.
r
a
n
d
n
(
(
1
,
2
)
)
∗
0.01
w^{[2]}=np.random.randn((1,2))*0.01
w[2]=np.random.randn((1,2))∗0.01
b
[
2
]
=
0
b^{[2]}=0
b[2]=0
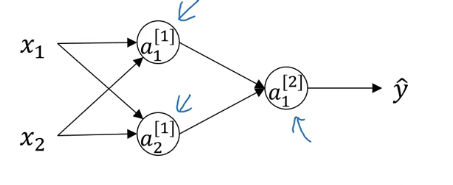
深层神经网络
前向传播:
输入:
a
[
l
−
1
]
a^{[l-1]}
a[l−1]
输出:
a
[
l
]
a^{[l]}
a[l],cache(
z
[
l
]
z^{[l]}
z[l])
z
[
l
]
=
w
[
l
]
∗
a
[
l
−
1
]
+
b
[
l
]
z^{[l]}=w^{[l]}*a^{[l-1]}+b^{[l]}
z[l]=w[l]∗a[l−1]+b[l]
a
[
l
]
=
g
[
l
]
(
z
[
l
]
)
a^{[l]}=g^{[l]}(z^{[l]})
a[l]=g[l](z[l])
反向传播:
输入:
d
a
[
l
]
da^{[l]}
da[l]
输出:
d
a
[
l
−
1
]
,
d
W
[
l
]
,
d
b
[
l
]
da^{[l-1]},dW^{[l]},db^{[l]}
da[l−1],dW[l],db[l]
d
z
[
l
]
=
d
a
[
l
]
∗
g
[
l
]
′
(
z
[
l
]
)
dz^{[l]}=da^{[l]}*g^{[l]^{'}}(z^{[l]})
dz[l]=da[l]∗g[l]′(z[l])
d
w
[
l
]
=
d
z
[
l
]
∗
a
[
l
−
1
]
dw^{[l]}=dz^{[l]}*a^{[l-1]}
dw[l]=dz[l]∗a[l−1]
d
b
[
l
]
=
d
z
[
l
]
db^{[l]}=dz^{[l]}
db[l]=dz[l]
d
a
[
l
−
1
]
=
w
[
l
]
T
∗
d
z
[
l
]
da^{[l-1]}=w^{[l]^T}*dz^{[l]}
da[l−1]=w[l]T∗dz[l]
d
z
[
l
]
=
w
[
l
+
1
]
T
∗
d
z
[
l
+
1
]
∗
g
[
l
]
′
(
z
[
l
]
)
dz^{[l]}=w^{[l+1]^T}*dz^{[l+1]}*g^{[l]^{'}}(z^{[l]})
dz[l]=w[l+1]T∗dz[l+1]∗g[l]′(z[l])
w维数:(当前层神经元个数,上一层神经元个数)=(
n
[
l
]
,
n
[
l
−
1
]
n^{[l]},n^{[l-1]}
n[l],n[l−1])
b维数:(当前层神经元个数,1)=(
n
[
l
]
,
1
n^{[l]},1
n[l],1)
dw维数:(当前层神经元个数,上一层神经元个数)=(
n
[
l
]
,
n
[
l
−
1
]
n^{[l]},n^{[l-1]}
n[l],n[l−1])
db维数:(当前层神经元个数,1)=(
n
[
l
]
,
1
n^{[l]},1
n[l],1)
z维数:(当前层神经元个数,1)=(
n
[
l
]
,
1
n^{[l]},1
n[l],1)
Z维数:(当前层神经元个数,m)=(
n
[
l
]
,
m
n^{[l]},m
n[l],m) m为训练样本个数
Dropout正则化:随机丢失部分神经元数据
神经网络权重的初始化:将
V
a
r
(
w
i
)
=
1
n
Var(w_i)=\frac{1}{n}
Var(wi)=n1
梯度的数值逼近
设
f
(
θ
)
=
θ
3
,
θ
=
1
f(\theta)=\theta^3,\theta=1
f(θ)=θ3,θ=1
单边误差:
g
(
θ
)
=
f
(
θ
+
ε
)
−
f
(
θ
)
ε
=
3.0301
g(\theta)=\frac{f(\theta+\varepsilon)-f(\theta)}{\varepsilon}=3.0301
g(θ)=εf(θ+ε)−f(θ)=3.0301,
e
r
r
o
r
=
0.0301
error=0.0301
error=0.0301
双边误差:
g
(
θ
)
≈
f
(
θ
+
ε
)
−
f
(
θ
−
ε
)
2
ε
=
3.0001
g(\theta)\approx\frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}=3.0001
g(θ)≈2εf(θ+ε)−f(θ−ε)=3.0001,
e
r
r
o
r
=
0.0001
error=0.0001
error=0.0001
g
(
θ
)
=
3
θ
2
=
3
g(\theta)=3\theta^2=3
g(θ)=3θ2=3
Mini-batch 梯度下降
梯度:梯度是代价函数对每个参数的偏导数。
不全部取所有的样本,只取一部分,分别计算拟合函数值,再计算代价函数,然后反向传播计算梯度,更新权重w。若有5万个样本,每次梯度下降的样本数量是100个,则要进行500次梯度下降。
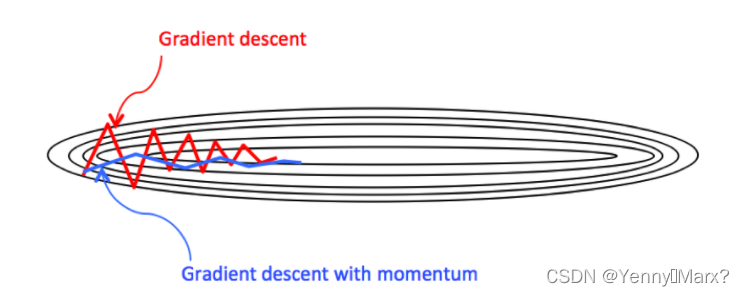
动量梯度下降
指数加权平均
v t = β v t − 1 + ( 1 − β ) θ t v_t=\beta v_{t-1}+(1-\beta)\theta _t vt=βvt−1+(1−β)θt # 与前面的时刻有关,且时间离的越远,影响越小
动量梯度下降公式
引入动量
v
d
w
=
β
v
d
w
+
(
1
−
β
)
d
w
v_{dw}=\beta v_{dw}+(1-\beta)dw
vdw=βvdw+(1−β)dw,
v
d
b
=
β
v
d
b
+
(
1
−
β
)
d
b
v_{db}=\beta v_{db}+(1-\beta)db
vdb=βvdb+(1−β)db,dw是横轴梯度,db是纵轴梯度,
β
\beta
β通常取0.9。
则
w
=
w
−
α
v
d
w
w=w-\alpha v_{dw}
w=w−αvdw,
b
=
b
−
α
v
d
b
b=b-\alpha v_{db}
b=b−αvdb,w为横轴方向,b为纵轴方向,目的是要减缓纵轴的震荡,加快横轴的收敛速度。
作用:使得梯度下降的方向由梯度方向和动量方向共同决定,减小梯度下降过程中的震荡。
RMSprop
s
d
w
=
β
s
d
w
+
(
1
−
β
)
d
w
2
s_{dw}=\beta s_{dw}+(1-\beta)dw^2
sdw=βsdw+(1−β)dw2
s
d
b
=
β
s
d
b
+
(
1
−
β
)
d
b
2
s_{db}=\beta s_{db}+(1-\beta)db^2
sdb=βsdb+(1−β)db2
w
=
w
−
α
d
w
s
d
w
w=w-\alpha \frac{dw}{\sqrt{s_{dw}}}
w=w−αsdwdw
b
=
b
−
α
d
b
s
d
b
b=b-\alpha \frac{db}{\sqrt{s_{db}}}
b=b−αsdbdb
Adam优化算法
v
d
w
=
β
1
v
d
w
+
(
1
−
β
1
)
d
w
v_{dw}=\beta _1 v_{dw}+(1-\beta _1)dw
vdw=β1vdw+(1−β1)dw
v
d
b
=
β
1
v
d
b
+
(
1
−
β
1
)
d
b
v_{db}=\beta _1v_{db}+(1-\beta _1)db
vdb=β1vdb+(1−β1)db
s
d
w
=
β
2
s
d
w
+
(
1
−
β
2
)
d
w
2
s_{dw}=\beta _2 s_{dw}+(1-\beta _2)dw^2
sdw=β2sdw+(1−β2)dw2
s
d
b
=
β
2
s
d
b
+
(
1
−
β
2
)
d
b
2
s_{db}=\beta _2s_{db}+(1-\beta _2)db^2
sdb=β2sdb+(1−β2)db2
v
d
w
c
o
r
r
e
c
t
e
d
=
v
d
w
1
−
β
1
t
v_{dw}^{corrected}=\frac{v_{dw}}{1-\beta _1^t}
vdwcorrected=1−β1tvdw,t为迭代次数
v
d
b
c
o
r
r
e
c
t
e
d
=
v
d
b
1
−
β
1
t
v_{db}^{corrected}=\frac{v_{db}}{1-\beta _1^t}
vdbcorrected=1−β1tvdb
s
d
w
c
o
r
r
e
c
t
e
d
=
s
d
w
1
−
β
2
t
s_{dw}^{corrected}=\frac{s_{dw}}{1-\beta _2^t}
sdwcorrected=1−β2tsdw
s
d
b
c
o
r
r
e
c
t
e
d
=
s
d
b
1
−
β
2
t
s_{db}^{corrected}=\frac{s_{db}}{1-\beta _2^t}
sdbcorrected=1−β2tsdb
w
=
w
−
α
v
d
w
c
o
r
r
e
c
t
e
d
s
d
w
+
ε
w=w-\alpha \frac{v_{dw}^{corrected}}{\sqrt{s_{dw}}+\varepsilon}
w=w−αsdw+εvdwcorrected
b
=
b
−
α
v
d
b
c
o
r
r
e
c
t
e
d
s
d
b
+
ε
b=b-\alpha \frac{v_{db}^{corrected}}{\sqrt{s_{db}}+\varepsilon}
b=b−αsdb+εvdbcorrected
学习率衰减
1 epoch=1 pass through data
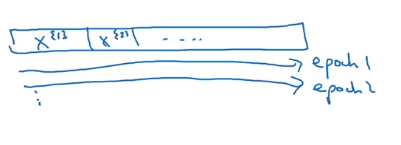
公式一:
α
=
1
1
+
d
e
c
a
y
r
a
t
e
∗
e
p
o
c
h
n
u
m
∗
α
0
\alpha=\frac{1}{1+decayrate*epochnum}*\alpha_0
α=1+decayrate∗epochnum1∗α0,
α
0
\alpha_0
α0为初始学习率。
公式二:
α
=
0.9
5
e
p
o
c
h
n
u
m
∗
α
0
\alpha=0.95^{epochnum}*\alpha_0
α=0.95epochnum∗α0
公式三:
α
=
k
e
p
o
c
h
n
u
m
∗
α
0
\alpha=\frac{k}{\sqrt {epochnum}}*\alpha_0
α=epochnumk∗α0,k为常数
公式四:
α
=
k
t
∗
α
0
\alpha=\frac{k}{\sqrt {t}}*\alpha_0
α=tk∗α0,t为mini-batch的样本数
调试处理
α
\alpha
α:学习率
β
\beta
β:momentum参数,一般为0.9
mini-batch:样本数
hidden inits:隐藏层单元
layers:层数
learning rate decay:学习率衰减
Adam算法
β
1
、
β
2
、
ε
\beta _1、\beta _2、\varepsilon
β1、β2、ε:一般设
0.9
、
0.999
、
1
0
−
8
0.9、0.999、10^{-8}
0.9、0.999、10−8
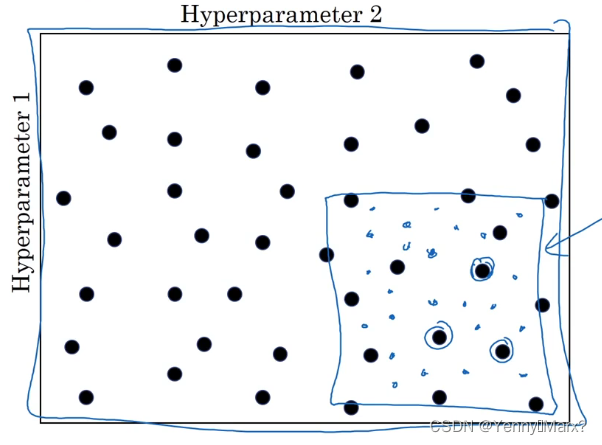
选取调试值方法:网格法、数标尺。
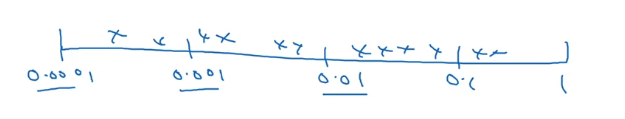
batch归一化
归一化:使数据的均值为0,方差为1,符合正态分布,通常在激活之前进行batch-normal。以下公式中,m为mini-batch的样本数。
作用:减少前层参数对后层的影响,加速整个网络的学习;有正则化的效果,给隐藏层添加了噪音。
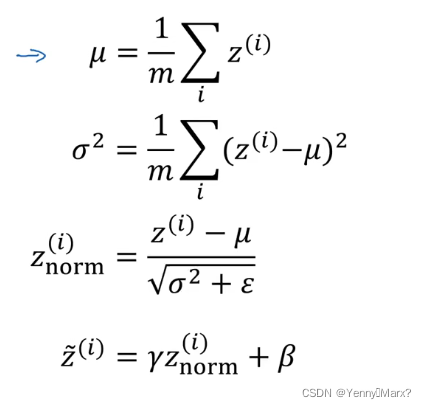


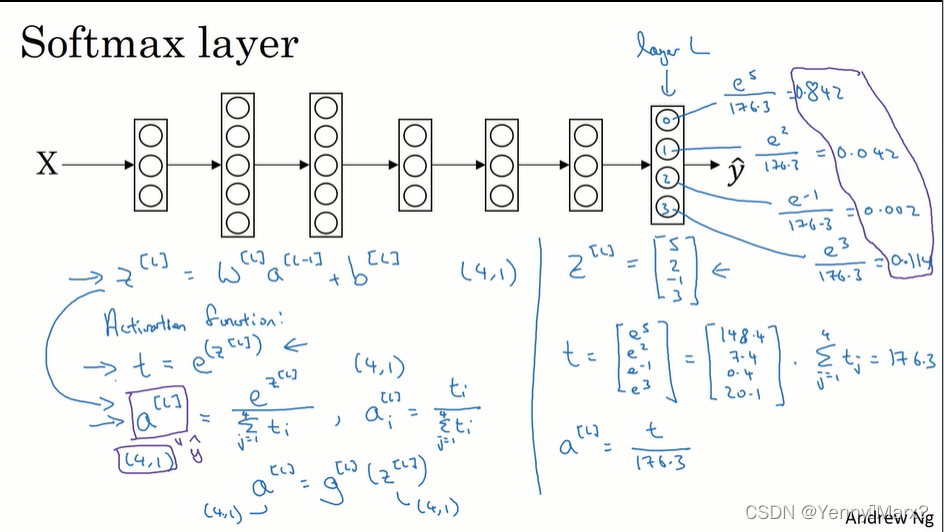
Softmax激活函数分类


Tensorflow
函数训练
w=tf.Variable(0,dtype=tf.float32) #初始化参数
cost=tf.add(tf.add(w**2,tf.multiply(-10.,w)),25)
train=tf.train.GradientDescentOptimizer(0.01).minimize(cost) #学习率0.01,目标是最小化损失
init=tf.global_variables_initializer()
session=tf.Session()
session.run(init) #初始化全局变量
session.run(train) #运行一步梯度下降法
for i in range(1000): #运行下降1000次迭代
session.run(train)
训练集训练
import numpy as np
import tensorflow as tf
coefficients=np.array([[1.],[-20.],[25.]])
x=tf.placeholder(tf.float32,[3,1]) #x为3行一列的训练数据
cost=tf.add(tf.add(w2,tf.multiply(-10.,w)),25)
cost=x[0][0]*w2+x[1][0]*w+x[2][0]
train=tf.train.GradientDescentOptimizer(0.01).minimize(cost) #学习率0.01,目标是最小化损失
init=tf.global_variables_initializer()
session=tf.Session()
session.run(train,feed+dict={x:coefficients}) #运行一步梯度下降法
卷积神经网络
padding
图像大小:n×n,滤波核大小f×f,则输出维度是
(
n
−
f
+
1
)
×
(
n
−
f
+
1
)
(n-f+1)×(n-f+1)
(n−f+1)×(n−f+1)
填充的目的:充分利用边缘特征值,发挥角落或图像边缘的信息作用。输出变成
(
n
+
2
p
−
f
+
1
)
×
(
n
+
2
p
−
f
+
1
)
(n+2p-f+1)×(n+2p-f+1)
(n+2p−f+1)×(n+2p−f+1),p=padding=1,p表示添加了几圈。
Valid卷积——没有padding
Same卷积——填充后,输入和输出的尺寸没有变,即n+2p-f+1=n,
p
=
f
−
1
2
p=\frac{f-1}{2}
p=2f−1,当卷积核边长是奇数时,输入和输出尺寸一样大,因此一般采用的卷积核长度为奇数。
卷积步长
图像大小:n×n,滤波核大小f×f,padding:p,stride=s,则输出尺寸为: i n t ( n + 2 p − f s + 1 ) × i n t ( n + 2 p − f s + 1 ) int(\frac{n+2p-f}{s}+1)×int(\frac{n+2p-f}{s}+1) int(sn+2p−f+1)×int(sn+2p−f+1),int表示向下取整
三维卷积(可用于RGB图像)
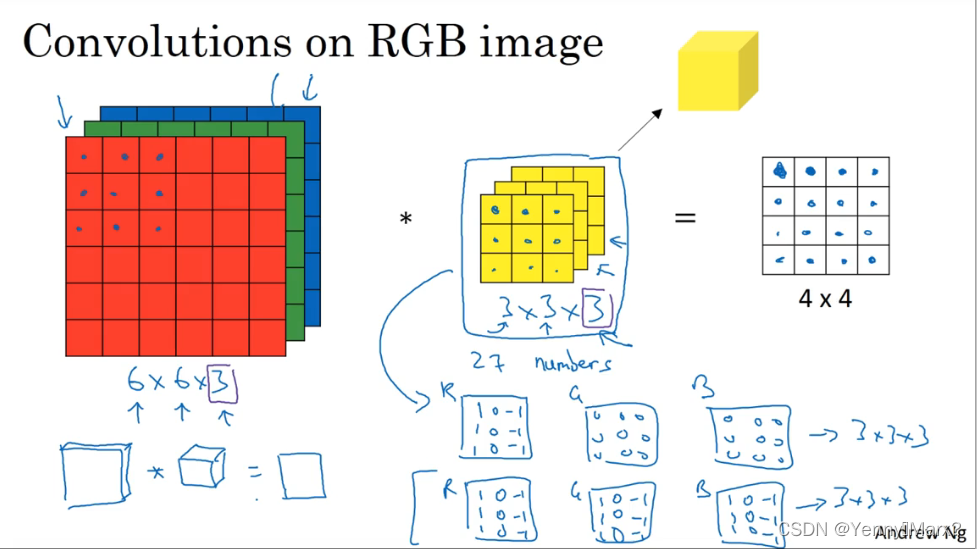
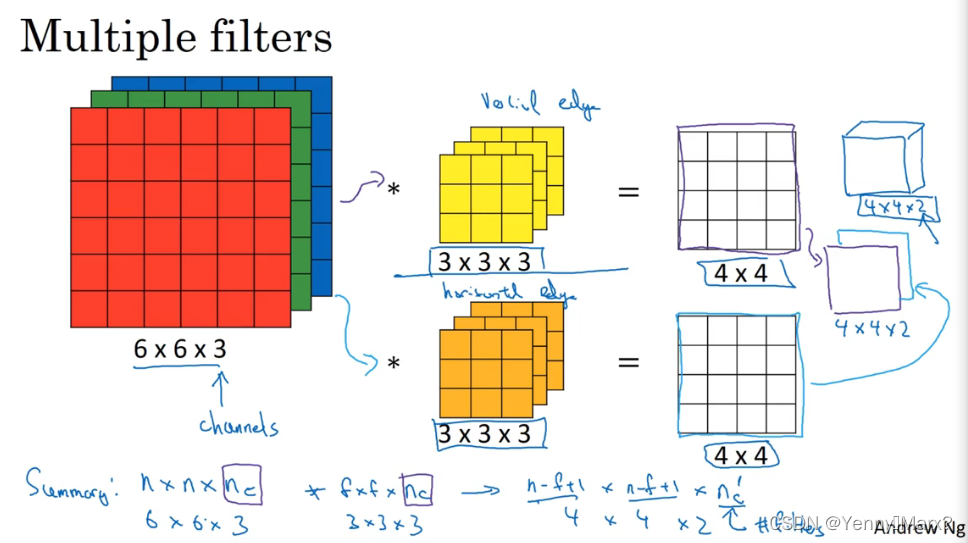
多核卷积(垂直、水平)
图像:
n
×
n
×
n
c
n×n×n_c
n×n×nc,卷积核
f
×
f
×
n
c
f×f×n_c
f×f×nc,
n
c
n_c
nc为通道数,则输出图像尺寸为:
(
n
−
f
+
1
)
×
(
n
−
f
+
1
)
×
n
c
′
(n-f+1)×(n-f+1)×n_c^{'}
(n−f+1)×(n−f+1)×nc′,
n
c
′
n_c^{'}
nc′为使用的滤波器的个数
单层卷积神经网络
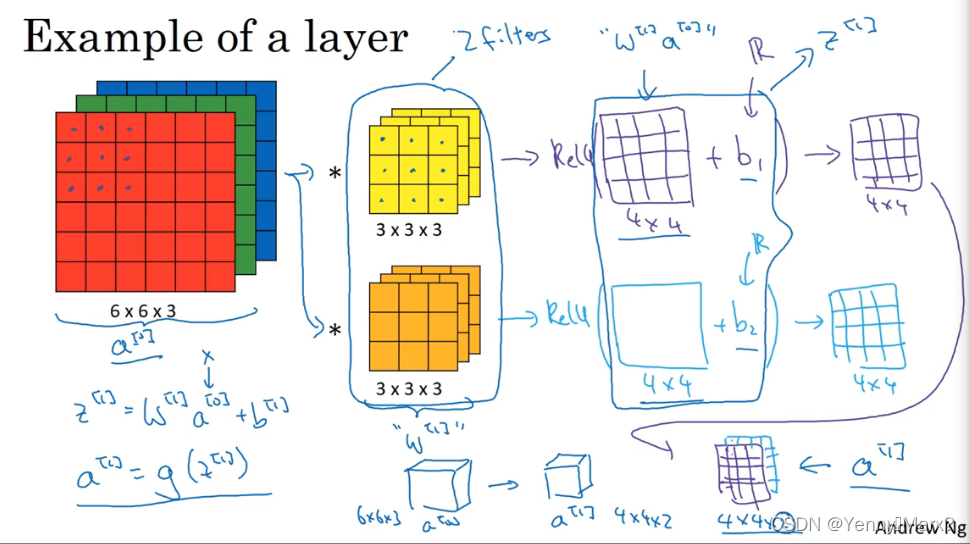
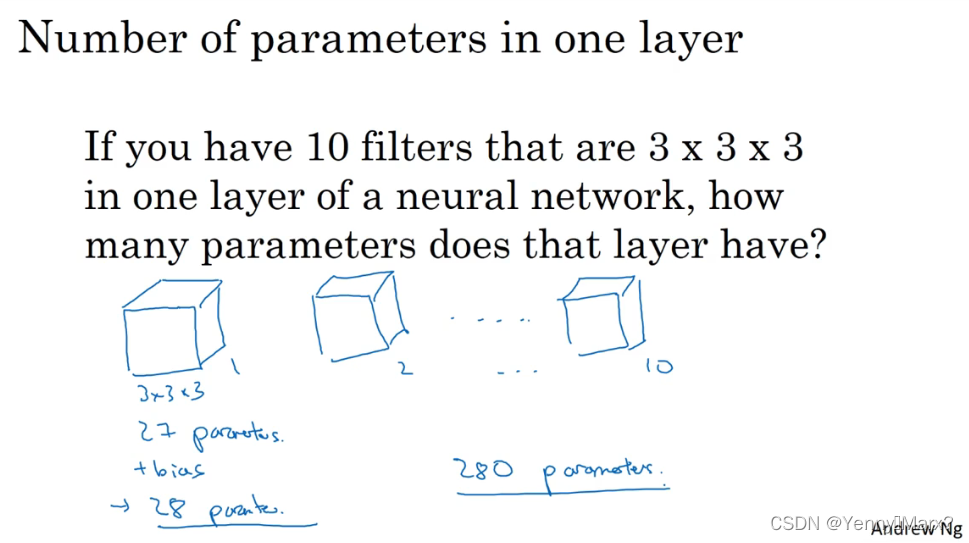
参数的个数与滤波器的个数和大小有关,与图像的尺寸无关。

池化层
Max-pooling(常用):选取区域内的最大值。
最大池化输出大小:
i
n
t
(
n
+
2
p
−
f
s
+
1
)
×
i
n
t
(
n
+
2
p
−
f
s
+
1
)
int(\frac{n+2p-f}{s}+1)×int(\frac{n+2p-f}{s}+1)
int(sn+2p−f+1)×int(sn+2p−f+1),常用值:
f
=
2
,
s
t
r
i
d
e
=
2
,
p
=
0
f=2,stride=2,p=0
f=2,stride=2,p=0,相互于高度和宽度减半。
平均池化:选取区域内的平均值。
注意!池化层没有要学习的参数。
图像增强
- 垂直镜像对称
- 色彩转换
非极大值抑制
1.丢弃概率小于或等于预定阈值(例如0.5)的所有方框;
2.对于剩余的边界框:选择具有最高概率的边界框并将其作为输出预测;
3.计算相关联的边界框的IoU值(交并比),舍去IoU大于阈值的边界框;
4.重复步骤2,直到所有边界框都被视为输出预测或被舍弃;
Yolo算法步骤
1.输入一个图像,先将其分成n×n的网格。
2.对每个网格应用CNN模型进行图像分类和定位处理,获得预测对象的边界框及其对应的类概率。
3.非极大值抑制得到最终目标结果。