二叉树的基本操作-C语言实现-数据结构作业
目录
(5)将二叉树所有节点的左右子树互换(左子树变右子树,右子树变左子树);
编写一个带菜单的实验演示系统(参考前面实验的菜单系统)。要求演示以下功能(界面、函数及相关数据结构等根据需要自行设计和定义):
(1)二叉树的创建;
(2)二叉树的先序、中序和后序遍历输出;
(3)输出二叉树的叶子节点和度为2的节点的数量;
(4)输出二叉树的深度;
(5)将二叉树所有节点的左右子树互换(左子树变右子树,右子树变左子树);
(6)参考书上,二叉树按层次输出(一行输出一层);
(7)删除二叉树(释放二叉树所有节点空间);

(1)二叉树的创建;
BiTree CreatePreTree()//建立二叉树
{
char c;
scanf("%c", &c);
if (c == '#') //表示空子树
return NULL;
else
{
BiTree T = (BiTree)malloc(sizeof(BiTreeNode));
T->data = c;
T->leftChild = CreatePreTree();
T->rightChild = CreatePreTree();
return T;
}
}(2)二叉树的先序、中序和后序遍历输出;
void PreOrder(BiTreeNode* root, void visit(DataType item)) {
//前序遍历二叉树root,访问操作为visit
if (root != NULL)
{
visit(root->data);
PreOrder(root->leftChild, visit);
PreOrder(root->rightChild, visit);
}
}
void InOrder(BiTreeNode* root, void visit(DataType item)) {
//中序遍历二叉树root,访问操作为visit
if (root != NULL)
{
InOrder(root->leftChild, visit);
visit(root->data);
InOrder(root->rightChild, visit);
}
}
void PostOrder(BiTreeNode* root, void visit(DataType item)) {
//后序遍历二叉树root,访问操作为visit
if (root != NULL)
{
PostOrder(root->leftChild, visit);
PostOrder(root->rightChild, visit);
visit(root->data);
}
}
(3)输出二叉树的叶子节点和度为2的节点的数量;
int Count1(BiTree bt)//计算叶子结点个数
{
if (bt == NULL) return 0;
else if (bt->leftChild == NULL && bt->rightChild == NULL)
return 1;
else
return (Count1(bt->leftChild) + Count1(bt->rightChild));
}
int Count2(BiTree bt)//计算度为2的节点的数量
{
int num = 0;
if (bt)
{
if (bt->leftChild != NULL && bt->rightChild != NULL)
{
num = 1;
}
num += Count2(bt->leftChild) + Count2(bt->rightChild);
}
return num;
}(4)输出二叉树的深度;
如果二叉树只有根节点,那么它的高度就为1。否则二叉树的高度等于1+左、右子树高度的较大者。按这种方法递归实现。
int Treehigh(BiTree bt)
{
int lefthigh, righthigh, high;
if (bt == NULL) high = 0;//空树
else
{
lefthigh = Treehigh(bt->leftChild);
righthigh = Treehigh(bt->rightChild);
int i = lefthigh > righthigh ? lefthigh : righthigh;//找到子树的深度
high = i + 1;//子树深度+1=树的深度
}
return high;
}(5)将二叉树所有节点的左右子树互换(左子树变右子树,右子树变左子树);

void ChangeTree(BiTree bt)
{
BiTree temp = (BiTree)malloc(sizeof(BiTreeNode));
if (bt)
{
temp = bt->rightChild;
bt->rightChild = bt->leftChild;
bt->leftChild = temp;//上面三步,把bt结点的左右结点交换成功
ChangeTree(bt->leftChild);
ChangeTree(bt->rightChild);
}
else return;
}(6)参考书上,二叉树按层次输出(一行输出一层);
Queue InitQueue()
{ //初始化队列
Queue seq;
for (int i = 0; i < QueueMax; i++)
{
seq.data[i] = NULL;
}
seq.head = 0;
seq.rear = -1;
seq.len = 0;
return seq;
}
int IsEmptyQueue(Queue seq)
{ //队列判空
if (seq.len == 0) return 1;
return 0;
}
int IsFullQueue(Queue seq)
{ //队列判满
if (seq.len == QueueMax) return 1;
return 0;
}
void PushQueue(Queue* seq, BiTree T)
{ //入队
if (IsFullQueue(*seq)) {
printf("队列已满\n");
return;
}
seq->rear = (seq->rear + 1) % QueueMax;
seq->len++;
seq->data[seq->rear] = T;
}
void PopQueue(Queue* seq, BiTree* T)
{ //出队
if (IsEmptyQueue(*seq)) {
printf("队列已空\n");
return;
}
seq->head = (seq->head + 1) % QueueMax;
*T = seq->data[seq->head];
seq->len--;
}
void LevelOrder(BiTree T)
{ //层序遍历
Queue seq = InitQueue();
BiTree tmp = T;
PushQueue(&seq, tmp);
while (!IsEmptyQueue(seq))
{
printf("%c ", tmp->data);
if (tmp->leftChild != NULL)
{
PushQueue(&seq, tmp->leftChild);
}
if (tmp->rightChild != NULL)
{
PushQueue(&seq, tmp->rightChild);
}
PopQueue(&seq, &tmp);
}
}(7)删除二叉树(释放二叉树所有节点空间);
先删除左子树,再删除右子树,最后删除根节点,采用递归实现。
void Destory(BiTree T) //后序遍历,释放结点空间
{
if (T != NULL)
{
if (T->leftChild != NULL) Destory(T->leftChild);
if (T->rightChild != NULL) Destory(T->rightChild);
free(T);
}
}完整代码
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
#define QueueMax 100
typedef char DataType;
typedef struct Node {
//定义二叉树结点
DataType data;
struct Node* leftChild;
struct Node* rightChild;
}BiTreeNode, * BiTree;
typedef struct
{//定义队列
BiTree data[QueueMax];
int head;
int rear;
int len;
}Queue;
//输 入:ABDGL###H###CEIM###JN##O##F#K#P##
BiTree CreatePreTree(); //建立二叉树
int Count1(BiTree bt);//二叉树的叶子节点的数量
int Count2(BiTree bt);//度为2的节点的数量
int Treehigh(BiTree bt);//二叉树的深度
void ChangeTree(BiTree bt);//交换左右子树
Queue InitQueue(); //初始化队列
int IsEmptyQueue(Queue seq); //队列判空
int IsFullQueue(Queue seq); //队列判满
void PushQueue(Queue* seq, BiTree T); //入队
void PopQueue(Queue* seq, BiTree* T); //出队
void LevelOrder(BiTree T); //层序遍历
void PreOrder(BiTreeNode* root, void visit(DataType item));//前序遍历
void InOrder(BiTreeNode* root, void visit(DataType item));//中序遍历
void PostOrder(BiTreeNode* root, void visit(DataType item));//后序遍历
void visit(DataType item);//访问函数
void Destory(BiTree bt); //释放空间
int main()
{
BiTree T;
char sel = ' ';
while (sel != '0')
{
printf("------二叉树演示系统-------\n");
printf(" 版本:1.0 作者:XXX 日期:2022-05-07\n");
printf("------------------------------------------\n");
printf(" 1.创建二叉树\n");
printf(" 2.先序排列操作\n");
printf(" 3.中序排列操作\n");
printf(" 4.后序排列操作\n");
printf(" 5.输出二叉树的叶子节点和度为2的节点的数量\n");
printf(" 6.输出二叉树的深度\n");
printf(" 7.将二叉树所有节点的左右子树互换\n");
printf(" 8.层序排列操作\n");
printf(" 9.删除二叉树\n");
printf(" 0.退出系统\n");
printf("请输入选项[0-9]:");
sel = _getch();
switch (sel)
{
case '1':
printf("创建二叉树.\n");
T = CreatePreTree();
system("pause");
break;
case '2':
printf("先序排列操作.\n");
printf("前序遍历:");
PreOrder(T, visit);//前序遍历
system("pause");
break;
case '3':
printf("中序排列操作.\n");
printf("\n中序遍历:");
InOrder(T, visit);//中序遍历
system("pause");
break;
case '4':
printf("后序排列操作.\n");
printf("\n后序遍历:");
PostOrder(T, visit);//后序遍历
system("pause");
break;
case '5':
printf("输出二叉树的叶子节点和度为2的节点的数量.\n");
printf("叶子节点:%d个 \n", Count1(T));
printf("度为2的节点:%d个\n", Count2(T));
system("pause");
break;
case '6':
printf("输出二叉树的深度.\n");
printf("二叉树的深度为:%d\n", Treehigh(T));
system("pause");
break;
case '7':
printf("将二叉树所有节点的左右子树互换.\n");
ChangeTree(T);
system("pause");
break;
case '8':
printf("层序排列操作.\n");
printf("\n层序遍历:\n");
LevelOrder(T);//层序遍历
system("pause");
break;
case '9':
printf("删除二叉树.\n");
Destory(T);
printf("删除成功\n");
system("pause");
break;
case '0':
printf("\n谢谢使用,再见!\n");
break;
default:
printf("您输入的选项不合法,请重新选择!\n");
}
}
return 0;
}
void visit(DataType item)
{
printf("%c ", item);
}
BiTree CreatePreTree()//建立二叉树
{
char c;
scanf("%c", &c);
if (c == '#') //空格
return NULL;
else
{
BiTree T = (BiTree)malloc(sizeof(BiTreeNode));
T->data = c;
T->leftChild = CreatePreTree();
T->rightChild = CreatePreTree();
return T;
}
}
void PreOrder(BiTreeNode* root, void visit(DataType item)) {
//前序遍历二叉树root,访问操作为visit
if (root != NULL)
{
visit(root->data);
PreOrder(root->leftChild, visit);
PreOrder(root->rightChild, visit);
}
}
void InOrder(BiTreeNode* root, void visit(DataType item)) {
//中序遍历二叉树root,访问操作为visit
if (root != NULL)
{
InOrder(root->leftChild, visit);
visit(root->data);
InOrder(root->rightChild, visit);
}
}
void PostOrder(BiTreeNode* root, void visit(DataType item)) {
//后序遍历二叉树root,访问操作为visit
if (root != NULL)
{
PostOrder(root->leftChild, visit);
PostOrder(root->rightChild, visit);
visit(root->data);
}
}
Queue InitQueue()
{ //初始化队列
Queue seq;
for (int i = 0; i < QueueMax; i++)
{
seq.data[i] = NULL;
}
seq.head = 0;
seq.rear = -1;
seq.len = 0;
return seq;
}
int IsEmptyQueue(Queue seq)
{ //队列判空
if (seq.len == 0) return 1;
return 0;
}
int IsFullQueue(Queue seq)
{ //队列判满
if (seq.len == QueueMax) return 1;
return 0;
}
void PushQueue(Queue* seq, BiTree T)
{ //入队
if (IsFullQueue(*seq)) {
printf("队列已满\n");
return;
}
seq->rear = (seq->rear + 1) % QueueMax;
seq->len++;
seq->data[seq->rear] = T;
}
void PopQueue(Queue* seq, BiTree* T)
{ //出队
if (IsEmptyQueue(*seq)) {
printf("队列已空\n");
return;
}
seq->head = (seq->head + 1) % QueueMax;
*T = seq->data[seq->head];
seq->len--;
}
void LevelOrder(BiTree T)
{ //层序遍历
if (T == NULL) return;
BiTree tmp = T;
Queue seq = InitQueue();
int curlevel = 1;
int nextlevel = 0;
PushQueue(&seq, tmp);
while (!IsEmptyQueue(seq))//队列不空
{
printf("%c ", tmp->data);
curlevel--;
if (tmp->leftChild != NULL)
{
PushQueue(&seq, tmp->leftChild);
nextlevel++;
}
if (tmp->rightChild != NULL)
{
PushQueue(&seq, tmp->rightChild);
nextlevel++;
}
if (curlevel == 0)
{
printf("\n");
curlevel = nextlevel;
nextlevel = 0;
}
PopQueue(&seq, &tmp);
}
}
int Count1(BiTree bt)
{
if (bt == NULL) return 0;
else if (bt->leftChild == NULL && bt->rightChild == NULL)
return 1;
else
return (Count1(bt->leftChild) + Count1(bt->rightChild));
}
int Count2(BiTree bt)
{
int num = 0;
if (bt)
{
if (bt->leftChild != NULL && bt->rightChild != NULL)
{
num = 1;
}
num += Count2(bt->leftChild) + Count2(bt->rightChild);
}
return num;
}
int Treehigh(BiTree bt)
{
int lefthigh, righthigh, high;
if (bt == NULL) high = 0;//空树
else
{
lefthigh = Treehigh(bt->leftChild);
righthigh = Treehigh(bt->rightChild);
int i = lefthigh > righthigh ? lefthigh : righthigh;//找到子树的深度
high = i + 1;//子树深度+1=树的深度
}
return high;
}
void ChangeTree(BiTree bt)
{
BiTree temp = (BiTree)malloc(sizeof(BiTreeNode));
if (bt)
{
temp = bt->rightChild;
bt->rightChild = bt->leftChild;
bt->leftChild = temp;//上面三步,把bt结点的左右结点交换成功
ChangeTree(bt->leftChild);
ChangeTree(bt->rightChild);
}
else return;
}
void Destory(BiTree T) //后序遍历,释放结点空间
{
if (T != NULL)
{
if (T->leftChild != NULL) Destory(T->leftChild);
if (T->rightChild != NULL) Destory(T->rightChild);
free(T);
}
}运行结果展示

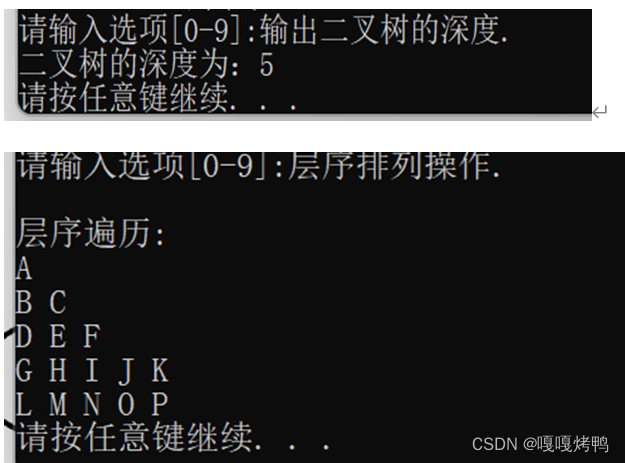
以上就是关于二叉树所有的解析啦。如果对你有帮助,记得点赞👍收藏 关注哦!
我的主页还有其他文章,欢迎学习指点。
关注我,让我们一起学习,一起成长吧!