机器人抓取系列——路径规划(RRT原理)
前面所述的点云分割+姿态估计能完成机器人抓取工作,但是如果抓取环境特比复杂,固定的抓取路径中有很多障碍物,那么就需要一种路径规划方法来规划出一条无碰撞的路线。
目前应用在机械臂上的路径规划算法主要分为人工势场法以及RRT(随机生成树)的方法,这里我用的是RRT的方法,因此主要介绍RRT方法的原理
RRT
RRT算法不仅可以在二维平面上适用,也适用于三维空间。今天主要记录一下二维的RRT算法原理,三维的RRT算法原理类似,只是增加一个维度即可。
RRT是一种通用的方法,不管什么机器人类型、不管自由度是多少、不管约束有多复杂都能用。而且它的原理很简单,这是它在机器人领域流行的主要原因之一。不过它的缺点也很明显,它得到的路径一般质量都不是很好,例如可能包含棱角,不够光滑,通常也远离最优路径。
那么下面就先介绍一下RRT的原理,然后再说一下路径不够光滑,以及远离最优距离是怎么解决的。
 与其他方法相比较,RRT有什么优势呢?
与其他方法相比较,RRT有什么优势呢?
其中一个很重要的优势就是快。RRT 的思想是快速扩张一群像树一样的路径以探索(填充)空间的大部分区域,伺机找到可行的路径。之所以选择“树”是因为它能够探索空间。在搜索轨迹的时候我们不知道出路应该在哪里,如果不在“确定”的搜索方向上,我们怎么找也找不到(找到的概率是0)。这时“随机”的好 处就体现出来了,虽然不知道出路在哪里,但是通过随机的反复试探还是能碰对的,而且碰对的概率随着试探次数的增多越来越大,就像买彩票一样,买的数量越多中奖的概率越大(RRT名字中“随机”的意思)。可是随机试探也讲究策略,如果我们从树中随机取一个点,然后向着随机的方向生长,那么结果是什么样的呢?见上图。可以看到,同样是随机树,但是这棵树并没很好地探索空间,它一直在起点(红点)附近打转。这可不好,我们希望树尽量经济地、均匀地探索空间,不要过度探索一个地方,更不能漏掉大部分地方。这样的一棵树怎么构造呢?
RRT的基本步骤是:
1、初始化整个空间,定义起始点,终点,采样点数,点与点之间的步长等信息
2、在空间中随机生成一个点Xrand
3、在已知树的点的集合中找到距离这个随机点最近的点Xnear
4、在Xnear到Xrand的直线方向上从Xnear以步长 t 截取点Xnew
5、判读Xnear和Xnew之间有没有障碍物,若存在障碍物则舍弃掉该点
6、将Xnew加入到树的集合中
7、循环2-6,循环截至的条件:有一个new点在终点的设定邻域内
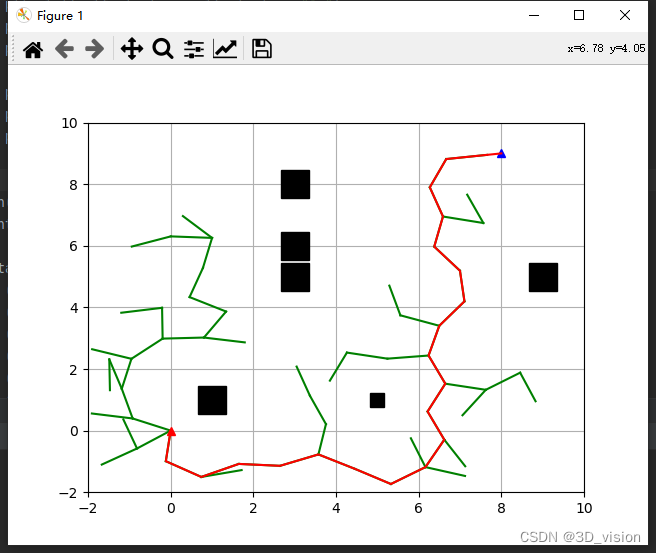
虽然这种方法能够找到有效的路径,但是同样也有一些问题
1、路径不够平滑
2、不是最优路径
RRT*
RRT*算法是相对于RRT算法的一个改进,相对于RRT来说,RRT *多了两个步骤:
1、重新为Xnew选择父节点
2、重布线随机树的过程
首先介绍RRT*重新选择父节点的过程
重新选择父节点过程
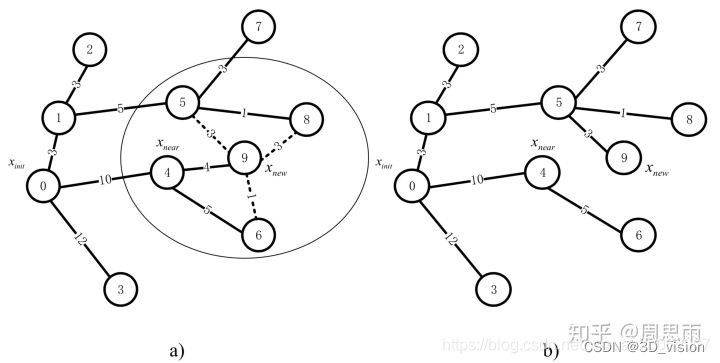
这里贴一张图,图中9节点是新产生的节点Xnew,6节点是产生9节点的父节点,,图中节点和节点之间的数值代表的是两点之间的欧氏距离。
在重新找父节点的过程中,以9节点 Xnew为圆心,以事先规定好的半径,找到在这个圆的范围内 Xnew 的近邻,也就是4,5,8节点(6节点是9的父节点)。
原来的路径0-4-6-9的代价为10+5+1=16
备选的三个节点 4,5,8和Xnew9节点组成的路径0 - 1 - 5 - 9,0 - 4 - 9和0 - 1 - 5 - 8 - 9代价分别为3 + 5 + 3 = 11,10 + 4 = 14和3 + 5 + 1 + 3 = 12,因此如果5节点作为9节点的新父节点,则路径代价相对是最小的,因此我们把9节点的父节点由原来的节点6变为节点5,则重新生成的随机树如图 b)所示。
重布线随机树过程
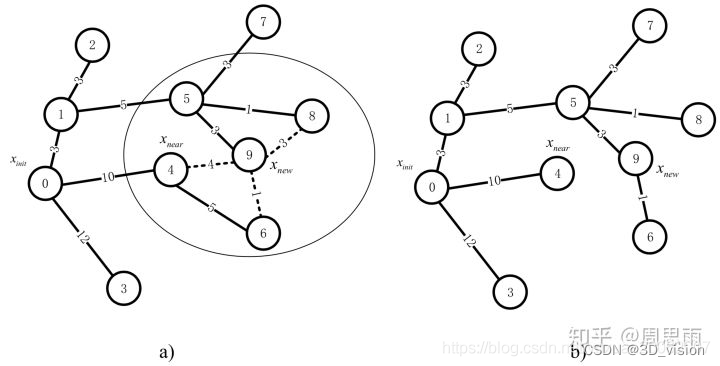
在为Xnew节点9重新选择父节点之后,为进一步使得随机树节点间连接的代价尽量小,为随机树进行重新布线。过程示意如上图所示,重布线的过程也可以被表述成:如果近邻节点的父节点改为 Xnew 可以减小路径代价,则进行更改。
比如上图,6节点一开始的路径代价为10+5=15,但是如果将他的父节点改成9,则他的路径代价则为3+5+3+1=12,因此更新6节点的父节点。
同理再看节点4和8,如果改变4和8的父节点变为9,那么他们的路径代价会变大,因此不改变4和8的父节点。
重布线过程的意义在于每当生成了新的节点后,是否可以通过重新布线,使得某些节点的路径代价减少。如果以整体的眼光看,并不是每一个重新布线的节点都会出现在最终生成的路径中,但在生成随机树的过程中,每一次的重布线都尽可能的为最终路径代价减小创造机会。
那么根据上述的RRT*的 重新选择父节点 和 重布线随机树过程 的过程,可以总结一下,RRT *相比于RRT来讲,他多了上述两个步骤:
重新选择父节点,就是以Xnew为中心画一个圈,假设在这个邻域中的点是Xnew的父节点,计算相应的路径代价,找到路径代价最小的那个父节点,然后对树进行一个更新。
重布线随机树过程:就是对Xnew的近邻点改变其父节点,让Xnew邻域内的节点的父节点都变成Xnew,因为这个时候Xnew的路径代价已经是最小的了,所以让Xnew邻域内的节点的父节点都变成Xnew,看是否能够减小各个节点的路径代价,如果路径代价减小了,则更新树。
RRT*算法的核心在于上述的两个过程:重新选择父节点和重布线。这两个过程相辅相成,重新选择父节点使新生成的节点路径代价尽可能小,重布线使得生成新节点后的随机树减少冗余通路,减小路径代价。
这里贴一个RRT* 的伪代码:(直接从别人那里截图过来的)


相对于RRT来讲,RRT*显然进行了一定程度的路径优化,但是这还不够,因此后续再介绍两种优化方式
双向RRT*
顾名思义就是从起始点和终点同时扩展树,直到两个树伸展到接近一定距离,然后直接进行拼接,这样减少了路径规划所消耗的时间。
贝塞尔曲线
这里先贴一个我用到的三阶贝塞尔曲线的python代码:
https://www.jb51.net/article/177375.htm
那么前面是对路径规划的路径距离的一个优化,但是生成的路径还是不平滑,因此利用研一所学的课程知识:贝塞尔曲线对规划的路径进行平滑处理:
三阶贝塞尔曲线的公式为:
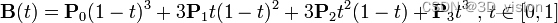
原理描述:
首先介绍一下一阶贝塞尔曲线:
一阶贝塞尔曲线需要2个控制点,假设分别为 P0 , P1。则贝塞尔曲线上的生成点p1(t)可以表达为:
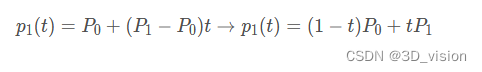
t的取值范围为[0,1],下面不再重复说明。
一阶曲线很好理解, 就是根据 t 来的线性插值。
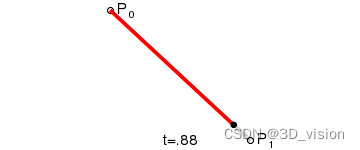
二阶贝塞尔曲线:
二阶贝塞尔曲线有三个控制点,分别为P0,P1, P2。其中P0和P1构成一阶,P1和P2也构成一阶,即:
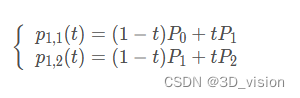
在生成两个一阶点的基础上,可以生成二阶贝塞尔点:
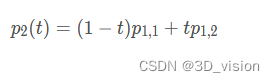
因此贝塞尔点与3个控制点的关系为:
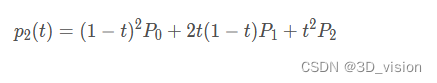
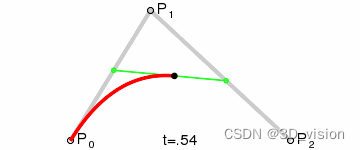
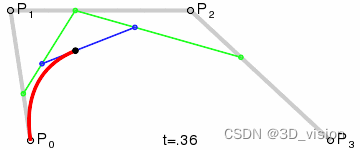
三阶贝塞尔曲线:
三阶贝塞尔曲线有4个控制点,假设分别为 P 0 , P 1 , P 2 , P 3 ,P0和P1,P1和P2、P2和P3 都构成一阶,即:
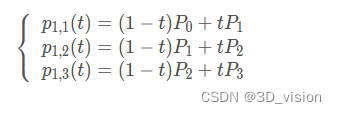
在生成的三个一阶点基础上,可以生成两个二 阶贝塞尔点:
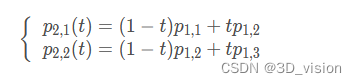
在生成的两个二阶点基础上,可以生成三阶贝 塞尔点:
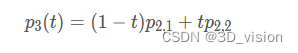
整理可得:
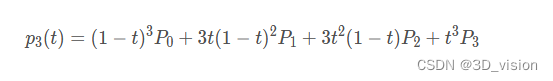
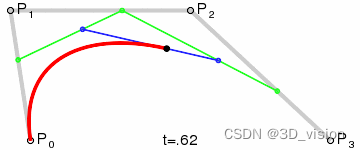
将贝塞尔曲线应用到RRT中
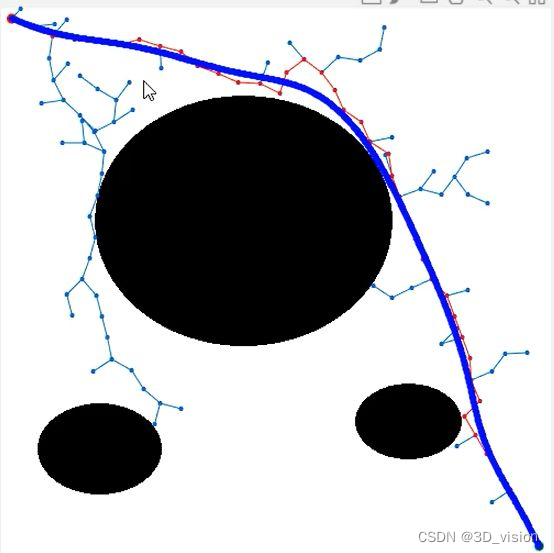
可以看出路径规划比较平滑。
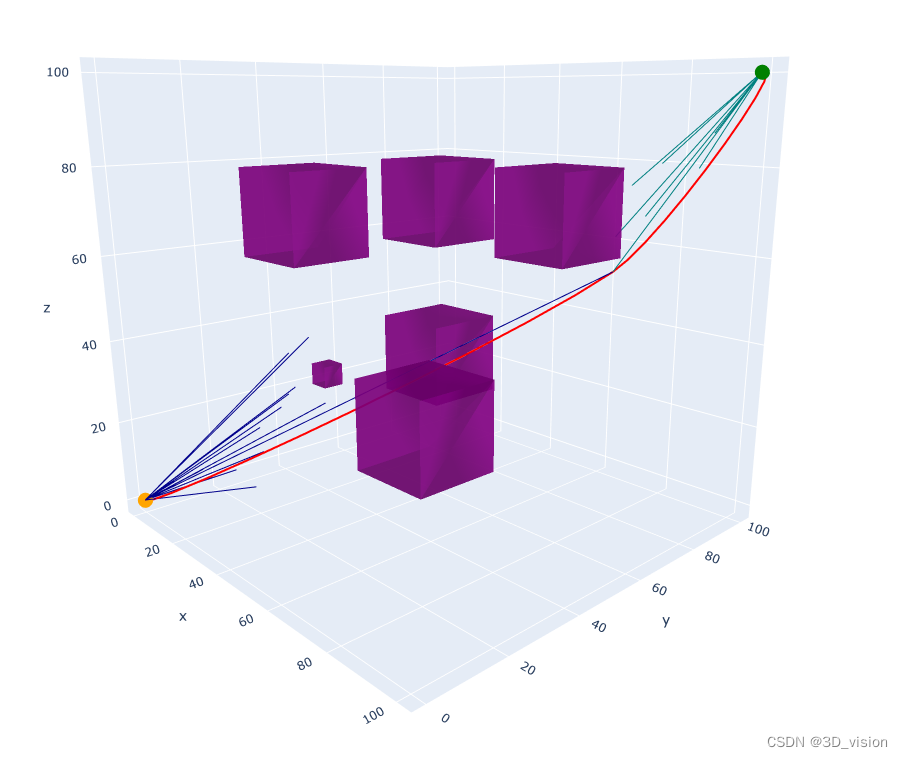
扩展到三维
因为机械臂的工作空间不是在一个平面内,而是在三维空间中,因此需要将RRT*算法和贝塞尔平滑优化算法扩展到三维空间,其实很简单,就是简单的进行一个维度扩充就可以了,这里不仔细讲了,贴一下自己做出来的效果图: