优化算法 学习记录

相关资料

李沐 动手学深度学习

优化算法

优化算法使我们能够继续更新模型参数，并使损失函数的值最小化。优化算法的性能直接影响模型的训练效率。

优化问题中大多数目标函数都很复杂，没有解析解。相反，必须使用数值优化算法。

• 优化与深度学习之间的关系
  • 优化和深度学习的目标是根本不同的。前者关注的是最小化目标，后者则关注在给定有限数量的情况下寻找合适的模型。
  • 训练误差和泛化误差通常不同：由于优化算法的目标函数通常是基于训练数据集的损失函数，因此优化的目标是减少训练误差。但是，深度学习（或更广义地说，统计推断）的目标是减少泛化误差。为了实现后者，除了使用优化算法来减少训练误差之外，我们还需要注意过拟合。
• 深度学习中使用优化的挑战
  • 这里关注局部最小值、鞍点和梯度消失
    • 鞍点：saddle point, 函数的所有梯度都消失但不是全局最小值也不是局部最小值的任何位置。较高维度的鞍点可能会更加隐蔽。
      
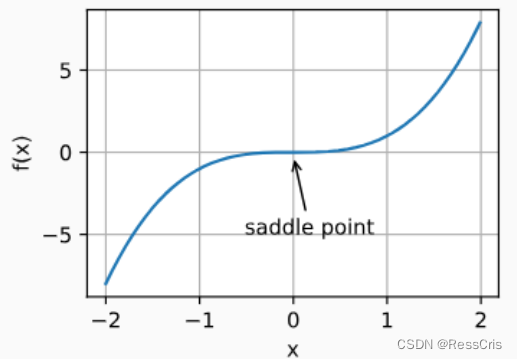
    • 梯度消失。假设我们想最小化函数 $$f(x)=tanh(x)$$
      ，然后我们恰好从 x=4 开始。正如我们所看到的那样，f 的梯度接近零。更具体地说，$f^{{}^{\prime }}(x)=1-tan{h}^2(x)$，因此 $f^{{}^{\prime }}(4)=0.0013$.
      

惩罚的概念

梯度下降

在凸问题背景下设计和分析算法是非常有启发性的。
凸优化的入门，以及凸目标函数上非常简单的随机梯度下降算法的证明。
为什么梯度下降算法可以优化目标函数？

学习率

学习率（learning rate）决定目标函数能否收敛到局部最小值，以及何时收敛到最小值。

牛顿法

随机梯度下降

目标函数通常是训练数据集中每个样本的损失函数的平均值。

给定 n 个样本的训练数据集，我们假设 $f_i(x)$是关于索引 $i$ 的训练样本的损失函数，其中 $X$ 是参数向量。然后我们得到目标函数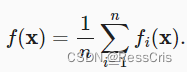
$X$的目标函数的梯度计算为

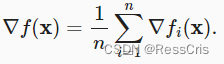
其中$\mu$是学习率。我们可以看到，每次迭代的计算代价从梯度下降的$O(n)$降至常数$O(1)$.

小批量随机梯度下降

动量法

这个动量法似乎不是针对学习率的改变。而是针对每个 $x_i$ 的值。

动量法可以解决变量之间梯度变化不一致导致的一些问题：

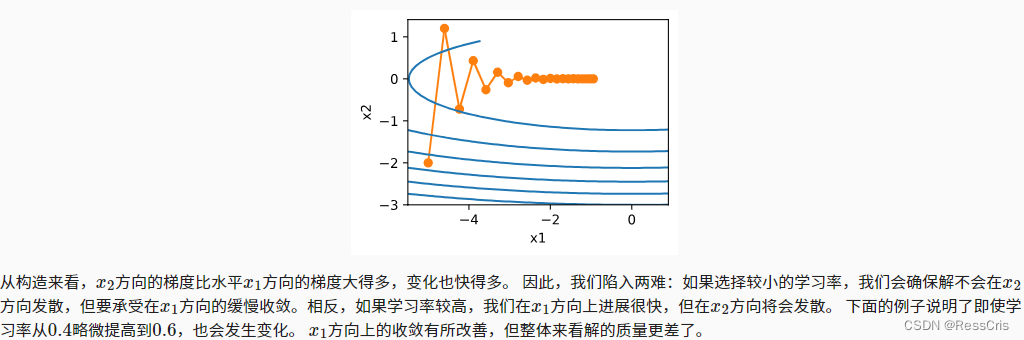
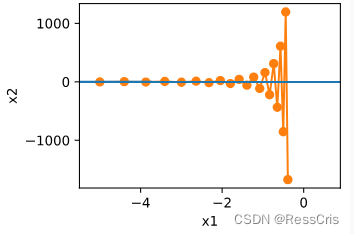
动量法解决上述问题

AdaGrad 算法

在AdaGrad算法中，我们允许每个坐标有单独的学习率。

然而，在深度学习中，我们可能希望更慢地降低学习率。 这引出了许多AdaGrad算法的变体。
优化算法本身会根据梯度调节其实际的学习率。

RMSProp算法

以RMSProp算法作为将速率调度与坐标自适应学习率分离的简单修复方法。

Adam

学习率调度器

多项式衰减
分段常数表

余弦学习率调度

它所依据的观点是：我们可能不想在一开始就太大地降低学习率，而且可能希望最终能用非常小的学习率来“改进”解决方案。

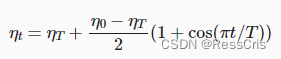
预热

在某些情况下，初始化参数不足以得到良好的解。 这对某些高级网络设计来说尤其棘手，可能导致不稳定的优化结果。 对此，一方面，我们可以选择一个足够小的学习率， 从而防止一开始发散，然而这样进展太缓慢。 另一方面，较高的学习率最初就会导致发散。

解决这种困境的一个相当简单的解决方法是使用预热期，在此期间学习率将增加至初始最大值，然后冷却直到优化过程结束。

class CosineScheduler:
    def __init__(self, max_update, base_lr=0.01, final_lr=0,
               warmup_steps=0, warmup_begin_lr=0):
        self.base_lr_orig = base_lr
        self.max_update = max_update
        self.final_lr = final_lr
        self.warmup_steps = warmup_steps
        self.warmup_begin_lr = warmup_begin_lr
        self.max_steps = self.max_update - self.warmup_steps

    def get_warmup_lr(self, epoch):
        increase = (self.base_lr_orig - self.warmup_begin_lr) \
                       * float(epoch) / float(self.warmup_steps)
        return self.warmup_begin_lr + increase

    def __call__(self, epoch):
        if epoch < self.warmup_steps:
            return self.get_warmup_lr(epoch)
        if epoch <= self.max_update:
            self.base_lr = self.final_lr + (
                self.base_lr_orig - self.final_lr) * (1 + math.cos(
                math.pi * (epoch - self.warmup_steps) / self.max_steps)) / 2
        return self.base_lr

scheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])


scheduler = CosineScheduler(20, warmup_steps=5, base_lr=0.3, final_lr=0.01)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])