梯度消失问题
目录
什么是梯度消失
梯度消失问题( vanishing gradient)是在早期的BP网络中比较常见的问题。这种问题的发生会让训练很难进行下去，看到的现象就是训练不再收敛——Loss过早地不再下降,而精确度也过早地不再提高。
梯度消失产生的原因
我们还是来看一个具体的例子:
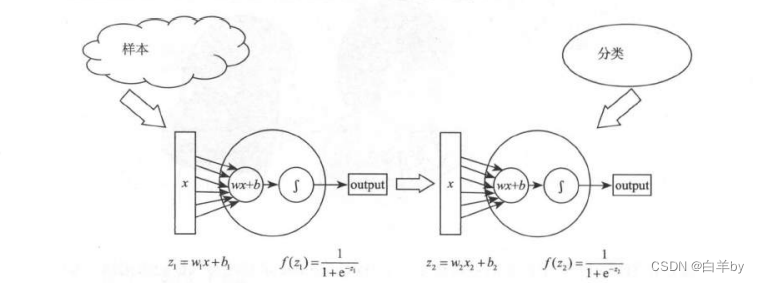
就是两个节点首尾相接组成的神经网络(应该说连“线”都算不上)，这其中位于网络前部的w1的更新就需要计算损失函数对w,的偏导数，在这个函数里，根据链式法则我们能够得到,前面的这个神经元的w,的导数是这样一个表达式:
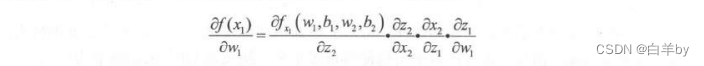
其中我们发现第一项关于中z_2的偏导数和第三项关于z_1的偏导数其实就是Sigmoid函数的斜率，Sigmoid函数的图像如图
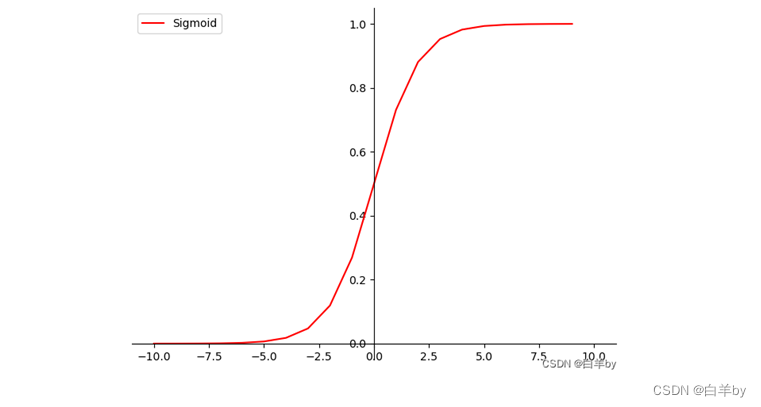
Sigmoid函数比较致命的缺点就是在自变量处于小于-5或者大于5的部分，他的斜率几乎处于水平了，即导数几乎为零，这就像一个陷阱，万一我们上面所说的第一项关于中z_2的偏导数和第三项关于z_1的偏导数正好处于陷阱时，会使整个导数的值也是接近0的状态，这样误差在向前传递的过程中会导致网络前端的w几乎没什么变化，因为单数实在是太小了，多个网络层的的导数连乘，从而越来越小，而且网络层级越多，越往前的隐藏层这种情况就越糟糕———w变化就越慢,也就是说，这一层没能学到什么东西。这就是我们所说的梯度消失问题，也叫作梯度弥散问题。
既然我们弄清楚了，导致梯度消失问题的原因是因为在对参数求偏导时，根据链式法则得到的连乘式中多个几乎为0的导数值连乘导致，那么我们就可以提出相应的解决办法。
导数小导致每次更新时的值过小，那么相反，导数大就应该会使更新的数值比较大，更新速度比较快。所以无非就是要消除这种链式发着中发生的每一项绝对值小于1的情况呗。
让我们再来看一下例子中的两个导数值：
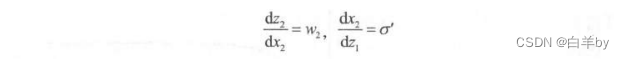
第二项其实就是sigmoid函数求导，即
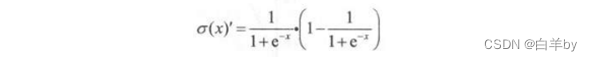
所以在这里我们的想法就是让连乘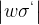
大于等于1。
梯度消失解决方法
我们可以尝试一下如下方法
方法1：将w初始化大一些
假设我们把w初始化成10，在 Sigmoid函数为0的地方，导数的绝对值是4,当 lwl=10的时候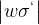
=2.5。这个值确实够大了，但是大就一定好么，未必。
同样是链式法则的连乘关系，原来是因为导数太小导致网络前端的w变化太慢，这么一改之后反过来了，网络前端的变化率太高了，一次的变化量非常大。就拿刚刚这个例子来说，如果有10层，10个2.5相乘就是9536左右。俗话说“过犹不及”，这就算是一个很小的n也能一下子从地下挪到天上去，这种现象叫做梯度爆炸( gradient explording)，也叫作梯度膨胀。
综上可知，这种方法似乎并不理想，那让我们看下一个方法。
方法二：选取合适的激活函数
既然sigmoid函数本身就有缺陷，那么我们就从根上解决问题，直接换激活函数！那是否有合适的激活函数呢？还真有，那就是ReLU激活函数，ReLU激活函数的图像如下
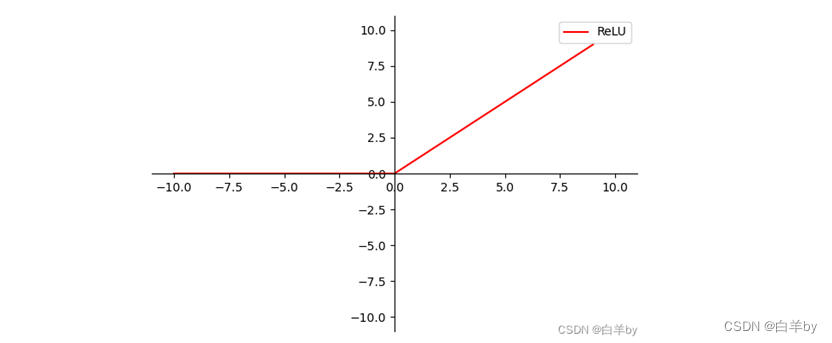
这个函数的形式为y=max(x,0)，这个函数在原点左侧部分斜率为0，在右侧则是一条斜率为1的直线。函数在x大于0的部分是呈现出线性特点的，在小于0的时候则是一条直线，这个锋利的弯折提供了良好的非线性特点。尤其注意它在第一象限的这条直线，它的导数恒为.1，这是它的“激活”状态;x小于0的部分导数恒为0，这是它的“非激活”状态。所以它的优点有两个应该是显而易见的。
其一，在第一象限中不会有明显的梯度消失问题，因为导数恒为1，而w在初始化的时候也是有大有小，连乘的时候不会轻易出现很小或者很大的数值，这就是一个非常好的特性了。
其二，由于导数为1，所以求解它的导数要比求解Sigmoid函数的导数代价要小一些，这里说的代价主要是时间代价。前面咱们说了求导数要在函数的这个点上用Loss(w+A)-Loss(x)的古社击求这个计算的次数可就比直接拿一个1出来麻烦多了，尤其是在损失函数里的w很多的时候，一次计算所消耗的计算资源就太多了，速度会变慢。