matlab axis函数_MATLAB二维图形

7.2.5  双坐标图和子图

本小节介绍双坐标图形的绘制方法。另外前面已经有例子涉及了子图的绘制，读者应该有所了解，本小节将详细介绍子图的绘制方法。

1．双坐标图

在实际应用中，常常会提出这样一种需求：把同一自变量的两个不同量纲、不同数量级的函数量的变化绘制在同一张图上。例如希望在同一张图上表现温度、湿度随时间的变化；温度、压力的响应曲线；人口数量、GDP的变化曲线；放大器输入、输出电流变化曲线等。为满足这种需求，MATLAB提供了以下几个命令。

(1)plotyy(X1,Y1,X2,Y2)：以左右不同纵轴绘制X1-Y1、X2-Y2两条曲线。

(2)plotyy(X1,Y1,X2,Y2,function)：以左右不同纵轴，把X1-Y1、X2-Y2绘制成function指定形式的两条曲线。

(3)plotyy(X1,Y1,X2,Y2,'function1','function2') 以左右不同纵轴，把X1-Y1、X2-Y2绘制成function1、function2指定的不同形式的两条曲线。

(4)[AX,H1,H2] = plotyy(...)：函数plotyy将创建的坐标轴句柄保存到返回参数AX中，将绘制的图形对象句柄保存在返回参数H1和H2中。其中，AX(1)中保存的是左侧轴的句柄值，AX(2)中保存的是右侧轴的句柄值。

【例7-12】  双坐标轴绘图示例。

Ex_7_12.m

clear

x = 0:0.01:20;                                %  x坐标

y1 = 200*exp(-0.05*x).*sin(x);             %  Y1

y2 = 0.8*exp(-0.5*x).*sin(10*x);           %  Y2

[AX,H1,H2] = plotyy(x,y1,x,y2,'plot');     %  绘制双坐标轴图形

set(get(AX(1),'Ylabel'),'String','Slow Decay')   %  纵轴标签1

set(get(AX(2),'Ylabel'),'String','Fast Decay') %  纵轴标签2

xlabel('Time (\musec)')                       %  x标签

title('Multiple Decay Rates')                %  图形标题

set(H1,'LineStyle','--')                      %  线形1

set(H2,'LineStyle',':')                       %  线形2

以上代码运行的结果如图7-15所示。

2．子图

MATLAB允许用户在同一个图形窗口内布置几幅独立的子图，具体的调用语法如下。

(1)subplot(m,n,P)：使(m x n)幅子图中的第k幅成为当前幅。子图的编号顺序是左上方为第1幅，向右向下依次排序。

(2)subplot('Position',[left bottom width height])：在指定位置上绘制子图，并成为当前图。

【例7-13】  subplot函数调用示例1。

Ex_7_13.m

clf;clear

t=(pi*(0:1000)/1000)';

y1=sin(t);y2=sin(10*t);y12=sin(t).*sin(10*t);

subplot(2,2,1),plot(t,y1);axis([0,pi,-1,1])

subplot(2,2,2),plot(t,y2);axis([0,pi,-1,1])

subplot('position',[0.2,0.05,0.6,0.45])

plot(t,y12,'b-',t,[y1,-y1],'r:');axis([0,pi,-1,1])

以上代码运行的结果如图7-16所示。

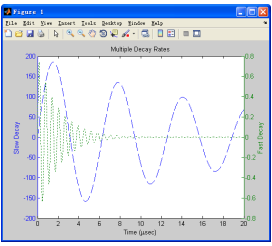
图7-15  双坐标轴绘图示例

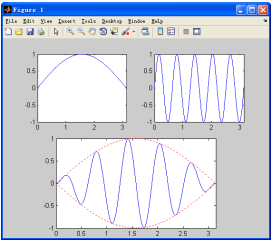
图7-16  子图的绘制(1)

【例7-14】  subplot函数调用示例2。

Ex_7_14.m

figure

for i=1:12

    subplot(12,1,i)                    %  子图位置

    plot (sin(1:100)*10^(i-1))       %  绘制图形

    set(gca,'xtick',[],'ytick',[])   %  设置坐标轴

end

set(gca,'xtickMode', 'auto')          % 重新设置最底层子图的x轴

以上代码运行的结果如图7-17所示。

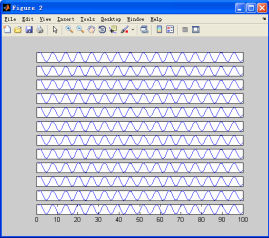
图7-17  字图的绘制(2)

7.2.6  双轴对数图形

在实际中，我们经常需要绘制坐标轴为对数的图形。所谓双轴对数图形，就是指两个坐标轴都是对数坐标，这需要用到loglog函数，其具体调用语法如下。

(1)loglog(Y)：如果参数Y为实数向量或矩阵，则根据Y列向量与它们的指数绘制图形。如果Y为复数向量或矩阵，loglog(Y)则等价于loglog(real(Y),imag(Y))，在loglog的其他调用形式中将忽略Y的虚数部分。

(2)loglog(X1,Y1,...,Xn,Yn)：根据参数Xn与Yn匹配的数据绘制双轴对数图形。如果只有Xn或Yn为矩阵，则函数将绘制向量对矩阵行或列的图形，行向量的维数等于矩阵的列数，列向量的维数等于矩阵的行数。

(3)loglog(X1,Y1,LineSpec,...)：将按顺序分别绘出按3个参数Xi、Yi和LineSpec绘制的对数图形。其中参数LineSpec指明了线条的类型、标记符号和绘制线用的颜色。

(4)loglog(...,'PropertyName',PropertyValue,...)：对所有由loglog函数创建的图形对象句柄的属性进行设置。

(5)h = loglog(...)：返回值为图形对象句柄向量，一个句柄对应一条直线。

【例7-15】  loglog绘图示例。在区间到之间绘制函数双轴对数图形。

Ex_7_15.m

x = logspace(-1,2);       %  生成50个等对数间距的坐标

loglog(x,exp(x),'-s')

grid on

运行的结果如图7-18所示。

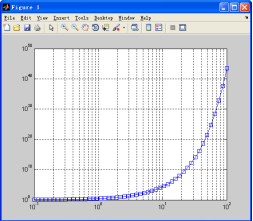
图7-18  双轴对数图形

7.2.7  特殊二维图形

1．条形图

在MATLAB中使用函数bar和barh来绘制二维条形图，分别绘制纵向和横向图形。这两个函数的用法相同。默认情况下，用bar函数绘制的条形图将矩阵中的每个元素均表示为“条形”，横坐标为矩阵的行数，“条形”的高度表示元素值。其调用语法如下。

(1)bar(Y)：对Y绘制条形图。如果Y为矩阵，Y的每一行数据所对应的条形图聚集在一起，座落在相对应的横坐标上。横坐标表示矩阵的行数，纵坐标表示矩阵元素值的大小。

(2)bar(...,width)：指定每个条形的相对宽度。条形的默认宽度为0.8。

(3)bar(...,'style')：指定条形的样式。style的取值为grouped或者stacked，默认为grouped。其中，grouped表示绘制的图形共有m组，其中m为矩阵Y的行数，每一组有n个条形，n为矩阵Y的列数，Y的每个元素对应一个条形。stacked表示绘制的图形有m个条形，每个条形为第m行的n个元素的和，每个条形由多个(n个)色彩构成，每个色彩对应相应的元素。

(4)bar(...,'bar_color')：指定绘图的色彩，bar_color的取值与plot绘图的色彩相同。

(5)bar(axes_handles,...)，barh(axes_handles,...)：在指定的坐标轴上绘制。

【例7-16】  使用bar函数与barh函数绘图示例。

Ex_7_16.m

Y = round(rand(5,3)*10);%随机产生一个5×3矩阵，每个元素为1-10之间的整数

subplot(2,2,1)       %设定绘图区域，在图形对象的左上角绘制

bar(Y,'group')       %绘制纵向条形图

title 'Group'        %添加标题Group

subplot(2,2,2)       %在图形对象的右上角绘制

bar(Y,'stack')

title 'Stack'

subplot(2,2,3)       %在图形对象的左下角绘制

barh(Y,'stack')      %绘制横向条形图

title 'Stack'

subplot(2,2,4)       %在图形对象的右下角绘制

bar(Y,7.5)

title 'Width = 7.5'

运行的结果如图7-19所示。

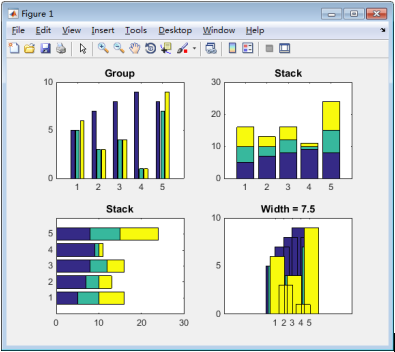
图7-19  条形图示例

2．区域图

区域图在显示向量或是矩阵中的元素在x轴的特定点占所有元素的比例时十分直观。默认情况下，函数area将矩阵中各行的元素集中，将这些值绘成曲线，并填充曲线和x轴之间的空间。其调用语法如下。

(1)area(Y)：绘制向量Y或矩阵Y各列的和。

(2)area(X,Y)：若X和Y是向量，则以X中的元素为横坐标、Y中元素为纵坐标绘制图像，并且填充线条和x轴之间的空间；如果Y是矩阵，则绘制Y每一列的和。

(3)area(...,basevalue)：设置填充的底值，默认为0。

(4)area(...,'PropertyName',PropertyValue,...)：对所有由area函数创建的图形对象句柄的属性进行设置。

(5)area(axes_handle,...)：在指定的坐标轴上绘制。

(6)h = area(...)：返回area图形对象的句柄值。

【例7-17】  area函数调用示例。

本例将Y中的数据绘制成为了区域图。每一列数据在绘制的时候都是在前一列的基础上累加的，即最下面一条折线绘制的是第1列的数据，而第2列与第1列的和是中间折线的数据源，依次类推。如此就可以看出数据中每一列所占的比例。

Ex_7_17.m

Y = [1, 5, 3;

     3, 2, 7;

     1, 5, 3;

     2, 6, 1];

area(Y)

grid on

colormap summer       %  设置颜色

set(gca,'Layer','top')

title 'Stacked Area Plot'      %  图名

运行的结果如图7-20所示。

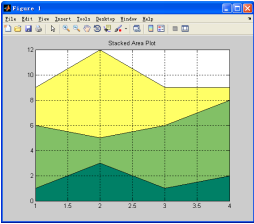
图7-20  区域图示例

3．饼形图

在统计学中，经常要使用饼形图来表示各个统计量占总量的份额，饼形图可以显示向量或矩阵中的元素占总体的百分比。在MATLAB中可以使用pie函数来绘制二维饼形图，其调用语法如下。

(1)pie(X)：绘制X的饼形图，X的每个元素占有一个扇形，其顺序为从饼形图上方正中开始，逆时针为序，分别为X的每个元素；如果X为矩阵，则按照各列的顺序排列。在绘制时，如果X的元素之和大于1，则按照每个元素所占的百分比绘制；如果元素之和小于1，则按照每个元素的值绘制，绘制出一个不完整的饼形图。

(2)pie(X,explode)：参数explode设置相应的扇形偏离整体图形，用于突出显示。explode必须与X具有相同的维数。explode和X的分量对应，若其中有分量不为零，则X中的对应分量将被分离出饼形图。

(3)pie(...,labels)：标注图形，labels为字符串元胞数组，元素的个数必须与X的个数相同。

(4)pie(axes_handle,...)：在指定的坐标轴上绘制。

(5)h = pie(...)：返回pie图形对象的句柄值。

【例7-18】  绘制二维饼形图示例。使用函数pie绘制二维饼形图，并突出向量中的某个元素。

Ex_7_18.m

x = [1 3 0.5 2.5 2];

explode = [0 1 0 0 0];         %  突出显示第2个元素

pie(x,explode)

colormap jet

运行的结果如图7-21所示。

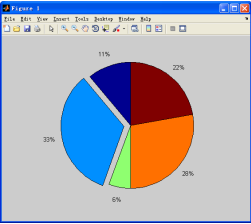
图7-21  饼形图示例

4．直方图

直方图用于直观地显示数据的分布情况。在MATLAB中有两个函数可用于绘制直方图：hist和rose，分别用于在直角坐标系和极坐标系中绘制直方图。hist函数的应用更广泛一些，这里只介绍hist函数的用法。关于rose函数，有兴趣的读者可以参阅MATLAB的帮助文档。hist函数的调用语法如下。

(1)n = hist(Y)：绘制Y的直方图。

(2)n = hist(Y,x)：指定直方图的每个分格，其中x为向量，绘制直方图时，以x的每个元素为中心创建分格。

(3)n = hist(Y,nbins)：指定分格的数目。

【例7-19】  hist函数绘制直方图示例。

Ex_7_19.m

x = -4:0.1:4;

y = randn(10000,1);

hist(y,x)

h = findobj(gca,'Type','patch');

set(h,'FaceColor','r','EdgeColor','w')         %  设置边界和填充颜色

以上代码运行的结果如图7-22所示。

5．离散型数据图

在MATLAB中，可以使用函数stem和stairs绘制离散数据，分别生成二维离散图形和二维阶跃图形。stem函数调用语法如下。

(1)stem(Y)：绘制Y的数据序列，图形起始于X轴，并在每个数据点处绘制一个小圆圈。

(2)stem(X,Y)：按照指定的X绘制数据序列Y。

(3)stem(...,'fill')：指定是否给数据点处的小圆圈着色。

(4)stem(...,LineSpec)：设置绘制的线型、标示符号和颜色。

【例7-20】  使用stem函数绘制离散图形。在区间绘制二维离散图形，设置其线型为虚线，并对数据点处着色。

Ex_7_20.m

t = linspace(-2*pi,2*pi,10);   %  创建10个位于-2*pi到2*pi之间的等间隔的数

h = stem(t,cos(t),'fill','--');     %  以'--'绘制离散数据图

set(get(h,'BaseLine'),'LineStyle',':')

set(h,'MarkerFaceColor','red')

以上代码运行的结果如图7-23所示。

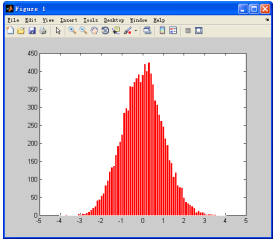
图7-22  直方图示例

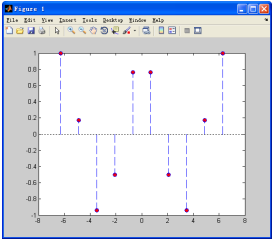
图7-23  离散性数据图示例

stairs函数用来绘制二维阶跃图形，其调用语法如下。

(1)stairs(Y)：按照向量Y的元素绘制阶跃图形。

(2)stairs(X,Y)：按照指定X对应的向量Y中的元素绘制出阶跃图形，其中X必须为单调递增。

stairs还有其他与stem调用语法相同的语法，这里不再赘述。

【例7-21】  使用stairs函数绘制正弦波的阶跃图形。在区间()绘制正弦波的阶跃图形。

Ex_7_21.m

x = linspace(-2*pi,2*pi,40); %  创建40个位于-2*pi到2*pi之间的等间隔的数

stairs(x,sin(x))                %  绘制正弦曲线的二维阶跃图形

以上代码运行的结果如图7-24所示。

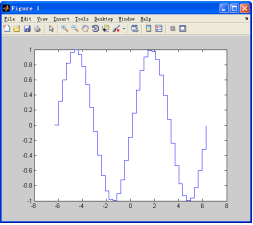
图7-24  二维阶跃图形示例

6．方向矢量图和速度矢量图

在MATLAB中可以绘制方向矢量图和速度矢量图，用于绘制这两种矢量图的函数如表7-9所示。

表7-9MATLAB中用于绘制方向矢量图和速度矢量函数

函    数	功    能
compass	罗盘图，绘制极坐标图形中的向量
feather	羽状图，绘制向量，向量起点位于与x轴平行的直线上，长度相等
quive	二维矢量图，绘制二维空间中指定点的方向矢量

在上述函数中，矢量由一个或两个参数指定，指定矢量相对于圆点的x分量和y分量。如果输入一个参数，则将参数视为复数，复数的实部为x分量，虚部为y分量；如果输入两个参数，则分别为向量的x分量和y分量。

compass函数用来绘制罗盘图，其调用语法如下。

(1)compass(U,V)：绘制罗盘图，数据的x分量和y分量分别由U和V指定。

(2)compass(Z)：绘制罗盘图，数据由Z指定。

(3)compass(...,LineSpec)：设置绘制的线型、标示符号和颜色。

(4)compass(axes_handle,...)：在指定的坐标轴上绘制。

(5)h = compass(...)：绘制罗盘图，并返回图形句柄。

【例7-22】  绘制矩阵的本征值的罗盘图示例。

Ex_7_22.m

Z = eig(randn(20,20));          %  求20×20随机矩阵的本征值

compass(Z)

以上代码运行的结果如图7-25所示。

feather函数用来绘制羽状图，其调用语法如下。

(1)feather(U,V)：绘制羽状图，数据的x分量和y分量分别由U和V指定。

(2)fetaher(Z)：绘制羽状图，数据由Z指定。

(3)feather(...,LineSpec)：设置绘制的线型、标示符号和颜色。

(4)feather(axes_handle,...)：在指定的坐标轴上绘制。

(5)h = feather(...)：绘制羽状图，并返回图形句柄。

【例7-23】  使用feather函数绘制羽状图示例。

Ex_7_23.m

theta = (-90:10:90)*pi/180;    %  生成数据

r = 2*ones(size(theta));        %  生成与theta相同宽度和高度的矩阵

[u,v] = pol2cart(theta,r);      %  将极坐标数据theta和r转换成直角坐标u,v

feather(u,v);

以上代码运行的结果如图7-26所示。

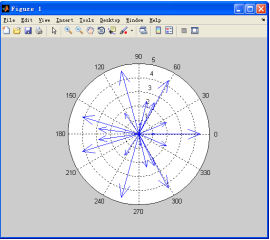
图7-25  使用compass函数绘制罗盘图示例

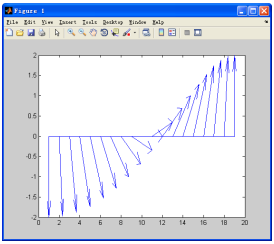
图7-26  使用feather函数绘制羽状图示例

quiver函数用来绘制箭状图或者速度矢量图，其调用语法如下。

(1)quiver(x,y,u,v)：绘制矢量图，参数x和y用于指定矢量的位置，u和v用于指定要绘制的矢量。

(2)quiver(u,v)：绘制矢量图，矢量的位置为默认值。

(3)quiver(...,scale)：自动调整箭头的比例以适合网格，然后用因子scale拉伸箭头。

【例7-24】  绘制函数的梯度图。

梯度方向也就是速度方向，本例使用quiver函数即可达到目的。

Ex_7_24.m

[X,Y] = meshgrid(-2:.2:2);%  生成网格数据

Z = X.*exp(-X.^2 - Y.^2);    %  定义函数Z

[DX,DY] = gradient(Z,.2,.2); %  求Z在X和Y方向的梯度

contour(X,Y,Z)               %  绘制Z的等高线

hold on                      %  打开图形保持

quiver(X,Y,DX,DY)

colormap hsv           %  创建颜色图

hold off                       %  关闭图形保持

以上代码运行的结果如图7-27所示。

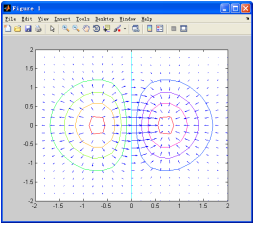
图7-27  梯度图示例

7．等高线的绘制

等高线用于创建、显示并标注由一个或多个矩阵确定的等值线。MATLAB中提供了一些函数用于绘制等高线，如表7-10所示。

表7-10MATLAB中用于绘制等高线的函数及其功能

函 数 名	功    能	函 数 名	功    能
clabel	使用等值矩阵生成标注，并将标注显示在当前图形	contourc	用于计算由其他等高线函数调用的等值矩阵
contour	显示矩阵Z的二维等高线图	meshc	创建一个匹配有二维等高线图的网格图
contourf	显示矩阵Z的二维等高线图，并在各等高线之间用实体颜色填充	surfc	创建一个匹配有二维等高线图的曲面图

这里只介绍最常用的函数contour，其他函数请读者自行查阅帮助文档。contour函数用于绘制二维等高线图，其调用语法如下。

(1)contour(Z)：绘制矩阵Z的等高线，绘制时将Z在x-y平面上插值，等高线数量和数值由系统根据Z自动确定。

(2)contour(Z,n)：绘制矩阵Z的等高线，等高线数目为n。

(3)contour(Z,v)：绘制矩阵Z的等高线，等高线的值由向量v决定。

(4)contour(X,Y,Z)：绘制矩阵Z的等高线，坐标值由矩阵X和Y指定，矩阵X、Y、Z的维数必须相同。

(5)contour(...,LineSpec)：利用指定的线型绘制等高线。

(6)[C,h] = contour(...)：绘制等高线，并返回等高线矩阵和图形句柄。

【例7-25】  绘制peaks函数的等高线。

peaks函数是系统自带的测试函数。

Ex_7_25.m

Z = peaks;

[C,h] = contour(interp2(Z,4));  %  绘制插值以后的等高线图，插值可以平滑曲线

text_handle = clabel(C,h);   %  等高线标注

set(text_handle,'BackgroundColor',[1 1 .6],...   %  设置颜色

'Edgecolor',[.7 .7 .7])

以上代码运行的结果如图7-28所示。

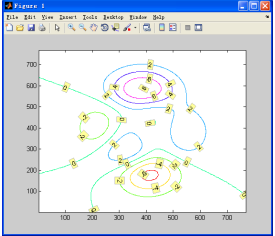
图7-28  peaks函数等高线图