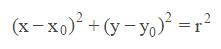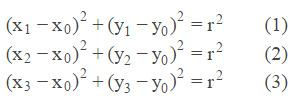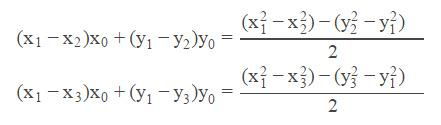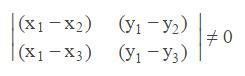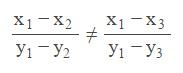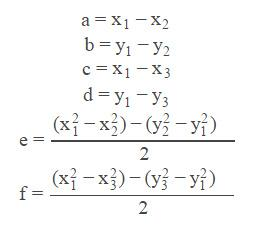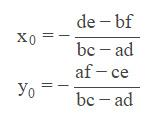三点确定圆的半径_51CAE_新浪博客

近日通过CAE软件分析弹性体折叠过程中的半径变化趋势，已经从分析结果文件中提取了弯折区域三点的运动轨迹，设想将弯折区域近似为圆弧并通过三点计算得出圆的半径。经网上查找一翻，发现一篇博客有比较详细的计算公式，由于不能直接转载，在此记录一篇作为笔记。为向原作者示敬，附上原作链接如下：http://blog.csdn.net/liyuanbhu/article/details/52891868

我们设一个圆的圆心坐标为 （x0，y0），半径为 r。那么这个圆的方程可以写为：

取圆上任意三点，设这三个点的坐标分别是 （x1，y1），（x2，y2），（x3，y3）。由于圆弧上所有点到圆心距离均为半径，那么有：

​公式（1）（2）相减，（1）（3）相减之后经过化简可以得到： 

x0，y0有唯一解的条件是系数行列式不为 0： 

简单变变型也就是： 

上式的几何意义即：三点不能共线。

设：

​那么 : 

有了x0和y0的值后，带入（1） 式就可以得到半径 r 的值。至此，三点确定圆的问题就解决了。

好了，有了以上理论以及计算公式，利用 Python 读入CAE软件计算得到的圆弧上三个点的运动轨迹，即可得到折叠过程中半径r的变化趋势了。

​

​