信号与线性系统翻转课堂笔记11——连续LTI系统频域分析
信号与线性系统翻转课堂笔记11——连续LTI系统频域分析
The Flipped Classroom11 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点)LTI连续系统频率响应的概念及其物理含义,理解滤波器的概念及其作用;
(2,重点)熟练掌握LTI系统频率响应与其他系统模型之间的相互转换;
(3)基于频域分析的方法,求LTI连续系统的零状态响应(含周期和非周期激励信号);
(4)无失真传输的概念,信号通过线性系统不失真的条件;
(5)了解理想低通滤波器及其冲激响应和阶跃响应的特点。
二、问题与解答
1、 将一个信号输入到系统,并得到相应输出信号的过程,就是对信号的处理。根据系统频率响应的物理含义,结合教材例题4.8-1,从频域的角度讨论:如果用一个LTI系统来处理信号,其实质是什么(与输入信号相比,处理的结果即输出信号的频率、幅度、相位等发生了什么变化,这些变化是由系统的什么特性决定的)?
2、根据预备训练二的内容,讨论:①从频域的角度来看,预备训练中给出的RC电路是一种什么类型(低通、高通、带通、带阻)的滤波器(可参考课件141页的幅频响应曲线来回答)?如果想利用一个电阻和一个电容来构建一个高通滤波器,电路应该如何连接?②RLC电路处于过阻尼状态时,是一种什么类型的滤波器?③RLC电路处于欠阻尼状态时,又属于什么类型的滤波器?
3、

4、

5、

6、

1、系统的频率响应
将一个信号输入到系统,并得到相应输出信号的过程,就是对信号的处理。根据系统频率响应的物理含义,结合教材例题4.8-1,从频域的角度讨论:如果用一个LTI系统来处理信号,其实质是什么(与输入信号相比,处理的结果即输出信号的频率、幅度、相位等发生了什么变化,这些变化是由系统的什么特性决定的)?


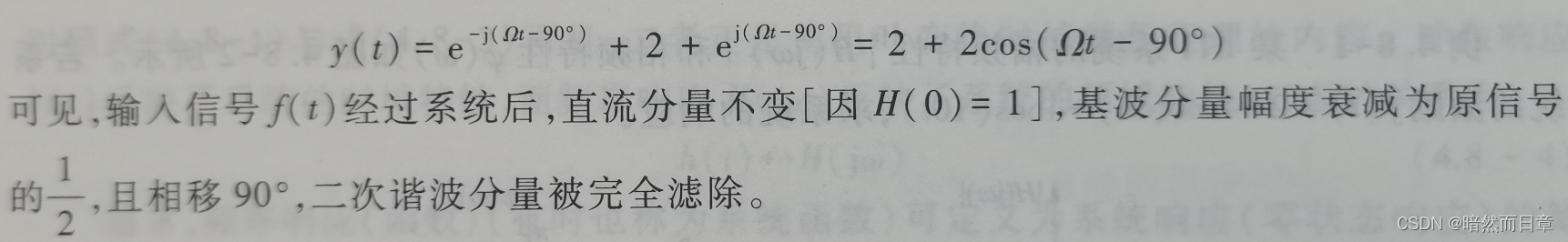
系统频率响应的物理含义:是LTI系统的一种系统模型,是系统冲激响应的h(t)的傅里叶变换。
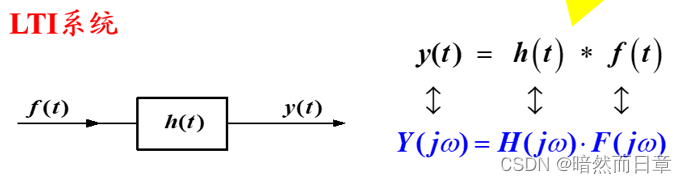
实质:

2、RC/RLC电路构建滤波器
根据预备训练二的内容,讨论:①从频域的角度来看,预备训练中给出的RC电路是一种什么类型(低通、高通、带通、带阻)的滤波器(可参考课件141页的幅频响应曲线来回答)?如果想利用一个电阻和一个电容来构建一个高通滤波器,电路应该如何连接?②RLC电路处于过阻尼状态时,是一种什么类型的滤波器?③RLC电路处于欠阻尼状态时,又属于什么类型的滤波器?
(1)
在基本的RC滤波电路中:C做输出瑞就是低通滤波器,R做输出就是高通滤波器。
当电源频率由0变大时,电容两端电压由大变小,因而低通;而在高通电路中,电阻两瑞的电压由0慢慢变大,因而高通。
因此给出的RC电路为为低通滤波器。
构建高通滤波器,需要将电阻作为输出端。
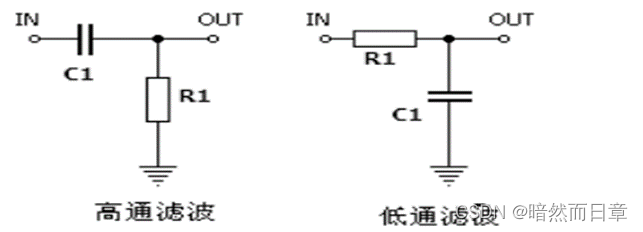
(2)
处于过阻尼状态时是低通滤波器。

(3)
处于欠阻尼状态时可以是低通滤波器,也可以是高通滤波器。
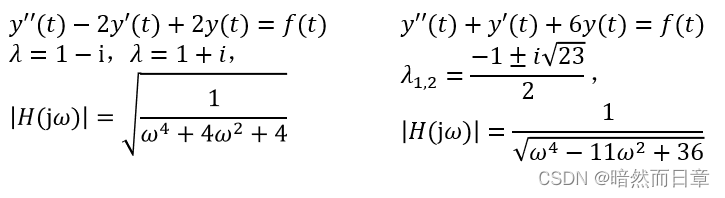
3、求频率响应、冲激响应、零状态响应


4、由冲激响应求微分方程


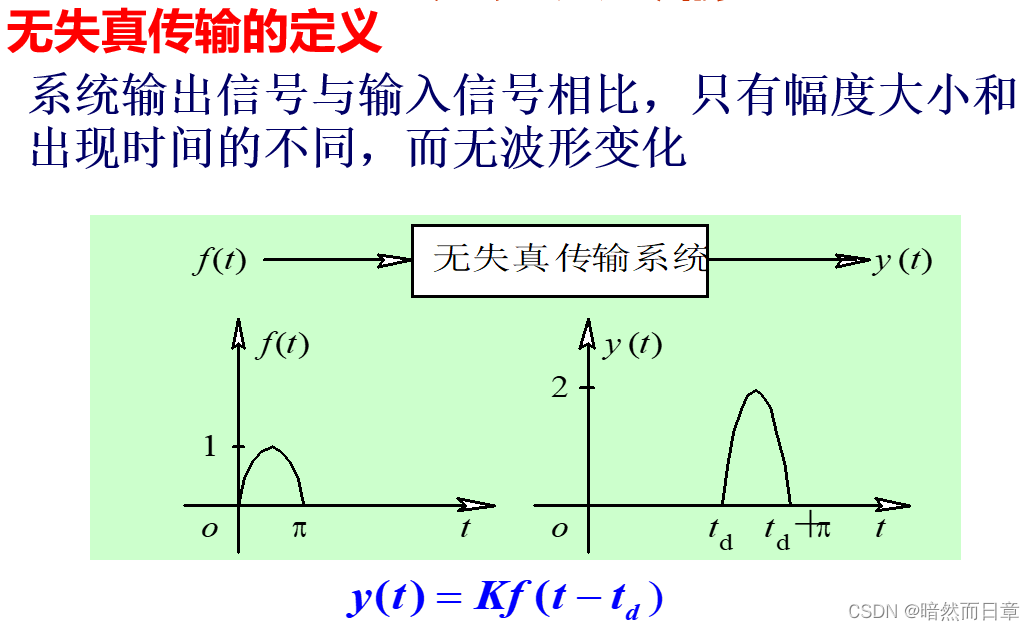
5、无失真传输


syms t w
f=cos(t)+cos(2*t);
y1=2*cos(t)+cos(2*t);
y2=cos(t+pi/4)+cos(2*t+pi/3);
y3=2*cos(t+pi/4)+cos(2*t+pi/2);
subplot(2,2,1);
fplot(t,f,[-10,10]);
grid on;title('f=cos(t)+cos(2*t)')
subplot(2,2,2);
fplot(t,y1,[-10,10])
;grid on;title('y1=2*cos(t)+cos(2*t)')
subplot(2,2,3);
fplot(t,y2,[-10,10]);
grid on;title('y2=cos(t+pi/4)+cos(2*t+pi/3)')
subplot(2,2,4);
fplot(t,y3,[-10,10]);
grid on;title('y3=2*cos(t+pi/4)+cos(2*t+pi/2)')
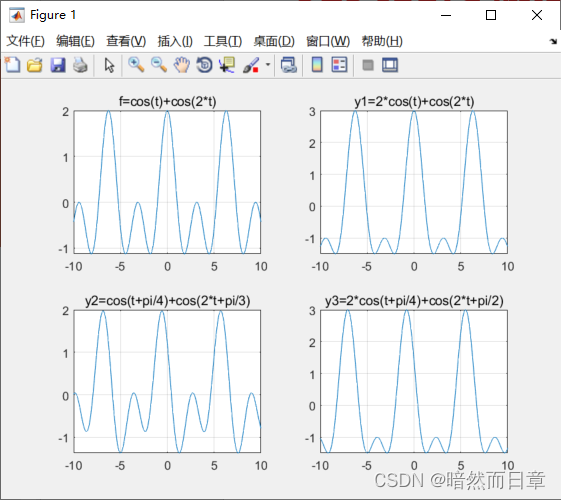
y1(t)相对于f(t)产生了幅度失真,即只有前面的cost变成了2cost,高频分量产生幅度失真,未产生相位失真。
y2(t)相对于f(t)产生了相位失真,cost发生线性移动π/4,cos2t发生线性移动π/3,未产生幅度失真。
y3(t)相对于f(t)既产生了相位失真,cost发生线性移动π/4,cos2t发生线性移动π/3,也产生了幅度失真,只有前面的cost变成了2cos(t+4/π)。
6、理想低通滤波器的冲激响应和阶跃响应

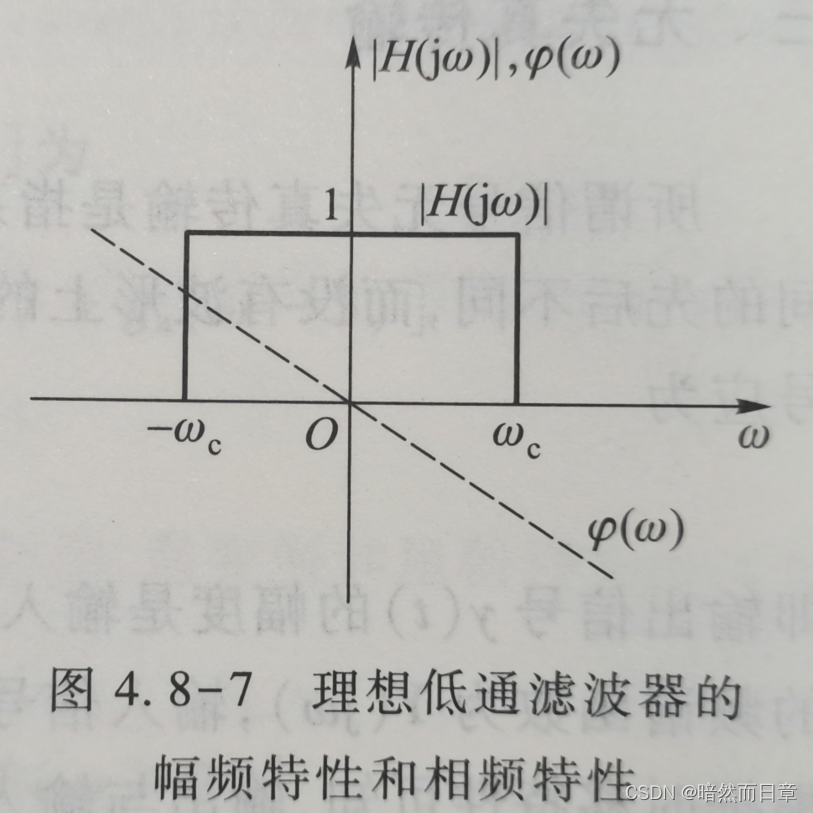
(1)
对于冲激响应来说,滤波器截止频率变高输出信号失真度下降。
对于阶跃响应来说,截止频率变高阶跃响应上升时间降低,失真度下降。
(2)
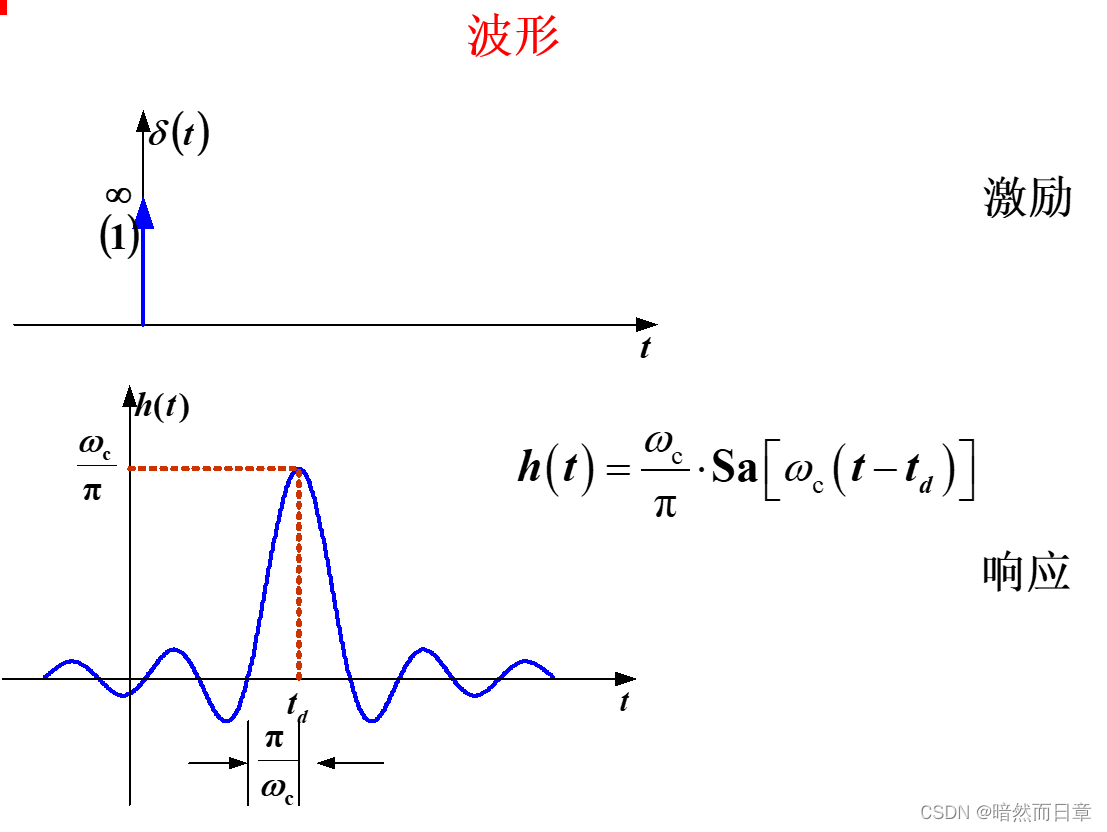
对于冲激响应,截止频率变高,w_c/π变大,π/w_c减小,失真度下降,波形越来越接近理想情况。
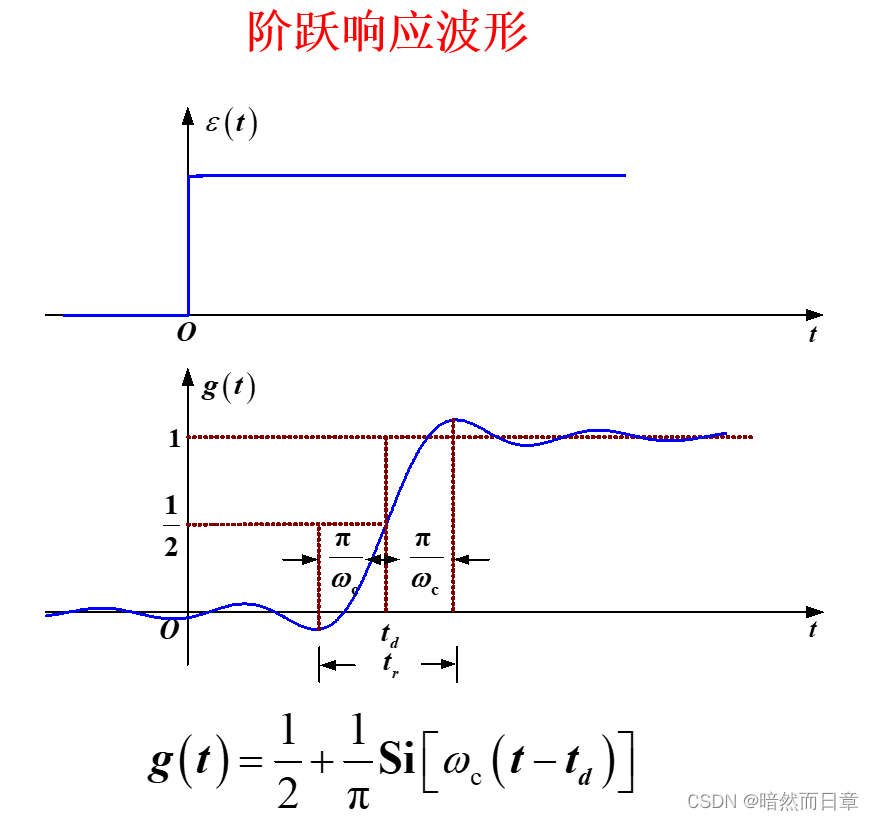
对于阶跃函数,截止频率变高,π/w_c减小,t_d系统延迟时间越小,上升时间t_r越小,系统通带变宽,失真度下降,波形越来越接近理想情况。