机器学习笔记三——强化学习的V值计算
一、蒙特卡诺采样回溯计算V值
把智能体放入环境的任意状态——从这个状态开始按照策略进行动作选择,并进入新状态——重复步骤2,直至进入最终状态——从最终状态往前回溯,计算每个状态的G值——重复1~4状态多次,平均每个状态的G值,这就是所需的V值
1.具体G值计算如下:
按照策略往后走,过程中不进行计算,只记录每一步的奖惩r
从终点往前走,到某一状态获得的奖励总和就是G值。此时G=r+gamma*G_1,即这一步的G值等于奖惩r加上上一步的G值(G_1)乘以一定的折扣率(小于1)。这个折扣率是因为认为未来的奖惩对当前的影响与现在的奖惩不等价。
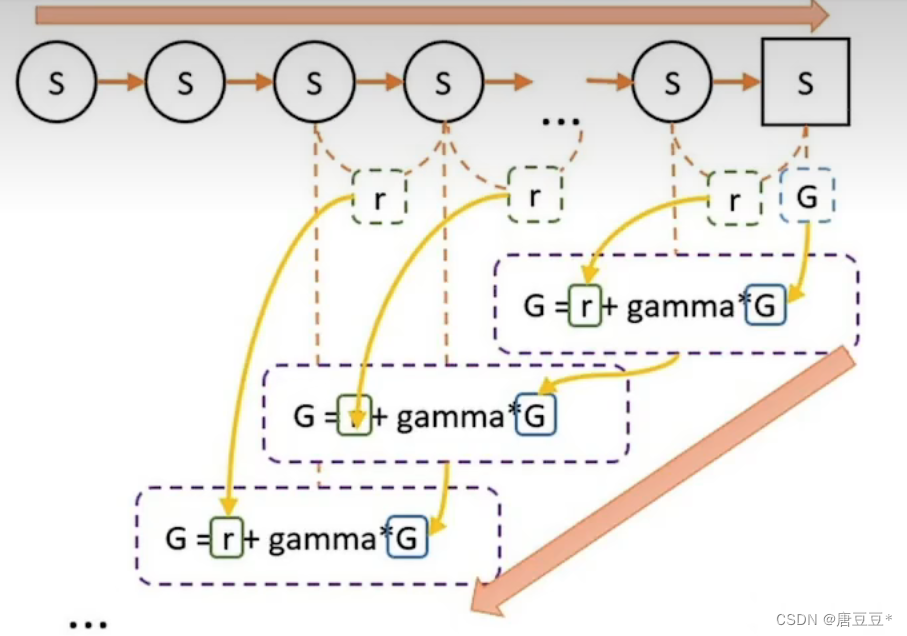
2.G值与V值得关系
每一个状态往后会有多条轨迹,走到状态终点。从终点往前回溯可以得到多个不同得G值,而V值是正是这个G值得平均值。但个状态对应的轨迹由于策略不同,选择的权重就不同,所以实际计算V值得时候需要将相应轨迹得G值乘以对应得权重。
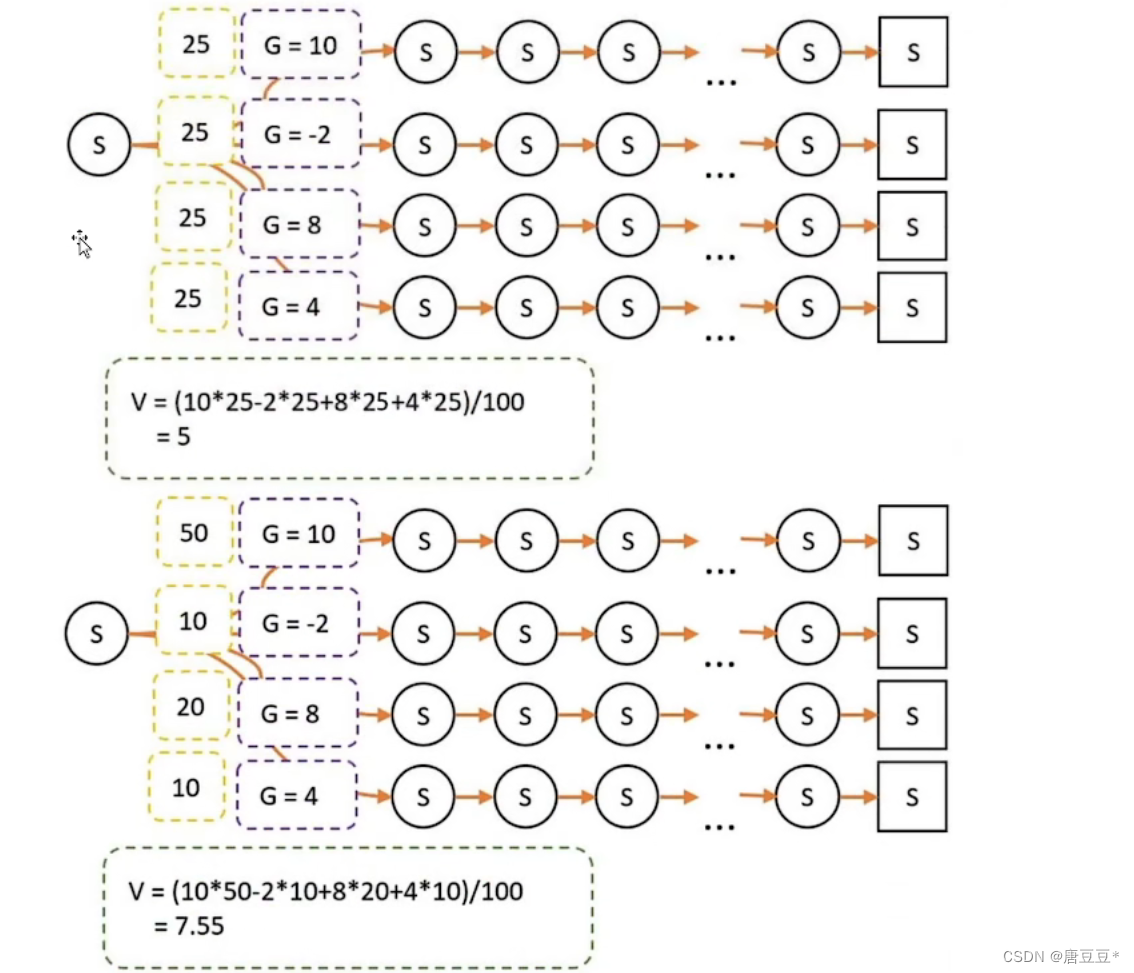
此方法:每一次都需要从前走到尾,再从后往前追溯,运行时间过长
二、蒙特卡诺和时序差分估算状态V值
1.蒙特卡洛估算状态V值
相当于每回来一个G值,对V值进行一次估算。
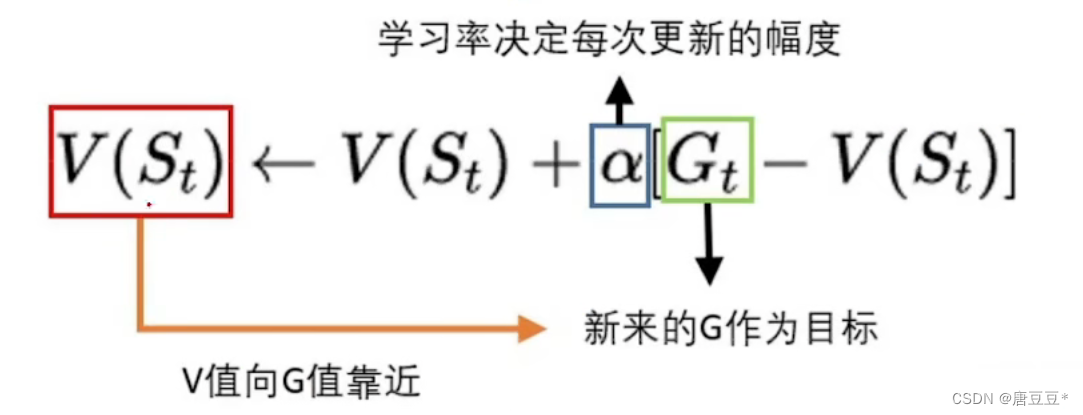
更新法本质:新平均=旧平均+步长*(新加入元素-旧平均)
步长就决定你调节得快慢,有点类似梯度下降法。不断更新拟合,调整次数越多,与实际得V值更接近。
但仍旧存在需要等轨迹跑到状态终点回溯,所以也可能时间较长。
2.时序差分估算状态V值(应用最为广泛)
只需要走N步,就开始回溯。
回溯时有可能有两种可能:
1)第N步的状态之前没有走过,此时认为V_N=0
2)若第N步的状态之前走过,此时认为V_N=V
往前回溯的过程中G=r+gamma*V_N
![]()
这里面的V(St+1)就是V_N
持续更新中~