Treap图文详解、效率分析与拓展应用——清华大学计算机系 郭家宝
先给出我自己的一份Treap的代码——传送门
一、什么是 Treap
T r e a p = T r e e + H e a p Treap=Tree+Heap Treap=Tree+Heap
T
r
e
a
p
Treap
Treap是一种平衡树
T
r
e
a
p
Treap
Treap发音为[tri:p]
这个单词的构造选取了
T
r
e
e
Tree
Tree(树)的前两个字符和
H
e
a
p
Heap
Heap(堆)的后三个字符,
T
r
e
a
p
=
T
r
e
e
+
H
e
a
p
Treap=Tree+Heap
Treap=Tree+Heap
顾名思义
T
r
e
a
p
Treap
Treap把
B
S
T
BST
BST和
H
e
a
p
Heap
Heap结合了起来
它和
B
S
T
BST
BST一样满足许多优美的性质
而引入堆目的就是为了维护平衡。
T
r
e
a
p
Treap
Treap在
B
S
T
BST
BST的基础上添加了一个修正值
在满足
B
S
T
BST
BST性质的基础上
T
r
e
a
p
Treap
Treap节点的修正值还满足最小堆性质
最小堆性质可以被描述为每个子树根节点都小于等于其子节点
于是,
T
r
e
a
p
Treap
Treap可以定义为有以下性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值,而且它的根节点的修正值小于等于左子树根节点的修正值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值,而且它的根节点的修正值小于等于右子树根节点的修正值;
- 它的左、右子树也分别为 T r e a p Treap Treap。
图
5
5
5为一个
T
r
e
a
p
Treap
Treap
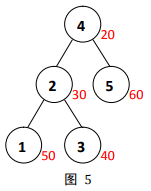
修正值是节点在插入到
T
r
e
a
p
Treap
Treap中时随机生成的一个值
它与节点的值无关
下述代码给出了
T
r
e
a
p
Treap
Treap的一般定义。
struct Treap_Node {
Treap_Node *left, *right; //节点的左右子树的指针
int value, fix; //节点的值和修正值
};
修正值全部满足最大堆性质也是可以的,在本文的介绍中,修正值全部是满足最小堆性质的。
为什么平衡
我们发现,
B
S
T
BST
BST会遇到不平衡的原因是因为有序的数据会使查找的路径退化成链
而随机的数据使
B
S
T
BST
BST退化的概率是非常小的
在
T
r
e
a
p
Treap
Treap中,修正值的引入恰恰是使树的结构不仅仅取决于节点的值,还取决于修正值的值
然而修正值的值是随机生成的
出现有序的随机序列是小概率事件
所以
T
r
e
a
p
Treap
Treap的结构是趋向于随机平衡的。
二、如何构建 Treap
旋转
为了使
T
r
e
a
p
Treap
Treap中的节点同时满足
B
S
T
BST
BST性质和最小堆性质
不可避免地要对其结构进行调整
调整方式被称为旋转
在维护
T
r
e
a
p
Treap
Treap的过程中,只有两种旋转
分别是左旋转(简称左旋)和右旋转(简称右旋)
旋转是相对于子树而言的
左旋和右旋的命名体现了旋转的一条性质:
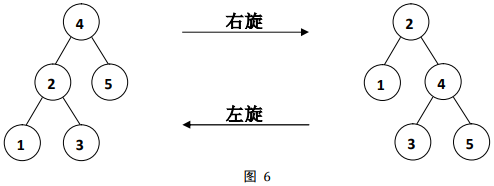
旋转的性质1
左旋一个子树,会把它的根节点旋转到根的左子树位置,同时根节点的右子节点成为子树的根
右旋一个子树,会把它的根节点旋转到根的右子树位置,同时根节点的左子节点成为子树的根
如图
6
6
6所示,我们可以从图中清晰地看出左旋后的根节点降到了左子树,右旋后根节点降到了右子树
而且仍然满足
B
S
T
BST
BST性质,于是有:
旋转的性质2
对子树旋转后,子树仍然满足
B
S
T
BST
BST性质。
利用旋转的两条重要性质
我们可以来改变树的结构
实际上我们恰恰是通过旋转使
T
r
e
a
p
Treap
Treap节点之间满足堆序。
如图
7
7
7所示的左边的一个
T
r
e
a
p
Treap
Treap,它仍然满足
B
S
T
BST
BST性质,但是由于某些原因,节点
4
4
4和节点
2
2
2之间不满足最小堆序,
4
4
4作为
2
2
2的父节点,它的修正值大于左子节点的修正值
我们只有将
2
2
2变成
4
4
4的父节点,才能维护堆序
根据旋转的性质我们可以知道,由于
2
2
2是
4
4
4的左子节点,为了使
2
2
2成为
4
4
4的父节点,我们需要把以
4
4
4为根的子树右旋
右旋后,
2
2
2成为了
4
4
4的父节点,满足堆序。
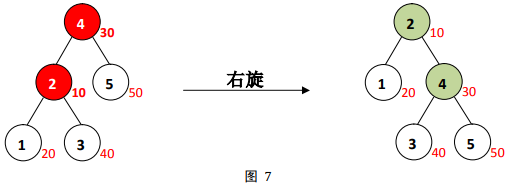
由此我们可以总结出,旋转的意义在于:
旋转可以使不满足堆序的两个节点通过调整位置,重新满足堆序,而不改变
B
S
T
BST
BST性质。
下述代码给出了两种旋转的实现。
void Treap_Left_Rotate(Treap_Node *&a) {//左旋 节点指针一定要传递引用
Treap_Node *b = a->right;
a->right = b->left;
b->left = a;
a = b;
}
void Treap_Right_Rotate(Treap_Node *&a) {//右旋 节点指针一定要传递引用
Treap_Node *b = a->left;
a->left = b->right;
b->right = a;
a = b;
}
遍历和查找
像大多数平衡树一样
在
T
r
e
a
p
Treap
Treap中查找和遍历不会改变
T
r
e
a
p
Treap
Treap的结构
所以在
T
r
e
a
p
Treap
Treap中查找和遍历的方法与基本的二叉查找树完全相同
具体方法参见二叉查找树
插入
在
T
r
e
a
p
Treap
Treap中插入元素与在
B
S
T
BST
BST中插入方法相似
首先找到合适的插入位置
然后建立新的节点,存储元素
但是要注意建立新的节点的过程中
会随机地生成一个修正值
这个值可能会破坏堆序
因此我们要根据需要进行恰当的旋转
具体方法如下:
- 从根节点开始插入;
- 如果要插入的值小于等于当前节点的值,在当前节点的左子树中插入,插入后如果左子节点的修正值小于当前节点的修正值,对当前节点进行右旋;
- 如果要插入的值大于当前节点的值,在当前节点的右子树中插入,插入后如果右子节点的修正值小于当前节点的修正值,对当前节点进行左旋;
- 如果当前节点为空节点,在此建立新的节点,该节点的值为要插入的值,左右子树为空,插入成功。
举例说明
如图
8
8
8,在已知的
T
r
e
a
p
Treap
Treap中插入值为
4
4
4的元素
找到插入的位置后,随机生成的修正值为
15
15
15。
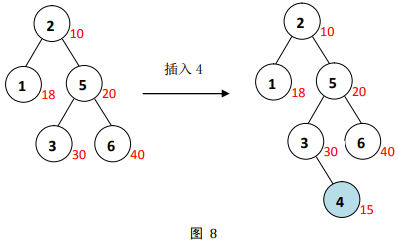
新建的节点
4
4
4与他的父节点
3
3
3之间不满足堆序
对以节点
3
3
3为根的子树左旋,如图
9
9
9。
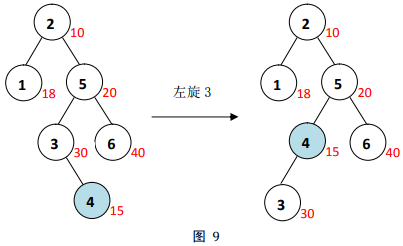
节点
4
4
4与其父节点
5
5
5仍不满足最小堆序
对以节点
5
5
5为根的子树右旋,如图
10
10
10
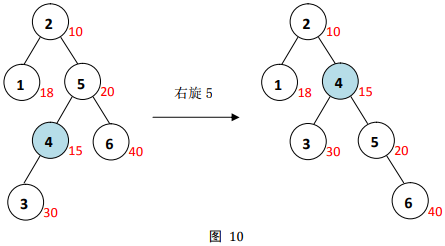
至此,节点
4
4
4与其父亲
2
2
2满足堆序,调整结束。
在
T
r
e
a
p
Treap
Treap中插入元素的期望时间是
O
(
l
o
g
N
)
O(logN)
O(logN)
下述代码为在
T
r
e
a
p
Treap
Treap中插入一个值为
7
7
7的元素。
Treap_Node *root;
void Treap_Insert(Treap_Node *&P, int value) {//节点指针一定要传递引用
if (!P) {//找到位置,建立节点
P = new Treap_Node;
P->value = value;
P->fix=rand();//生成随机的修正值
}
else if (value <= P->value) {
Treap_Insert(P->left, value);
if (P->left->fix < P->fix)
Treap_Right_Rotate(P);//左子节点修正值小于当前节点修正值,右旋当前节点
}
else {
Treap_Insert(P->right, value);
if (P->right->fix < P->fix)
Treap_Left_Rotate(P);//右子节点修正值小于当前节点修正值,左旋当前节点
}
}
int main() {
Treap_Insert(root, 7);//在 Treap 中插入值为 7 的元素
return 0;
}
删除
与
B
S
T
BST
BST一样,在
T
r
e
a
p
Treap
Treap中删除元素要考虑多种情况
我们可以按照在
B
S
T
BST
BST中删除元素同样的方法来删除
T
r
e
a
p
Treap
Treap中的元素
即用它的后继(或前驱)节点的值代替它,然后删除它的后继(或前驱)节点
为了不使
T
r
e
a
p
Treap
Treap向一边偏沉
我们需要随机地选取是用后继还是前驱代替它
并保证两种选择的概率均等
上述方法期望时间复杂度为
O
(
l
o
g
N
)
O(logN)
O(logN)
但是这种方法并没有充分利用
T
r
e
a
p
Treap
Treap已有的随机性质
而是重新得随机选取代替节点
我们给出一种更为通用的删除方法,这种方法是基于旋转调整的
首先要在
T
r
e
a
p
Treap
Treap树中找到待删除节点的位置,然后分情况讨论:
情况一,该节点为叶节点或链节点,则该节点是可以直接删除的节点
若该节点有非空子节点,用非空子节点代替该节点的,否则用空节点代替该节点,然后删除该节点。
情况二,该节点有两个非空子节点
我们的策略是通过旋转,使该节点变为可以直接删除的节点。如果该节点的左子节点的修正值小于右子节点的修正值,右旋该节点,使该节点降为右子树的根节点,然后访问右子树的根节点,继续讨论;反之,左旋该节点,使该节点降为左子树根节点,然后访问左子树的根节点,继续讨论,知道变成可以直接删除的节点。
下面给一个删除例子:在
T
r
e
a
p
Treap
Treap中删除值为
6
6
6的元素
如图
11
11
11,首先在
T
r
e
a
p
Treap
Treap中找到
6
6
6的位置
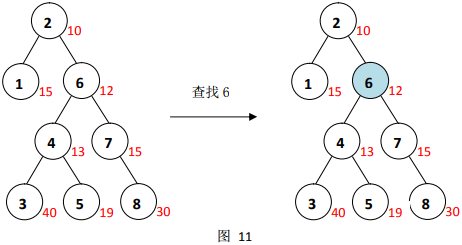
发现节点
6
6
6有两个子节点,且左子节点的修正值小于右子节点的修正值,需要右旋节点
6
6
6,如图
12
12
12。
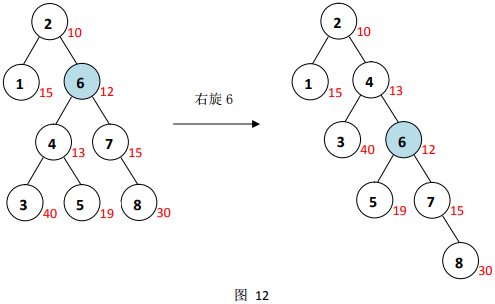
旋转后,节点
6
6
6仍有两个节点,右子节点修正值较小,于是左旋节点
6
6
6,如图
13
13
13。
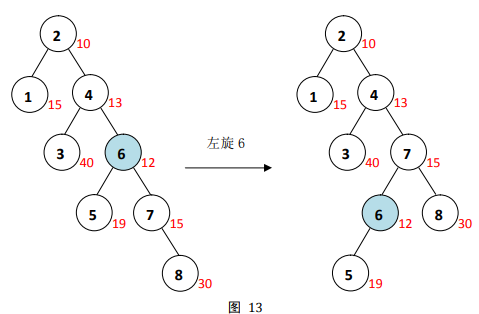
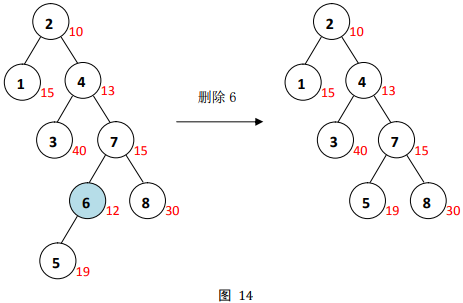
此时,节点
6
6
6只有一个子节点,可以直接删除,用它的左子节点代替它,删除本身,如图
14
14
14。
删除的复杂度稍高,但是期望时间仍为
O
(
l
o
g
N
)
O(logN)
O(logN)
但是在程序中更容易实现
下述代码给出了后一种(即上述图例中)的删除方法
在给定的
T
r
e
a
p
Treap
Treap中删除值为
6
6
6的节点。
BST_Node *root;
void Treap_Delete(Treap_Node *&P, int value) {//节点指针要传递引用
if (value == P->value) {//找到要删除的节点 对其删除
if (!P->right or !P->left) {//情况一,该节点可以直接被删除
Treap_Node *t = P;
if (!P->right) P = P->left; //用左子节点代替它
else P = P->right; //用右子节点代替它
delete t; //删除该节点
}
else {//情况二
if (P->left->fix < P->right->fix) {//左子节点修正值较小,右旋
Treap_Right_Rotate(P);
Treap_Delete(P->right, value);
}
else {//左子节点修正值较小,左旋
Treap_Left_Rotate(P);
Treap_Delete(P->left, value);
}
}
}
else if (value < P->value) Treap_Delete(P->left, value); //在左子树查找要删除的节点
else Treap_Delete(P->right, value); //在右子树查找要删除的节点
}
int main() {
Treap_Delete(root, 6);//在Treap中删除值为6的元素
return 0;
}
三、为什么要用 Treap
T r e a p Treap Treap的特点
-
T
r
e
a
p
Treap
Treap简明易懂
T r e a p Treap Treap只有两种调整方式,左旋和右旋
而且即使没有严密的数学证明和分析
T r e a p Treap Treap的构造方法,平衡原理也是不难理解的
只要能够理解 B S T BST BST和堆的思想,理解Treap当然不在话下 -
T
r
e
a
p
Treap
Treap易于编写
T r e a p Treap Treap只需维护一个满足堆序的修正值,修正值一经生成无需修改
相比较其他各种平衡树, T r e a p Treap Treap拥有最少的调整方式,仅仅两种相互对称的旋转
所以 T r e a p Treap Treap当之无愧是最易于编码调试的一种平衡树 -
T
r
e
a
p
Treap
Treap稳定性佳
T r e a p Treap Treap的平衡性虽不如 A V L AVL AVL、红黑树、 S B T SBT SBT等平衡树
但是 T r e a p Treap Treap也不会退化,可以保证期望 O ( l o g N ) O(logN) O(logN)的深度
T r e a p Treap Treap的稳定性取决于随机数发生器 -
T
r
e
a
p
Treap
Treap具有严密的数学证明
T r e a p Treap Treap期望 O ( l o g N ) O(logN) O(logN)的深度,是有严密的数学证明的
但这不是本文介绍的重点,大多略去 -
T
r
e
a
p
Treap
Treap具有良好的实践效果
各种实际应用中, T r e a p Treap Treap的稳定性表现得相当出色,没有因为任何的构造出的数据而退化
于是在信息学竞赛中,不少选手习惯于使用 T r e a p Treap Treap,均取得了不俗的表现。
T r e a p Treap Treap与其他平衡树的比较
与
B
S
T
BST
BST相比:
显而易见的,
B
S
T
BST
BST更加容易编程实现
对于完全随机的数据,
B
S
T
BST
BST会比
T
r
e
a
p
Treap
Treap更快,因为
B
S
T
BST
BST没有旋转等操作
但是在实际的应用中,往往会存在大量有序的数据,这时
B
S
T
BST
BST会退化,而
T
r
e
a
p
Treap
Treap仍旧能够保持随机的平衡。
与
S
p
l
a
y
Splay
Splay相比:
S
p
l
a
y
Splay
Splay和
B
S
T
BST
BST一样,不需要维护任何附加域,比
T
r
e
a
p
Treap
Treap在空间上有节约
S
p
l
a
y
Splay
Splay伸展操作中要用到的旋转相对于
T
r
e
a
p
Treap
Treap要稍复杂,编程实现不如
T
r
e
a
p
Treap
Treap容易
而且
S
p
l
a
y
Splay
Splay在查找时也会调整结构,这使得
S
p
l
a
y
Splay
Splay灵活性稍有欠缺
S
p
l
a
y
Splay
Splay的查找插入删除等基本操作的时间复杂度为均摊
O
(
l
o
g
N
)
O(logN)
O(logN)而非期望
可以故意构造出使
S
p
l
a
y
Splay
Splay变得很慢的数据,这在信息学竞赛中是很不利的
S
p
l
a
y
Splay
Splay找到了一个时间、空间和编程效率上的平衡点。
与
A
V
L
AVL
AVL、红黑树相比:
A
V
L
AVL
AVL、红黑树的平衡性是严格的,稳定性表现得十分出色
与
T
r
e
a
p
Treap
Treap一样,它们都要维护附加的域(高度、颜色)来实现平衡
A
V
L
AVL
AVL和红黑树在调整的过程中,旋转都是均摊
O
(
1
)
O(1)
O(1)的,而
T
r
e
a
p
Treap
Treap要
O
(
l
o
g
N
)
O(logN)
O(logN)
与
T
r
e
a
p
Treap
Treap的随机修正值不同,它们维护的附加域要动态的调整,而
T
r
e
a
p
Treap
Treap的随机修正值一经生成不再改变,这一点使得灵活性不如
T
r
e
a
p
Treap
Treap
最重要的是,
A
V
L
AVL
AVL和红黑树都是时间效率很高的经典算法,在许多专业的应用领域(如
S
T
L
STL
STL)有着十分重要的地位。
然而
A
V
L
AVL
AVL和红黑树的编程实现的难度要比
T
r
e
a
p
Treap
Treap大得多,正是由于过于复杂的编程,使得它们在信息学竞赛中备受冷落。
与
S
B
T
SBT
SBT相比:
作为平衡树中的新秀,
S
B
T
SBT
SBT有着能与
A
V
L
AVL
AVL和红黑树相媲美的严格平衡性,而实现的难度却远小于
A
V
L
AVL
AVL和红黑树
S
B
T
SBT
SBT的平衡附加域是子树的大小,而非其他的“无用”的值
S
B
T
SBT
SBT十分简洁高效,灵活性也很优秀
编程实现的难度要稍大于
T
r
e
a
p
Treap
Treap
然而
S
B
T
SBT
SBT没有受到学术界重视,原因是因为它只是在
A
V
L
AVL
AVL的基础上进行常数级的优化,而并没有突破性的进展。
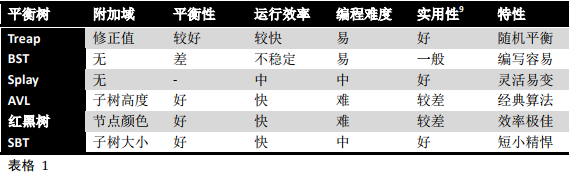
表格
1
1
1为几种平衡树的各种特性的对比。
四、Treap 的更多操作与技巧
查找、插入、删除是平衡树最基本的三种操作,但是在实际的应用中许多其他的操作都是必要的,而且 T r e a p Treap Treap这种强大的数据结构的功能远远不止此,下面我们要讨论的是 T r e a p Treap Treap更多的操作,以及一些技巧。
懒惰删除
基本的删除操作,比起插入和查找要稍有复杂
有时候,我们不愿意再写一段删除的程序代码,于是采用了懒惰删除(
l
a
z
y
lazy
lazy
d
e
l
e
t
i
o
n
deletion
deletion)的方法
懒惰删除就是在删除时,仅仅将元素找到后给元素打上“已被删除”的标记,而实际上不把它从平衡树中删除。
这种做法的优点是节约代码量,减少编程时间
但它的缺点也是很严重的:如果插入量和删除量都很大,这种删除方式会在平衡树中留下大量的“废节点”,浪费空间,还影响效率。
而且为了标记节点删除,我们还需要在节点定义中添加一个记录节点是否被删除的域
所以,只有在能够确定平衡树的吞吐量不是很大,或者不同数据的个数有限时,可以使用懒惰删除。
查找最值
在
B
S
T
BST
BST的删除中,我们需要通过找待删除节点的后继(或前驱),也就是其右子树的最大值(左子树的最小值)
在平衡树中查找最值也是经常会用到的一种操作,方法很简单。
查找一个子树的最小值,从子树的根开始访问,如果当前节点左子节点非空,访问当前节点的左子节点
如果当前节点左子节点已经为空,那么当前节点的值就是这个子树的最小值。
同理,查找一个子树的最大值,从子树的根开始访问,如果当前节点右子节点非空,访问当前节点的右子节点
如果当前节点右子节点已经为空,那么当前节点的值就是这个子树的最大值。
下述代码为在一个给定的
T
r
e
a
p
Treap
Treap中查找最大值和最小值的非递归实现
Treap_Node *root;
int Treap_FindMin(Treap_Node *P) {
while (P->left) P = P->left;//如果有左子节点,访问左子节点
return P->value;
}
int Treap_FindMax(Treap_Node *P) {
while (P->right) P = P->right;//如果有右子节点,访问右子节点
return P->value;
}
int main() {
int Min, Max;
Min = Treap_FindMin(root);//在 Treap 中查找最小值
Max = Treap_FindMax(root);//在 Treap 中查找最大值
return 0;
}
前驱与后继
求一个元素在平衡树(或子树)中的前驱,定义为查找该元素在平衡树中不大于该元素的最大元素
相似的,求一个元素在平衡树(或子树)中的后继,定义为查找该元素在平衡树中不小于该元素的最小元素。
从定义中看出,求一个元素在平衡树中的前驱和后继,这个元素不一定是平衡树中的值,而且如果这个元素就是平衡树中的值,那么它的前驱与后继一定是它本身
我们给出求前驱的基本思想:贪心逼近法
在树中查找,一旦遇到一个不大于这个元素的值的节点,更新当前的最优的节点,然后在当前节点的右子树中继续查找,目的是希望能找到一个更接近于这个元素的节点
如果遇到大于这个元素的值的节点,不更新最优值,在当前节点的左子树中继续查找
直到遇到空节点,查找结束,当前最优的节点的值就是要求的前驱
求后继的方法与上述相似,只是要找不小于这个元素的值的节点
下面是具体的算法描述。
求前驱:
- 从根节点开始访问,初始化最优节点为空节点;
- 如果当前节点的值不大于要求前驱的元素的值,更新最有节点为当前节点,访问当前节点的右子节点;
- 如果当前节点的值大于要求前驱的元素的值,访问当前节点的左子节点;
- 如果当前节点是空节点,查找结束,最优节点就是要求的前驱。
求后继:
- 从根节点开始访问,初始化最优节点为空节点;
- 如果当前节点的值不小于要求前驱的元素的值,更新最有节点为当前节点,访问当前节点的左子节点;
- 如果当前节点的值小于要求前驱的元素的值,访问当前节点的右子节点;
- 如果当前节点是空节点,查找结束,最优节点就是要求的后继。
在求前驱和后继的过程中,我们恰恰访问了从根到叶节点的一条完整的路径
由于
T
r
e
a
p
Treap
Treap的深度是
O
(
l
o
g
N
)
O(logN)
O(logN)的,所以求前驱和后继算法的时间复杂度为
O
(
l
o
g
N
)
O(logN)
O(logN)
下述代码为在一个已知的
T
r
e
a
p
Treap
Treap中求值为
5
5
5的元素前驱和后继
Treap_Node *root;
//访问节点 P,查找 value 的前驱,当前最优节点为 optimal
Treap_Node * Treap_pred(Treap_Node *P, int value, Treap_Node *optimal) {
if (!P) return optimal; //访问到空节点,返回最优节点,查找结束
if (P->value <= value) return Treap_pred(P->right, value, P); //更新最优值,在右子树中继续查找
else return Treap_pred(P->left, value, optimal); //左子树中继续查找
}
//访问节点 P,查找 value 的后继,当前最优节点为 optimal
Treap_Node * Treap_succ(Treap_Node *P, int value, Treap_Node *optimal) {
if (!P) return optimal; //访问到空节点,返回最优节点,查找结束
if (P->value >= value) return Treap_succ(P->left, value, P); //更新最优值,在左子树中继续查找
else return Treap_succ(P->right, value, optimal); //在右子树中继续查找
}
int main() {
Treap_Node *pred, *succ;
pred = Treap_pred(root, 5, 0); //查找 5 在 Treap 中的前驱
succ = Treap_succ(root, 5, 0); //查找 5 在 Treap 中的后继
return 0;
}
根据前驱和后继的定义,我们还可以以此来查找某个元素与
T
r
e
a
p
Treap
Treap中所有元素绝对值之差最小元素
如果按照数轴上的点来解释的话,就是求一个点的最近距离点
方法就是分别求出该元素的前驱和后继,比较前驱和后继哪个距离基准点最近。
求前驱、后继和距离最近点是许多算法中经常要用到的操作,
T
r
e
a
p
Treap
Treap都能够高效地实现。
合并重复节点
T
r
e
a
p
Treap
Treap中很可能存在值相同的节点,在某些特殊情况下,重复的节点可能会有很多,但是我们却把它们分别存成一个个节点
我们有一种常数级的优化,把重复的节点合并为一个节点
方法就是在
T
r
e
a
p
Treap
Treap节点中增加一个域,记录相同的这个值的个数,称为节点的权值,记为
w
e
i
g
h
t
weight
weight
在插入时,如果找到了已存在的相同的值,不必再开辟新的节点,只需把已有的节点的权值增加
1
1
1
删除时,只需把权值减少
1
1
1,如果权值为
0
0
0时,才对节点正式删除
这种优化的效果很好,首先是在插入时节省了开辟空间的时间
更好的是在删除时,避免了大量的旋转
当重复的值非常多的时候,这种优化是十分惊人的
下述代码为带重复计数的
T
r
e
a
p
Treap
Treap节点的定义
struct Treap_Node {
Treap_Node *left, *right; //节点的左右子树的指针
int value, fix, weight; //节点的值和修正值,weight 为权值
};
T r e a p Treap Treap中元素的类型与排序的规则
到这里为止,上文中提到的
T
r
e
a
p
Treap
Treap中元素的类型,我们都默认为了整数型
但实际上类型并没有限制,只要是能够比较大小的类型,例如浮点数型、字符串型,也可以是复合类型(结构类型、对象类型)
假若我们要实现一种多关键字类型排序的
T
r
e
a
p
Treap
Treap,我们只需自定义大于、小于、等于运算符的意义(运算符重载),使它们有确定的大小关系,这样就可以在不修改
T
r
e
a
p
Treap
Treap各种操作代码的基础上实现多关键字类型排序的
T
r
e
a
p
Treap
Treap
T
r
e
a
p
Treap
Treap定义中“左小于中小于右”,仅仅是逻辑上的定义,实际上我们可以以任何有序的规则排序,即使是左大于中大于右,只需要在比较元素大小的函数中修改定义即可
在以上时间复杂度的分析中,我们默认两个元素大小比较时间为
O
(
1
)
O(1)
O(1),但实际上某些复杂的类型间比较大小不是
O
(
1
)
O(1)
O(1)的,如字符串,是
O
(
L
)
O(L)
O(L),
L
L
L为字符串长度
平衡树并不适合作为所有数据类型的数据的有序存储容器,因为可能有些类型的两个元素直接相互比较大小是十分耗时的,这个常数时间的消耗是无法忍受的
例如字符串,作为检索字符串的容器,我们更推荐
T
r
i
e
Trie
Trie,而不是平衡树
平衡树仅适合做元素间相互比较时间很少的类型的有序存储容器。
维护子树大小的必要性
T
r
e
a
p
Treap
Treap是一种排序的数据结构,如果我们想查找第
k
k
k小的元素或者询问某个元素在
T
r
e
a
p
Treap
Treap中从小到大的排名时,我们就必须知道每个子树中节点的个数
我们称以一个子树的所有节点的权值之和,为子树的大小
由于插入、删除、旋转等操作,会使每个子树的大小改变,所以我们必须对子树的大小进行动态的维护。
对于旋转,我们要在旋转后对子节点和根节点分别重新计算其子树的大小。
对于插入,新建立的节点的子树大小为
1
1
1。在寻找插入的位置时,每经过一个节点,都要先使以它为根的子树的大小增加
1
1
1,再递归进入子树查找。
对于删除,在寻找待删除节点,递归返回时要把所有的经过的节点的子树的大小减少
1
1
1。要注意的是,删除之前一定要保证待删除节点存在于 Treap 中。
下述代码为维护子树大小的 T r e a p Treap Treap节点的定义,以及旋转
struct Treap_Node {
Treap_Node *left, *right; //节点的左右子树的指针
int value, fix, weight, size; //节点的值,修正值,重复计数,子树大小
inline int lsize() {return left ? left->size ? 0; } //返回左子树的节点个数
inline int rsize() {return right ? right->size ? 0; } //返回右子树的节点个数
};
void Treap_Left_Rotate(Treap_Node *&a) {//左旋 节点指针一定要传递引用
Treap_Node *b = a->right;
a->right = b->left;
b->left = a;
a = b;
b = a->left;
b->size = b->lsize() + b->rsize() + b->weight;
a->size = a->lsize() + a->rsize() + a->weight;
}
void Treap_Right_Rotate(Treap_Node *&a) {//右旋 节点指针一定要传递引用
Treap_Node *b = a->left;
a->size = b->rsize() + a->rsize() + a->weight;
b->size = b->lsize() + a->size + b->weight;
a->left = b->right;
b->right = a;
a = b;
b = a->left;
b->size = b->lsize() + b->rsize() + b->weight;
a->size = a->lsize() + a->rsize() + a->weight;
}
查找排名第k的元素
只有当我们维护以每个节点为根的子树的大小,才能查找排名第
k
k
k的元素
根据
T
r
e
a
p
Treap
Treap的一个重要性质,
T
r
e
a
p
Treap
Treap的子树也是
T
r
e
a
p
Treap
Treap,我们可以用分而治之的思想来查找排名第
k
k
k的元素
首先,在一个子树中,根节点的排名取决于其左子树的大小,如果根节点有权值
w
e
i
g
h
t
weight
weight,则根节点
P
P
P的排名是一个闭区间
A
A
A,且
A
=
[
P
.
l
e
f
t
.
s
i
z
e
+
1
,
P
.
l
e
f
t
.
s
i
z
e
+
P
.
w
e
i
g
h
t
]
A=[P.left.size+1,P.left.size+P.weight]
A=[P.left.size+1,P.left.size+P.weight]
根据此,我们可以知道,如果查找排名第
k
k
k的元素,
k
∈
A
k∈A
k∈A,则要查找的元素就是
P
P
P所包含元素
如果
k
<
A
k<A
k<A,那么排名第
k
k
k的元素一定在左子树中,且它还一定是左子树的排名第
k
k
k的元素
如果
k
>
A
k>A
k>A,则排名第
k
k
k的元素一定在右子树中,是右子树排名第
k
−
(
P
.
l
e
f
t
.
s
i
z
e
+
P
.
w
e
i
g
h
t
)
k-(P.left.size+P.weight)
k−(P.left.size+P.weight)的元素
根据这种策略,我们可以总结出算法
12
12
12:
- 定义 P P P为当前访问的节点,从根节点开始访问,查找排名第 k k k的元素;
- 若满足 P . l e f t . s i z e + 1 < = k < = P . l e f t . s i z e + P . w e i g h t P.left.size+1<=k<=P.left.size+P.weight P.left.size+1<=k<=P.left.size+P.weight,则当前节点包含的元素就是排名第 k k k的元素;
- 若满足 k < P . l e f t . s i z e + 1 k<P.left.size+1 k<P.left.size+1,则在左子树中查找排名第 k k k的元素;
- 若满足 k > P . l e f t . s i z e + P . w e i g h t k>P.left.size+P.weight k>P.left.size+P.weight,则在右子树中查找排名第 k − ( P . l e f t . s i z e + P . w e i g h t ) k-(P.left.size+P.weight) k−(P.left.size+P.weight)的元素。
下述代码为在一个给定的 T r e a p Treap Treap中查找排名第 8 8 8的元素。
Treap_Node *root;
Treap_Node * Treap_Findkth(Treap_Node *P, int k) {
if (k < P.lsize() + 1) //左子树中查找排名第 k 的元素
return Treap_Findkth(P->left, k);
else if (k > P.lsize() + P.weight) //在右子树中查找排名第 k-(P.lsize() + P.weight)的元素
return Treap_Findkth(P->right, k - (P.lsize() + P.weight));
else return P; //返回当前节点
}
int main() {
Treap_Node *result;
result = Treap_Findkth(root, 8); //在 Treap 中查找排名第 8 的元素
return 0;
}
根据上述算法,我们还可以实现查找逻辑第
k
k
k大元素,即查找第
(
r
o
o
t
.
s
i
z
e
−
k
+
1
)
(root.size-k+1)
(root.size−k+1)小元素,
r
o
o
t
.
s
i
z
e
root.size
root.size为整个
T
r
e
a
p
Treap
Treap的大小
甚至我们可以取代专门写的查找最值的算法
由于查找路径必定是一条子树上的路径,长度不会超过
T
r
e
a
p
Treap
Treap的深度,所以时间复杂度为
O
(
l
o
g
N
)
O(logN)
O(logN)。
求元素的排名
我们通过排名可以找到对应元素,也希望求出元素在
T
r
e
a
p
Treap
Treap中排名,或者成为求元素的秩
我们规定,如果在
T
r
e
a
p
Treap
Treap中有多个重复的元素,则这个元素的排名为最小的排名
例如
1
,
2
,
4
,
4
,
4
,
6
1,2,4,4,4,6
1,2,4,4,4,6中,
4
4
4的排名为
3
3
3
在
T
r
e
a
p
Treap
Treap中求元素的排名的方法与查找第
k
k
k小的数是很相似的,可以近似认为是互为逆运算。
我们的基本思想是查找要求的元素在
T
r
e
a
p
Treap
Treap中的位置,且在查找路径中统计出小于要求的元素的节点的总个数,要求的元素的排名就是总个数+
1
1
1
算法为:
- 定义 P P P为当前访问的节点, c u r cur cur为当前已知的比要求的元素小的元素个数。从根节点开始查找要求的元素,初始化 c u r cur cur为 0 0 0;
- 若要求的元素等于当前节点元素,要求的元素的排名为区间 [ P . l e f t . s i z e + c u r + 1 , P . l e f t . s i z e + c u r + w e i g h t ] [P.left.size+cur+1, P.left.size+cur+weight] [P.left.size+cur+1,P.left.size+cur+weight]内任意整数;
- 若要求的元素小于当前节点元素,在左子树中查找要求的元素的排名;
- 若要求的元素大于当前节点元素,更新 c u r cur cur为 c u r + P . l e f t . s i z e + w e i g h t cur+P.left.size+weight cur+P.left.size+weight,在右子树中查找要求的元素的排名。
下述代码为在一个已知的 T r e a p Treap Treap中求元素 8 8 8的排名。
Treap_Node *root;
int Treap_Rank(Treap_Node *P, int value, int cur) {//求元素 value 的排名
if (value == P->value) return P->lsize() + cur + 1; //返回元素的排名
else if (value < P->value) //在左子树中查找
return Treap_Rank(P->left, value, cur);
else //在右子树中查找
return Treap_Rank(P->right, value, cur + P->lsize() + weight);
}
int main() {
int rank;
rank = Treap_Rank(root, 8, 0); //在 Treap 中求元素 8 的排名
return 0;
}
维护附加关键字
有时候,我们建立 T r e a p Treap Treap维护的顺序关键字并不是我们主要关心的内容,而要关心的是附加关键字。根据不同目的维护的附加关键字的处理方法也不尽相同,下文仅仅以一个例子介绍附加关键字的处理方法。
顺序前缀和
[问题描述]
要求维护一个由二元组构成的序列,使序列中每个元素按第一关键字升序排列
操作包括:添加一个新元素,删除一个已有元素,查询这个序列的第二关键字最大前缀和
例如已知的序列
(
1
,
0
)
,
(
3
,
−
2
)
,
(
4
,
−
3
)
,
(
6
,
3
)
,
(
7
,
−
1
)
{(1,0), (3,-2), (4,-3), (6,3), (7,-1)}
(1,0),(3,−2),(4,−3),(6,3),(7,−1)
有如下几项操作:
添加
(
3
,
1
)
(3,1)
(3,1)入序列,添加
(
1
,
1
)
(1,1)
(1,1)入序列,从序列中删除
(
4
,
−
3
)
(4,-3)
(4,−3),查询最大前缀和
第
1
1
1次操作后,序列变成了
(
1
,
0
)
,
(
3
,
1
)
,
(
3
,
−
2
)
,
(
4
,
−
3
)
,
(
6
,
3
)
,
(
7
,
−
1
)
{(1,0), (3,1), (3,-2),(4,-3), (6,3), (7,-1)}
(1,0),(3,1),(3,−2),(4,−3),(6,3),(7,−1)
第
2
2
2次操作后,序列变成了
(
1
,
1
)
,
(
1
,
0
)
,
(
3
,
1
)
,
(
3
,
−
2
)
,
(
4
,
−
3
)
,
(
6
,
3
)
,
(
7
,
−
1
)
{(1,1), (1,0), (3,1), (3,-2), (4,-3), (6,3), (7,-1)}
(1,1),(1,0),(3,1),(3,−2),(4,−3),(6,3),(7,−1)
第
3
3
3次操作后,序列变成了
(
1
,
1
)
,
(
1
,
0
)
,
(
3
,
1
)
,
(
3
,
−
2
)
,
(
6
,
3
)
,
(
7
,
−
1
)
{(1,1), (1,0), (3,1), (3,-2), (6,3), (7,-1)}
(1,1),(1,0),(3,1),(3,−2),(6,3),(7,−1)
此时序列的 i 项前缀的和
S
[
i
]
=
1
,
1
,
2
,
0
,
3
,
2
S[i]={1,1, 2, 0, 3, 2}
S[i]=1,1,2,0,3,2
所以序列的最大前缀和是前
5
5
5项和,值为
3
3
3。
解析
由于序列总是要求升序排列,我们可以想到以元素第一关键字升序排列,使用
T
r
e
a
p
Treap
Treap维护。
由于每次要查询的是第二关键字构成的序列的最大前缀和,我们可以容易想到,对于第一关键字相同的元素,第二关键字大的元素应放在前面。
规定排序的顺序之后,我们要考虑如何维护前
i
i
i项元素的第二关键字的和(以下简称前 i 项的和)。设每个节点的第一关键字为
a
a
a,第二关键字为
b
b
b,我们要在
T
r
e
a
p
Treap
Treap中的节点添加附加域
s
u
m
sum
sum,表示以该节点为根的子树中所有元素的第二关键字和,以及附加域
m
a
x
max
max,表示以该节点为根的子树中所有元素构成的顺序序列最大的前缀和。
s
u
m
sum
sum值可以像维护子树的大小
s
i
z
e
size
size值一样的递归地维护,而且旋转时也要重新计算
而对于节点
p
p
p的
m
a
x
max
max值则要分情况讨论:
情况一,当前子树最大前缀的结尾在该节点的左子树,此时
p
.
m
a
x
=
p
.
l
e
f
t
.
m
a
x
p.max=p.left.max
p.max=p.left.max;
情况二,当前子树最大前缀的结尾恰好是该节点,此时
p
.
m
a
x
=
p
.
l
e
f
t
.
s
u
m
+
p
.
b
p.max=p.left.sum+p.b
p.max=p.left.sum+p.b;
情况三,当前子树最大前缀的结尾在该节点的右子树,
p
.
m
a
x
=
p
.
l
e
f
t
.
s
+
p
.
b
+
p
.
r
i
g
h
t
.
m
a
x
p.max=p.left.s+p.b+p.right.max
p.max=p.left.s+p.b+p.right.max。
在实际的插入和删除过程中,每次旋转后都要重新计算
s
u
m
sum
sum值,然后依次计算旋转后的子节点和根节点的
m
a
x
max
max值
维护好后,每次查询最大前缀和,只需要
O
(
1
)
O(1)
O(1)的时间。
时刻要记住
T
r
e
a
p
Treap
Treap是一种二叉树结构,它具有良好的分治结构,所以在维护各种具体的附加关键字时,二分或三分递推的思想一般都是解决问题的关键。