算法设计与分析——活动安排问题(Java)
【问题】设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源(如演讲会场),而在同一时间内只有一个活动能使用这一资源。每个活动 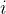 都有一个要求使用该资源的起始时间
都有一个要求使用该资源的起始时间 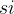 和一个结束时间
和一个结束时间 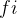 ,且
,且 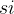 <
<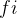 。如果选择了活动
。如果选择了活动 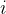 ,则它在半开时间区间 [
,则它在半开时间区间 [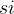 ,
,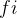 ) 内占用资源。若区间 [
) 内占用资源。若区间 [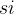 ,
,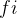 ) 与区间 [
) 与区间 [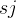 ,
,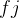 ) 不相交,则称活动
) 不相交,则称活动 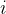 与活动
与活动 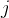 是相容的。也就是说,当
是相容的。也就是说,当 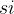 ≥
≥ 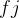 ,或
,或 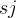 ≥
≥ 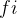 时,活动
时,活动 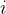 与活动
与活动 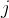 相容。活动安排问题(activity arrangement problem)要求在所给的活动集合中选出最大的相容活动子集。
相容。活动安排问题(activity arrangement problem)要求在所给的活动集合中选出最大的相容活动子集。
【想法】贪心法求解活动安排问题的关键是如何选择贪心策略,使得按照一定的顺序选择相容活动,并能够安排尽量多的活动。至少有以下两种看似合理的贪心策略。
(1)最早开始时间:这样可以增大资源的利用率。
(2)最早结束时间:这样可以使下一个活动尽早开始。
由于活动占用资源的时间没有限制,因此,后一种贪心选择更为合理。直观上,按这种策略选择相容活动可以为未安排的活动留下尽可能多的时间,也就是说,这种贪心选择的目的是使剩余时间段极大化,以便安排尽可能多的相容活动。
为了在每一次贪心选择时快速查找具有最早结束时间的相容活动,可以将 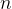 个活动按结束时间非减序排列。这样,贪心选择时取当前活动集合中结束时间最早的活动就归结为取当前活动集合中排在最前面的活动。
个活动按结束时间非减序排列。这样,贪心选择时取当前活动集合中结束时间最早的活动就归结为取当前活动集合中排在最前面的活动。
例如,设有11个活动等待安排,这些活动按结束时间的非减序排列如下表所示。
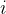 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
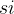 | 1 | 3 | 0 | 5 | 3 | 5 | 6 | 8 | 8 | 2 | 12 |
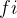 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
贪心法求解活动安排问题的过程如下图所示,其中阴影长条表示该活动已加入解集合中,空白长条表示该活动是当前正在检查相容性的活动。首先选择活动 1 加入解集合,因为活动 1 具有最早结束时间;活动 2 和活动 3 与活动 1 不相容,所以舍弃它们;活动 4 与活动 1 相容,因此将活动 4 加入解集合;然后在剩下的活动中找与活动 4 相容并具有最早结束时间的活动,依此类推。最终被选定的活动集合为{1,4,8,11}。 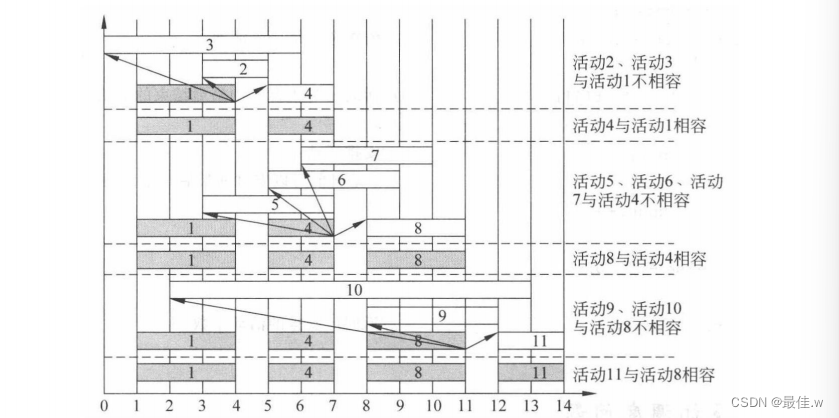
【算法】设有 n 个活动等待安排,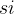 表示活动
表示活动 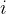 的起始时间,
的起始时间,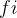 表示活动
表示活动 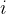 的结束时间( 1 ≤
的结束时间( 1 ≤ 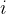 ≤
≤ 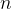 ),集合 B 存放问题的解,即选定的活动集合,算法如下。
),集合 B 存放问题的解,即选定的活动集合,算法如下。
输入: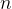 个活动的开始时间 {
个活动的开始时间 {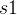 ,
,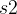 ,...,
,...,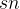 } 和结束时间 {
} 和结束时间 {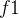 ,
,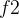 ,...,
,...,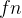 }
}
输出:选定的活动集合
1.对 {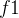 ,
,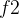 ,...,
,...,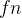 } 按非减序排序,同时相应地调整 {
} 按非减序排序,同时相应地调整 {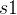 ,
,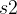 ,...,
,...,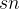 };
};
2.最优解中包含活动 1:B = {1};
3.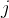 = 集合 B 中最后结束的活动,初始时
= 集合 B 中最后结束的活动,初始时 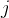 = 1;
= 1;
4.循环变量 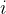 从 2~
从 2~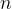 依次考察每一个活动:
依次考察每一个活动:
4.1 如果 ( 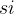 > =
> = 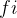 )则)
)则)
4.1.1 B=B 十 { 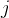 } ,
} ,
4.1.2 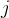 =
= 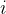 ;
;
4.2 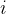 ++。
++。
【算法分析】在算法中,步骤 1 将各个活动按结束时间从小到大排序,其时间代价是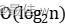 ;步骤 4 依次考察每一个活动,其时间代价是
;步骤 4 依次考察每一个活动,其时间代价是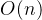 ,因此,算法的时间复杂性为
,因此,算法的时间复杂性为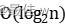 。
。
【算法实现】假设各活动的起始时间和结束时间存储在数组 s[ n ]和 f[ n ] 中且按结束时间非减序排列,数组 B[ n ] 存储活动的安排信息,若活动 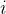 可以安排,则 B[ i ] = 1,注意数组下标从0开始,贪心法求解活动安排问题的算法用 JAVA 语言描述如下:
可以安排,则 B[ i ] = 1,注意数组下标从0开始,贪心法求解活动安排问题的算法用 JAVA 语言描述如下:
public class ActiveManage {
public static void main(String[] args) {
int n = 11;
int [] s = new int[]{1,3,0,5,3,5,6,8,8,2,12};
int [] f = new int[]{4,5,6,7,8,9,10,11,12,13,14};
int [] B =new int[n];
ActiveManage activeManage = new ActiveManage();
int k = activeManage.ActiveManage(s, f, B, n);
System.out.println("最多可安排的活动个数是:"+k);
System.out.println("具体的活动是:");
for (int i = 0; i < n; i++)
if (B[i] == 1)
System.out.println("活动"+i);
}
int ActiveManage(int s[ ], int f[ ], int B[ ], int n)
{
int i, j, count;
B[0] = 1; //安排活动1
j = 1; count = 1;
for (i = 1; i < n; i++) //依次考察每一个活动
{
if (s[i] >= f[j]) { //活动i与集合B中最后结束的活动j相容
B[i] = 1; //安排活动i
j = i; //j是目前可以安排的最后一个活动
count++;
}
else B[i] = 0;
}
return count; //返回已安排的活动个数
}
}
运行结果如下:
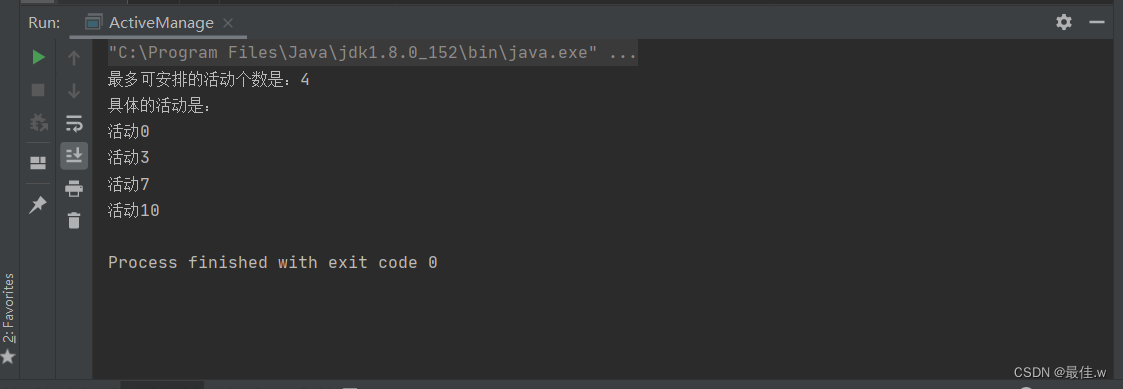
from:算法设计与分析(第2版)——王红梅 胡明 编著——清华大学出版社