选择排序——堆排序
一、堆排序的相关概念
1、堆的定义

从堆的定义可以看出,堆实质是满足如下性质的完全二叉树:二叉树中任一非叶子结点均小于(大于)它的孩子结点。
2、堆排序的定义
若在输出堆顶的最小值(最大值)后,使得剩余n- 1个元素的序列重又建成一个堆,则得到n个元素的次小值(次大值) ... .如此反复,便能得到一个有序序列,这个过程称之为堆排序。
二、堆的调整
1、如何在输出堆顶元素后,调整剩余元素为一个新的堆?
以小根堆为例:
①输出堆顶元素之后,以堆中最后一个元素替代之 ;
②然后将根结点值与左、右子树的根结点值进行比较,并与其中小者进行交换;
③重复上述操作②,直至叶子结点,将得到新的堆,称这个从堆顶至叶子的调整过程为"筛选"。
三、堆的建立
1、单结点的二叉树是堆;
2、在完全二叉树中所有以叶子结点(序号i > n/2)为根的子树是堆。这样,我们只需依次将以序号为n/2,n/2 - 1,......, 1的结点为根的子树均调整为堆即可。
即:对应由n个元素组成的无序序列,“筛选” 只需从第n/2个元素开始。
3、如下图所示是一个典例
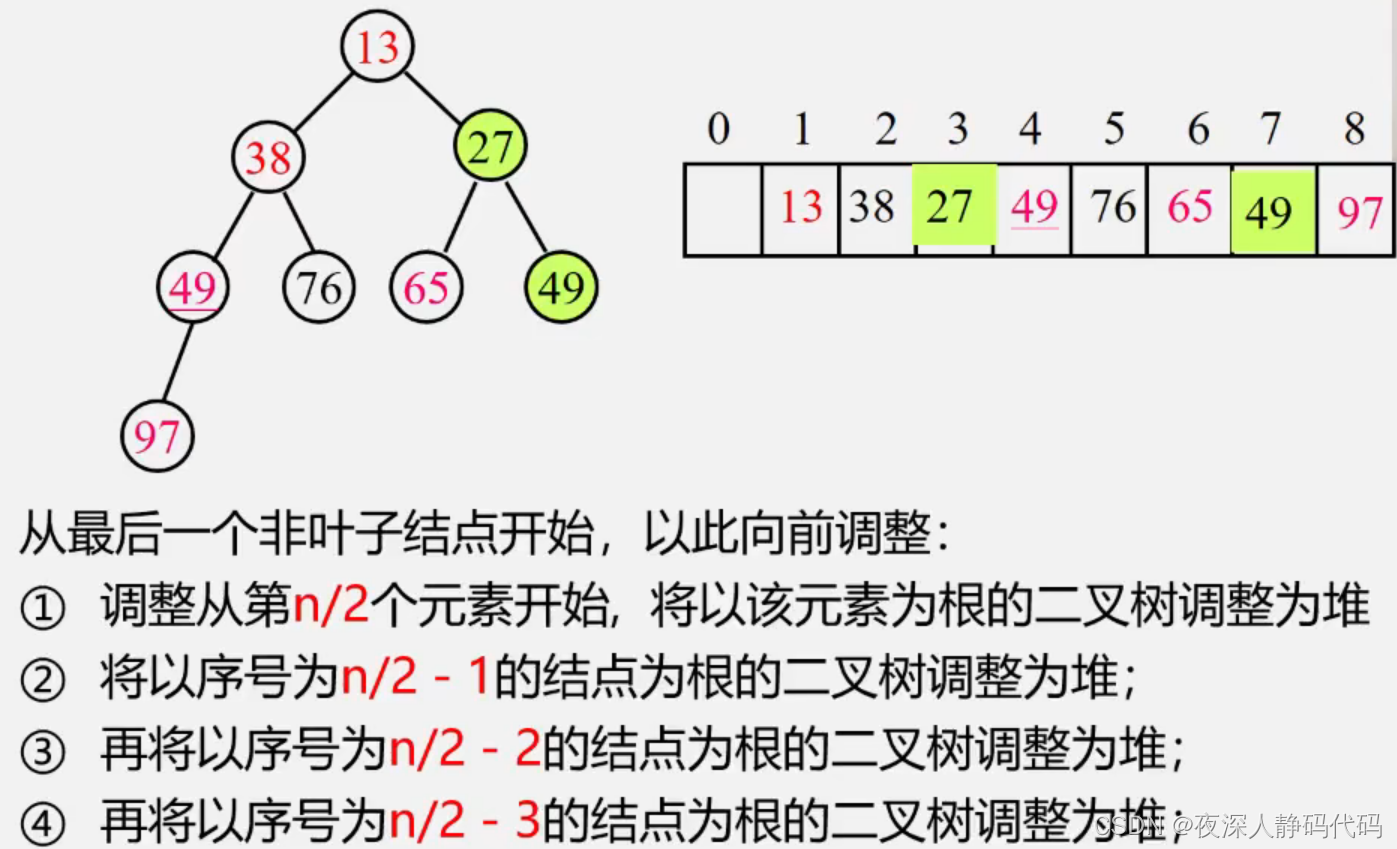
4、堆的建立过程其实就是堆排序过程。
四、堆的算法描述
void HeapSort( elem R[] ) { //对R[1 ]到R[n]进行堆排序
int i;
for (i= n/2; i >=1; i--)
HeapAdjust( R,i,n); //建初始堆
for (i= n; i>1; i--){ //进行n-1趟排序
Swap(R[1], R[i]); //根与最后一 个元素交换
HeapAdjust(R,1,i-1); //对R[1]到R[i -1]重新建堆
}
} //HeapSort
void HeapAdjust (elem R[ ], int S, int m) {
/*已知R[s..m]中记录的关键字除R[s]之外均满足堆的定义,本函数调整R[s]的关键字,使R[s..m]成为一个大根堆*/
rc = R[s];
for (j=2*s;j<=m;j*= 2){ //沿key较大的孩子结点向下筛选
if(j<m&&R[j] < R[j+1]) ++j; //j为key较大的记录的下标
if( rc >= R[j] ) break;
R[s] = R[j];S =j; // rc应插入在位置s上
}//for
R[s] = rc; //插入
} // HeapAdjust