张量操作与线性回归

一、张量的操作：拼接、切分、索引和变换

（1）张量拼接与切分

1.1 torch.cat()

功能：将张量按维度dim进行拼接
• tensors: 张量序列
• dim : 要拼接的维度
torch.cat(tensors, dim=0, out=None)函数用于沿着指定维度dim将多个张量拼接在一起。它接受一个张量列表tensors作为输入，并返回一个拼接后的张量。参数dim指定了拼接的维度，默认为0。

flag = True
if flag:
    t = torch.ones((2, 3)) #创建一个形状为(2, 3)的全为1的张量t

    t_0 = torch.cat([t, t], dim=0) # 将张量t沿着dim=0的维度拼接两次，得到张量t_0
    t_1 = torch.cat([t, t, t], dim=1)# 将张量t沿着dim=1的维度拼接三次，得到张量t_1

    print("t_0:{} shape:{}\nt_1:{} shape:{}".format(t_0, t_0.shape, t_1, t_1.shape))

t_0:tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]]) shape:torch.Size([4, 3])
t_1:tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.]]) shape:torch.Size([2, 9])

format()用于将t_0、t_0.shape、t_1和t_1.shape的值插入到字符串中的占位符位置。具体来说，{}是占位符，format()方法将会将对应的值填充到这些占位符的位置。
例如，“t_0:{} shape:{}\nt_1:{} shape:{}”.format(t_0, t_0.shape, t_1, t_1.shape)中的{}将会分别被t_0、t_0.shape、t_1和t_1.shape的值所替代。

1.2 torch.stack()

功能：在新创建的维度dim上进行拼接
• tensors:张量序列
• dim :要拼接的维度

torch.stack(tensors, dim=0, out=None)函数用于沿着指定维度dim将多个张量堆叠在一起。它接受一个张量列表tensors作为输入，并返回一个堆叠后的张量。参数dim指定了堆叠的维度，默认为0。

以下是示例代码：

import torch
# 示例张量
tensor1 = torch.tensor([1, 2, 3])
tensor2 = torch.tensor([4, 5, 6])
tensor3 = torch.tensor([7, 8, 9])
# 使用torch.cat()函数拼接张量
cat_result = torch.cat([tensor1, tensor2, tensor3], dim=0)
print("torch.cat()拼接结果：", cat_result)

# 使用torch.stack()函数堆叠张量
stack_result = torch.stack([tensor1, tensor2, tensor3], dim=0)
print("torch.stack()堆叠结果：", stack_result)

输出结果为：

torch.cat()拼接结果： tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])
torch.stack()堆叠结果： tensor([[1, 2, 3],
       						  [4, 5, 6],
       						  [7, 8, 9]])

1.3 torch.chunk()

torch.chunk()是PyTorch中的一个函数，用于将张量沿着指定维度进行分块。
函数的参数包括：

input：要分块的输入张量。
chunks：要分成的块数。
dim（可选）：指定要分块的维度，默认为0。
函数返回一个元组，包含分块后的张量块。
以下是一个示例代码：

import torch
x = torch.tensor([[1, 2, 3],
                  [4, 5, 6],
                  [7, 8, 9]])
chunks = torch.chunk(x, chunks=3, dim=0)
for chunk in chunks:
    print(chunk)

在上述代码中，我们创建了一个形状为(3, 3)的张量x。然后，我们使用torch.chunk()函数将x沿着dim=0的维度分成3块。
最后，我们使用for循环遍历每个分块，并打印出来。运行代码后，输出如下：

tensor([[1, 2, 3]])
tensor([[4, 5, 6]])
tensor([[7, 8, 9]])

可以看到，x被分成了3个块，每个块是一个形状为(1, 3)的张量。

1.4 torch.split()

torch.split()是PyTorch中的一个函数，用于将张量沿着指定维度进行切分。
函数的参数包括：

tensor：要切分的输入张量。
split_size_or_sections：切分的大小或切分的份数。当split_size_or_sections为整数时，表示每一份的长度；当split_size_or_sections为列表时，按照列表元素进行切分。
dim（可选）：指定要切分的维度，默认为0。
函数返回一个张量列表，包含切分后的张量。
以下是一个示例代码：

import torch
x = torch.tensor([[1, 2, 3, 4, 5],
                  [6, 7, 8, 9, 10],
                  [11, 12, 13, 14, 15]])
splits = torch.split(x, split_size_or_sections=2, dim=1)
for split in splits:
    print(split)

在上述代码中，我们创建了一个形状为(3, 5)的张量x。然后，我们使用torch.split()函数将x沿着dim=1的维度切分为大小为2的块。
最后，我们使用for循环遍历每个切分块，并打印出来。运行代码后，输出如下：

tensor([[ 1,  2],
        [ 6,  7],
        [11, 12]])
tensor([[ 3,  4],
        [ 8,  9],
        [13, 14]])
tensor([[ 5],
        [10],
        [15]])

可以看到，x被切分成了3个块，每个块的大小为(3, 2)、(3, 2)和(3, 1)。

（2）张量索引

2.1 torch.index_select()

torch.index_select()是PyTorch中的一个函数，用于按索引从输入张量中选择元素。
函数的参数包括：

input：输入张量。
dim：指定按哪个维度进行选择。
index：选择元素的索引。可以是一个张量或一个整数列表。
out（可选）：输出张量，用于存储结果。
函数返回一个新的张量，包含按索引选择的元素。
以下是一个示例代码：

import torch

# 创建一个输入张量
import torch

# 创建一个输入张量
x = torch.tensor([[1, 2, 3],
                  [4, 5, 6],
                  [7, 8, 9]])

# 创建一个索引张量
indices = torch.tensor([0, 2])

# 使用 torch.index_select() 函数按索引从输入张量中选择元素
selected = torch.index_select(x, dim=0, index=indices)

# 打印选择的结果
print(selected)

在上述代码中，我们创建了一个形状为(3, 3)的张量x。然后，我们使用torch.index_select()函数从x中按dim=0的维度选择索引为[0, 2]的元素。
最后，我们打印出选择的结果。运行代码后，输出如下：

tensor([[1, 2, 3],
        [7, 8, 9]])

可以看到，选择的结果是一个形状为(2, 3)的张量，其中包含了x中索引为0和2的两行。

2.2 torch.masked_select()

功能：按mask中的True进行索引
返回值：一维张量
• input: 要索引的张量
• mask: 与input同形状的布尔类型张量

import torch
# 创建一个输入张量
input = torch.tensor([[1, 2, 3],
                      [4, 5, 6],
                      [7, 8, 9]])
# 创建一个掩码张量
mask = torch.tensor([[1, 0, 1],
                     [0, 1, 0],
                     [1, 0, 1]], dtype=torch.bool)
# 使用 torch.masked_select() 函数根据掩码从输入张量中选择元素
output = torch.masked_select(input, mask)
print(output)

这段代码使用了 torch.masked_select() 函数，它的作用是根据掩码 mask 从输入张量 input 中选择元素。
在代码中，我们首先创建了一个形状为 (3, 3) 的输入张量 input。然后，我们创建了一个与输入张量形状相同的掩码张量 mask，其中的元素为布尔类型，用来指示要选择的元素。
接下来，我们调用 torch.masked_select() 函数，传入输入张量 input 和掩码张量 mask。函数会根据掩码选择对应位置为 True 的元素，并返回一个新的张量。
最后，我们将选择的结果存储在输出张量 output 中，并打印出来。运行代码后，输出如下：

tensor([1, 3, 5, 7, 9])

可以看到，输出张量 output 包含了输入张量 input 中掩码为 True 的元素。

（3）张量变换

3.1 torch.reshape()

功能：变换张量形状
注意事项：当张量在内存中是连续时，新张量与input共享数据内存
• input: 要变换的张量
• shape: 新张量的形状

import torch
# 创建一个输入张量
input = torch.tensor([[1, 2, 3],
                      [4, 5, 6]])
# 使用 torch.reshape() 函数改变张量的形状
output = torch.reshape(input, (3, 2))
print(output)

这段代码使用了 torch.reshape() 函数，它的作用是改变张量的形状。
在代码中，我们首先创建了一个形状为 (2, 3) 的输入张量 input。然后，我们调用 torch.reshape() 函数，传入输入张量 input 和目标形状 (3, 2)。
函数会将输入张量 input 改变为目标形状 (3, 2)，并返回一个新的张量。
最后，我们将改变形状后的结果存储在输出张量 output 中，并打印出来。运行代码后，输出如下：

tensor([[1, 2],
        [3, 4],
        [5, 6]])

可以看到，输出张量 output 的形状已经被改变为 (3, 2)，其中的元素顺序与输入张量 input 保持一致。

3.2 torch.transpose()

功能：交换张量的两个维度
• input: 要变换的张量
• dim0: 要交换的维度
• dim1: 要交换的维度

import torch
# 创建一个输入张量
input = torch.tensor([[1, 2, 3],
                      [4, 5, 6]])
# 使用 torch.transpose() 函数交换张量的维度
output = torch.transpose(input, 0, 1)
print(output)

这段代码使用了 torch.transpose() 函数，它的作用是交换张量的维度。
在代码中，我们首先创建了一个形状为 (2, 3) 的输入张量 input。然后，我们调用 torch.transpose() 函数，传入输入张量 input 和要交换的维度 dim0=0 和 dim1=1。
函数会将输入张量 input 的维度 0 和维度 1 进行交换，并返回一个新的张量。
最后，我们将交换维度后的结果存储在输出张量 output 中，并打印出来。运行代码后，输出如下：

tensor([[1, 4],
        [2, 5],
        [3, 6]])

可以看到，输出张量 output 的维度已经被交换，形状变为 (3, 2)，其中的元素顺序与输入张量 input 保持一致。

3.3 torch.t()

功能：2维张量转置，对矩阵而言，等价于 torch.transpose(input, 0, 1)

import torch
# 创建一个输入张量
input = torch.tensor([[1, 2, 3],
                      [4, 5, 6]])
# 使用 torch.t() 函数转置张量
output = torch.t(input)
print(output)

这段代码使用了 torch.t() 函数，它的作用是对张量进行转置操作。
在代码中，我们首先创建了一个形状为 (2, 3) 的输入张量 input。然后，我们调用 torch.t() 函数，传入输入张量 input。
函数会将输入张量 input 进行转置，并返回一个新的张量。
最后，我们将转置后的结果存储在输出张量 output 中，并打印出来。运行代码后，输出如下：

tensor([[1, 4],
        [2, 5],
        [3, 6]])

可以看到，输出张量 output 的维度已经被转置，形状变为 (3, 2)，其中的元素顺序与输入张量 input 保持一致

3.4 torch.squeeze()

功能：压缩长度为1的维度（轴）
• dim: 若为None，移除所有长度为1的轴；若指定维度，当且仅当该轴长度为1时，可以被移除；

import torch
# 创建一个输入张量
input = torch.tensor([[[1, 2, 3],
                       [4, 5, 6]]])
# 使用 torch.squeeze() 函数去除张量的尺寸为 1 的维度
output = torch.squeeze(input)
print(output)

这段代码使用了 torch.squeeze() 函数，它的作用是去除张量中尺寸为 1 的维度。
在代码中，我们首先创建了一个形状为 (1, 2, 3) 的输入张量 input。然后，我们调用 torch.squeeze() 函数，传入输入张量 input。
函数会去除输入张量 input 中尺寸为 1 的维度，并返回一个新的张量。
最后，我们将去除尺寸为 1 的维度后的结果存储在输出张量 output 中，并打印出来。运行代码后，输出如下：

tensor([[1, 2, 3],
        [4, 5, 6]])

可以看到，输出张量 output 的形状已经被修改，尺寸为 1 的维度被去除，变为 (2, 3)。

3.5 torchunsqueeze()

功能：依据dim扩展维度
• dim: 扩展的维度

抱歉，我之前给出的回答有误。在PyTorch中没有 torch.usqueeze() 函数。正确的函数是 torch.unsqueeze()，它的作用是在指定的维度上增加一个大小为1的维度。
以下是使用 torch.unsqueeze() 函数的示例代码：

import torch
# 创建一个输入张量
input = torch.tensor([[1, 2, 3],
                      [4, 5, 6]])
# 使用 torch.unsqueeze() 函数在维度0上增加一个大小为1的维度
output = torch.unsqueeze(input, dim=0)
print(output)

在这个示例中，我们创建了一个形状为 (2, 3) 的输入张量 input。然后，我们调用 torch.unsqueeze() 函数，传入输入张量 input 和要增加维度的维度索引 dim=0。
函数会在维度0上增加一个大小为1的维度，并返回一个新的张量。
最后，我们将增加维度后的结果存储在输出张量 output 中，并打印出来。运行代码后，输出如下：

tensor([[[1, 2, 3],
         [4, 5, 6]]])

可以看到，输出张量 output 的形状已经被修改，维度0上增加了一个大小为1的维度。

二、张量数学运算

一、加减乘除

torch.add(input, other, alpha=1)：将输入张量 input 和另一个张量 other 按元素相加，并返回结果张量。可选参数 alpha 控制相加的缩放因子。
torch.add() 功能：逐元素计算 input+alpha×other
• input: 第一个张量
• alpha: 乘项因子
• other: 第二个张量

torch.add(input, alpha=1, other, out=None) 是一个用于执行张量相加操作的函数。
参数说明：

input：输入张量。
alpha：一个可选的缩放因子，默认为1。它用于将 other 张量与 input 张量相乘后再相加。
other：另一个张量，与 input 张量进行相加操作。
out：可选的输出张量，用于存储结果。
函数功能：
该函数将输入张量 input 与另一个张量 other 进行按元素相加的操作，并返回结果张量。如果提供了 out 参数，结果将存储在 out 张量中；否则，将创建一个新的张量来存储结果。
请注意，input 和 other 的形状必须是可广播的，否则会引发错误。广播机制允许在不同形状的张量之间执行按元素操作。
示例用法：

import torch
input = torch.tensor([1, 2, 3])
other = torch.tensor([4, 5, 6])
result = torch.add(input, alpha=2, other=other)
print(result)  # 输出: tensor([9, 12, 15])

在这个示例中，input 张量为 [1, 2, 3]，other 张量为 [4, 5, 6]，alpha 参数为2。函数将 input 与 other 相乘得到 [2, 4, 6]，然后再与 other 相加得到结果 [6, 9, 12]。

torch.addcdiv(input, tensor1, tensor2, value=1)：将输入张量 input 与张量 tensor1 的按元素除法结果与张量 tensor2 相乘，然后加上一个标量值 value，并返回结果张量。

在这里插入图片描述

torch.addcmul(input, tensor1, tensor2, value=1)：将输入张量 input 与张量 tensor1 的按元素乘法结果与张量 tensor2 相加，然后加上一个标量值 value，并返回结果张量。

torch.addcmul(input, value=1, tensor1, tensor2, out=None) 是一个执行逐元素乘法和加法操作的函数。
参数说明：

input：输入张量。
value：一个可选的缩放因子，默认为1。它用于将 tensor1 与 tensor2 相乘后再与 input 相加。
tensor1：第一个张量，与 tensor2 相乘。
tensor2：第二个张量，与 tensor1 相乘。
out：可选的输出张量，用于存储结果。
函数功能：
该函数将输入张量 input 与 tensor1 和 tensor2 进行逐元素相乘，并将结果与 input 相加。如果提供了 out 参数，结果将存储在 out 张量中；否则，将创建一个新的张量来存储结果。
请注意，input、tensor1 和 tensor2 的形状必须是可广播的，否则会引发错误。广播机制允许在不同形状的张量之间执行按元素操作。
示例用法：

import torch
input = torch.tensor([1, 2, 3])
tensor1 = torch.tensor([4, 5, 6])
tensor2 = torch.tensor([2, 3, 4])
result = torch.addcmul(input, value=0.5, tensor1=tensor1, tensor2=tensor2)
print(result)  # 输出: tensor([5., 7.5, 10.])

在这个示例中，input 张量为 [1, 2, 3]，tensor1 张量为 [4, 5, 6]，tensor2 张量为 [2, 3, 4]，value 参数为0.5。函数将 tensor1 与 tensor2 逐元素相乘得到 [8, 15, 24]，然后再与 input 相加得到结果 [9, 17, 27]。

torch.sub(input, other)：将输入张量 input 和另一个张量 other 按元素相减，并返回结果张量。
torch.div(input, other)：将输入张量 input 和另一个张量 other 按元素相除，并返回结果张量。
torch.mul(input, other)：将输入张量 input 和另一个张量 other 按元素相乘，并返回结果张量。

二、对数，指数，幂函数

torch.log(input, out=None)：计算输入张量 input 的自然对数，并返回结果张量。
torch.log10(input, out=None)：计算输入张量 input 的以10为底的对数，并返回结果张量。
torch.log2(input, out=None)：计算输入张量 input 的以2为底的对数，并返回结果张量。
torch.exp(input, out=None)：计算输入张量 input 的指数函数，即 e^x，其中 e 是自然对数的底数，并返回结果张量。
torch.pow(input, exponent, out=None)：计算输入张量 input 的每个元素的指数幂，指数由参数 exponent 指定，并返回结果张量。

三、三角函数

torch.abs(input, out=None)：计算输入张量 input 的绝对值，并返回结果张量。
torch.acos(input, out=None)：计算输入张量 input 的反余弦值（弧度制），并返回结果张量。
torch.cosh(input, out=None)：计算输入张量 input 的双曲余弦值，并返回结果张量。
torch.cos(input, out=None)：计算输入张量 input 的余弦值（弧度制），并返回结果张量。
torch.asin(input, out=None)：计算输入张量 input 的反正弦值（弧度制），并返回结果张量。
torch.atan(input, out=None)：计算输入张量 input 的反正切值（弧度制），并返回结果张量。
torch.atan2(input, other, out=None)：计算输入张量 input 与另一个张量 other 的反正切值（弧度制），并返回结果张量。

三、线性回归

在这里插入图片描述

import torch
import matplotlib.pyplot as plt

# 设置随机种子
torch.manual_seed(10)

# 学习率
lr = 0.05

# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1)

# 构建线性回归参数
w = torch.randn((1), requires_grad=True)  # 权重 w，随机初始化
b = torch.zeros((1), requires_grad=True)  # 偏置 b，初始化为零

# 迭代训练
for iteration in range(1000):

    # 前向传播
    wx = torch.mul(w, x)  # wx = w * x
    y_pred = torch.add(wx, b)  # y_pred = wx + b

    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 反向传播
    loss.backward()

    # 更新参数
    b.data.sub_(lr * b.grad)  # 更新偏置 b
    w.data.sub_(lr * w.grad)  # 更新权重 w

    # 清零梯度
    w.grad.zero_()
    b.grad.zero_()

    # 绘图
    if iteration % 20 == 0:
        plt.cla()  # 清除当前图形
        plt.scatter(x.data.numpy(), y.data.numpy())  # 绘制训练数据的散点图
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)  # 绘制当前的拟合线
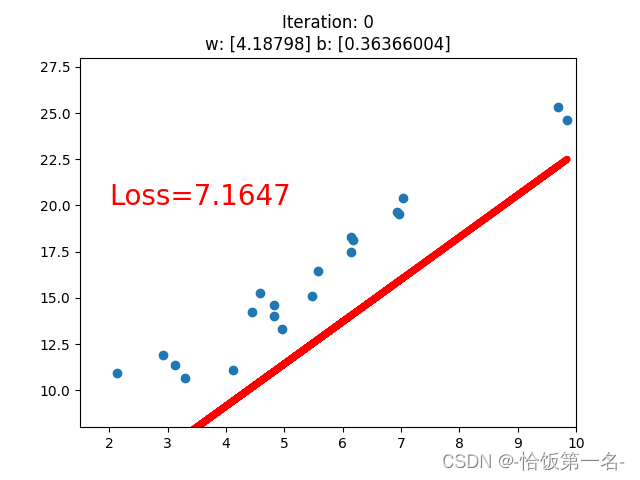
        plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})  # 显示当前的损失值
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))  # 显示当前的迭代次数和参数值
        plt.pause(0.5)

        if loss.data.numpy() < 1:
            break

plt.show()  # 显示图形

这段代码是一个简单的线性回归模型的训练过程，并且使用 matplotlib 库将训练过程可视化。

代码首先导入了 torch 和 matplotlib.pyplot 库，并设置了随机种子。
接下来，代码创建了训练数据，其中 x 是一个形状为 (20, 1) 的随机张量，y 是根据公式 2*x + (5 + 随机噪声) 生成的张量。
然后，代码定义了线性回归模型的参数 w 和 b，它们都是需要梯度计算的张量。

在每次迭代中，代码进行了以下操作：

前向传播：根据当前的 w 和 b 计算预测值 y_pred。
计算均方误差（MSE）损失函数。
反向传播：根据损失函数计算梯度。
更新参数：使用学习率 lr 和梯度更新参数 w 和 b。
清零梯度：使用 w.grad.zero_() 和 b.grad.zero_() 清零参数的梯度。

每隔 20 次迭代，代码会绘制训练数据的散点图，并在图中绘制当前的拟合线。同时，代码还会显示当前的损失值和参数 w、b 的数值。如果损失值小于 1，代码会提前结束训练。最后，通过 plt.show() 显示图形。