【Python实现杨辉三角】
目录
一、什么是杨辉三角
杨辉三角,是二项式系数在三角形中的一种几何排列,中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623----1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。

杨辉三角的性质:
每个数字等于上一行的左右两个数字之和。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和。
为了解决这个问题,并了解更多的解法,我在网上查找了一些资料,将解法进行了汇总
二、杨辉三角解法
1. 定义法
思路:
从第三行开始,每一行的首尾都是1,中间部分每个数字等于上一行的左右两个数字之和。先定义每一行的第一个数字,然后在利用规则对中间部分进行运算,最后再添加最后一个元素。
PS:这个解法还是比较容易想出来的
代码:
# 计算杨辉三角 定义法
n = eval(input("输入要打印的行数:"))
triangle = [[1], [1, 1]]
for i in range(2, n): # 已经给出前两行,求剩余行
pre = triangle[i-1] # 上一行
cul = [1] # 定义每行第一个元素
for j in range(i-1): # 算几次
cul.append(pre[j]+pre[j+1]) # 每个数字等于上一行的左右两个数字之和。
cul.append(1) # 添加每行最后一个元素
triangle.append(cul)
print("普通输出:{}".format(triangle))
for i in range(n): # 按等边三角形格式输出
s = " "*(n-i-1)
for j in triangle[i]:
s = s + str(j)+" "
print(s)运行结果
定义法也可以使用下面这种形式,先给出一个空列表,通过循环先进行追加列表,在对列表进行修改
代码
n = eval(input())
triangle = []
for i in range(n):
cur = [1]
triangle.append(cur) #先追加进去
if i == 0:
continue
pre = triangle[i-1]
for j in range(i-1):
cur.append(pre[j] + pre[j+1])
cur.append(1)
print(triangle)2. 补0法
补零法是在定义法的基础上,通过对上一行加[0],那么每行只需定义每行的第一个元素,这一行的其余元素可以通过上一行的左右两个元素相加得到。值得注意的是补零只是对中间的过程变量进行补零,不影响输出结果。
代码
# 计算杨辉三角 补0法
triangle = [[1]]
n = eval(input("输入行数:"))
for i in range(1, n):
swap = triangle[i-1]+[0]
cul = [1]
for j in range(len(swap)-1):
cul.append(swap[j]+swap[j+1])
triangle.append(cul)
print(triangle)
运行结果
3.对称法
思路
中点的确定: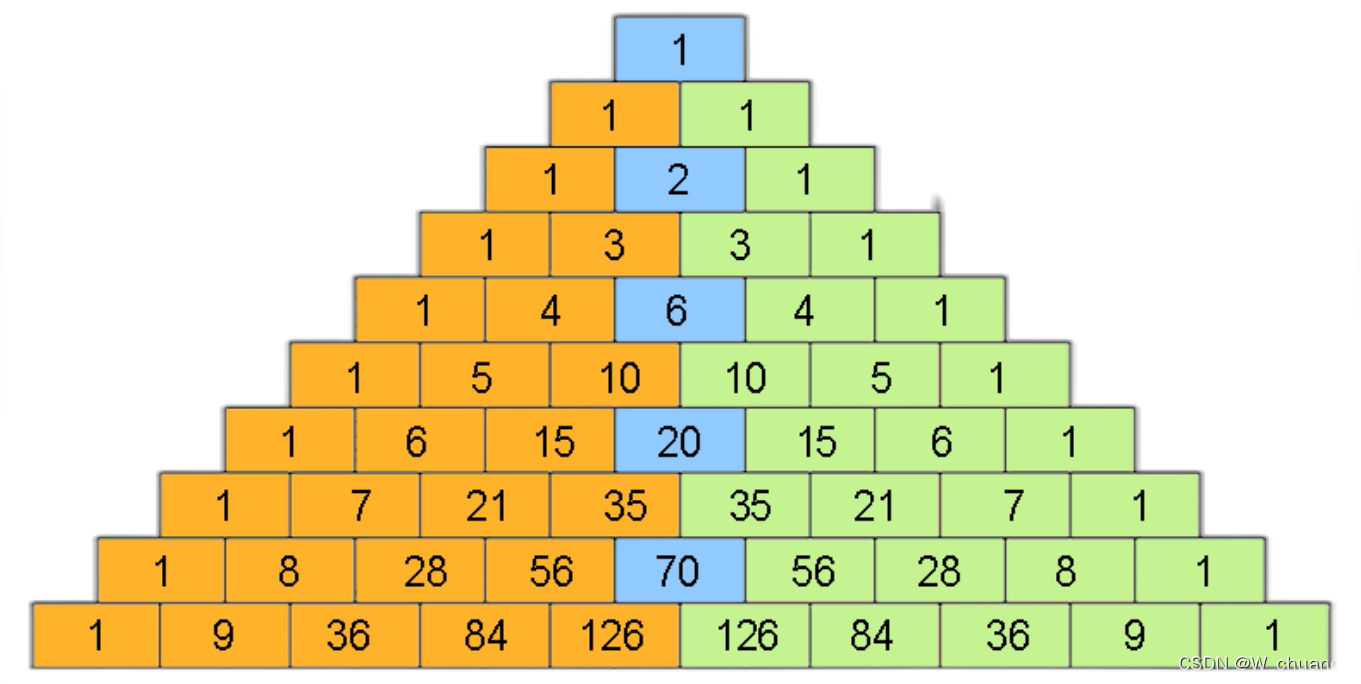
代码:
# 杨辉三角,对称法
n = eval(input("输入要打印的行数:"))
triangle = [[1], [1, 1]]
for i in range(2, n):
tmp = triangle[-1]#上一个列表
cul = [1] * (i+1)
for j in range(i//2): #有图知:大概的临界值为一半,再仔细推敲
cul[j+1] = tmp[j]+tmp[j+1]
if i != 2j:#当j不为中点时
cul[-j-2] = cul[j+1]
triangle.append(cul)
print(triangle)
运行结果
4. 杨辉三角,单列表方法
代码
# 杨辉三角,单列表解决
n = eval(input("输入要打印的行数:"))
row = [1] * n
for i in range(n):
z = 1
offset = n - i
for j in range(1, i//2+1):
val = z + row[j]
z = row[j]
row[j] = val
if i != 2*j:
row[-j - offset] = val
print(row[:i+1])
运行结果

5.列表嵌套(二维数组)
概念:list1[n][m] = list1[n-1][m-1] + list1[n-1][m]
代码
n=int(input())
list1=[]
for n in range(n):
row=[1] # 第一行第一列为1
list1.append(row)
if n==0:
for num in row: # 这里主要是为输出做的格式处理
print(num,end=" ")
print()
continue
for m in range(1,n):
row.append(list1[n-1][m-1]+list1[n-1][m])
row.append(1)
for num in row:
print(num, end=" ")
print()
这个方法利用List列表将二维数组进行实现
6. 新旧两行,一次性开辟新行
代码
m = eval(input("输入要输出的行数:"))
# 新旧两行,一次性开辟新行
ordline = []
for i in range(m):
newline = [1] * (i+1)
for j in range(2, i+1):
newline[j-1] = oldline[j-1]+oldline[j-2]
oldline = newline
print(newline)
运行结果
其中通过计算比较,第五种方法一次性开辟内存空间的方法要比第一种方法中,每次计算通过append添加新的内存空间要快。
7.yield函数
利用yield函数可以将L定义为生成器
代码
def triangles():
L = [1] #定义L为一个只包含一个元素的列表
while True:
yield L #定义为生成器函数
L =[1] + [L[n] + L[n-1] for n in range(1,len(L))] + [1]
n = 0
for t in triangles():
print(t)
n = n + 1
if n == 10:
break8.zip函数
zip() 函数用于将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
如果各个迭代器的元素个数不一致,则返回列表长度与最短的对象相同,利用 * 号操作符,可以将元组解压为列表。
思路
杨辉三角特性:


代码
def triangles():
n = [1]
while True:
yield n
n = [x+y for x,y in zip([0] + n,n+[0])]
n = 0
for t in triangles():
print(t)
n = n + 1
if n == 10:
break运行结果
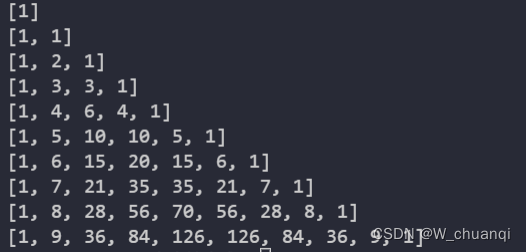
参考资料链接:
杨辉三角的几种解法(python)_vampire's blood的博客-CSDN博客_杨辉三角python