小敖同学在学数据结构

算法与数据结构

简单排序算法
二分法详解与扩展
对数器
递归行为和递归行为时间复杂度的估算master公式
- 归并排序
异或运算符 “∧”
哈希表

简单排序算法

void swap(int& m, int& n) {
	int temp = m;
	m = n;
	n = temp;
}

选择排序：每次选择无序序列中最小的值放入有序序列中

// 选择排序 i从0到n-1，将剩下元素中的最小值与i交换
void selectionSort(vector<int> &a) {
	int n = a.size();
	for (int i = 0; i < n-1; ++i) {
		int minIndex = i;
		for (int j = i + 1; j < n; ++j) { // 找到剩下元素中的最小值并得到索引
			minIndex = a[minIndex] < a[j] ? minIndex : j;
		}
		// 交换最小值元素和i位置元素
		swap(a[minIndex], a[i]);
	}
}

冒泡排序：比较相邻元素，将最大值冒泡到最右边O(N^2)

/* 冒泡排序 从左到右依次比较相邻两个元素大小，将更大的值交换到右边，直到末尾。
第一层for循环表示无序容器的范围 第二层for循环交换相邻元素*/
void bubbleSort(vector<int> &a) {
	int n = a.size();
	for (int i = n-1; i > 0; --i) {
		for (int j = 0; j < i; ++j) {
			if (a[j] > a[j + 1]) {
				swap(a[j], a[j + 1]);
			}
		}
	}
}

插入排序：类似于扑克牌插牌当前的数小于左边的数就往左交换，当往左换到最左边或者不小于左边数时停止交换。O(N^2)

// 插入排序 插入排序 将右边的无序列表中的数依次往左边的有序列表中逐个比较，若前面的数大于这个数，交换
void insertionSort(vector<int> &a) {
	// 默认0~0有序，0~i想有序
	for (int i = 1; i < a.size(); ++i) {
		for (int j = i; j > 0 && a[j - 1] > a[j]; --j) {
			swap(a[j - 1], a[j]);
		}
	}
}

希尔排序

1.选定一个增长量h，以增长量h作为分组的依据；
2.对分好组的每一组数据完成插入排序；
3.减小增长量，最少减为1，重复第二步操作。

void shellSort(vector<int>& a) {
	int h = 0;
	while (h < a.size() / 2 - 1) {
		h = 2 * h + 1;
	}
	while (h >= 1) {
		for (int i = h; i < a.size(); ++i) {
			for (int j = i; j >= h && a[j - h] > a[j]; j -= h) {
				swap(a[j - h], a[j]);
			}
		}
		h /= 2;
	}
}

希尔排序时间复杂度非常难以分析，它的平均复杂度界于 O(n) 到 O(n^2) 之间，普遍认为它最好的时间复杂度为 O(n^1.3)

快速排序

采用分治法来对数组进行排序。快速排序的基本思想是选择一个基准元素，然后将数组分割成两个子数组，其中一个子数组的元素都小于基准元素，另一个子数组的元素都大于基准元素。然后递归地对这两个子数组进行排序，最终得到有序的数组。

// 快速排序函数
void quickSort(std::vector<int>& arr, int left, int right) {
    if (left >= right) return;

    int pivot = arr[left]; // 选择第一个元素作为基准元素
    int low = left, high = right;

    while (low < high) {
        while (low < high && arr[high] >= pivot) high--; // 从右侧找到小于基准元素的元素
        while (low < high && arr[low] <= pivot) low++;   // 从左侧找到大于基准元素的元素
        if (low < high) swap(arr[low], arr[high]);       // 交换这两个元素
    }

    // 将基准元素放到正确的位置，此时low等于high
    arr[left] = arr[low];
    arr[low] = pivot;

    // 递归排序左右两个子数组
    quickSort(arr, left, low - 1);
    quickSort(arr, low + 1, right);
}

二分法详解与扩展

1）在一个有序数组中找某个数是否存在
时间复杂度O(logn)
2）在一个有序数组中，找>=某个数最左侧的位置
3）局部最小值问题
在一个无序数组a中，若a[0]<a[1]，认为局部最小值为a[0]；若a[n-1]<a[n-2]，局部最小值为a[n-1]；其他地方a[m]<a[m-1]且a[m]<a[m+1]，局部最小为a[m]。
在无序数组中也可以采用二分法，对于局部最小值问题，
首先对a[0]和a[1]进行比较，若满足a[0]<a[1]，则认为a[0]为局部最小，直接返回；
若不满足，再对a[n-1]和a[n-2]进行比较，若满足a[n-1]<a[n-2]，局部最小值为a[n-1]，直接返回；
若都不满足，观察两端数据变化趋势，就说明在a[0]和a[n-1]中间的某个位置一定存在局部最小值，采用二分法，若存在a[m]<a[m-1]且a[m]<a[m+1]，则局部最小为a[m]，若a[m]>a[m-1]，就往m-1方向继续二分，直到找到满足条件的位置后返回。
二分找局部最小

对数器

用两种方法对比的结果是否一致测试方法的正确性

递归行为和递归行为时间复杂度的估算master公式

在这里插入图片描述

例找数组中最大值：

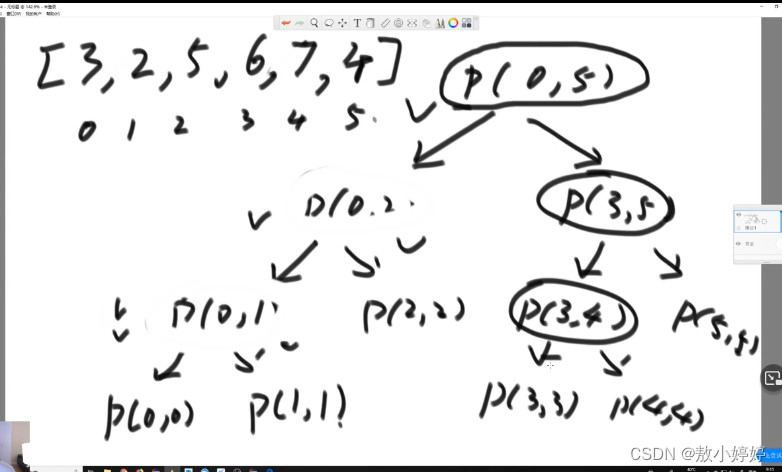
求最大值在这里插入图片描述

递归过程相当于构建了一颗多叉树，计算数的所有结点的过程就是利用栈进行了后序遍历，每一个结点都通过自己的子结点给自己汇总信息之后才能够继续往上返回，栈空间相当于整棵树的高度，只用在这个高度上压栈。

小知识点求数组中点写法：
mid=(L+R)/2：一般写法，但是当数组长度比较大，（L+R）可能会溢出，mid可能会算出负的下标，所以mid可以写成
mid=L+(R-L)/2：不会溢出，更简化写法是
mid=L+((R-L)>>1)：右移一位等于除二，而且右移一位比除二要快。

在这里插入图片描述 master公式的使用
T(N) = a*T(N/b) + O(N^d)
T(N)指母问题的数据量规模是N
T(N/b)子过程的规模是N/b
a指调用次数
O(N^d) 除了子过程之外剩下过程的规模（时间复杂度）。
求最大值

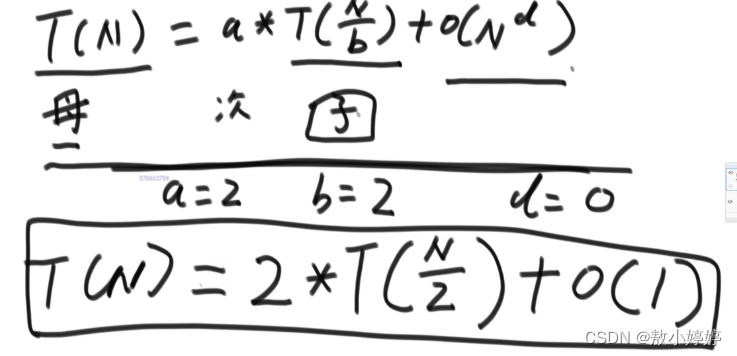
上面求数组最大值满足master公式，母问题数据量为数组长度，数组取中间将子问题划分为左边和右边，子问题数据量长度为N/2，分别调用两次，剩下过程规模为O(1)。
要满足master公式必须让子问题数据量规模一致！！！

在这里插入图片描述
此例中 a=2,b=2,d=0,log(b,a)=log(2,2)=1满足1），时间复杂度为O(N)

归并排序

/*归并排序，首先是一个递归过程，
将有序数组从中间分为左右两边，左指针和右指针一开始分别指向两边最左边的位置，
开辟一个新数组，比较左指针和右指针指向元素大小，更小的放入数组，并将该指针右移，直到有一个指针
到达边界，将另一个指针剩余元素放入数组，将原数组替换为该数组
*/
void Merge(std::vector<int>& a, int left, int mid, int right) {
	int l = left;
	int r = mid + 1;
	//std::vector<int> b;
	int* b = new int[right - left + 1];
	int i = 0;
	while (l <= mid && r <= right) {
		b[i++] =(a[l] < a[r] ? a[l++] : a[r++]);
	}
	while (l <= mid) {
		b[i++] = a[l++];
	}
	while (r <= right) {
		b[i++] = a[r++];
	}
	for (int m = 0; m < right - left + 1; ++m) {
		a[left + m] = b[m];
	}
	delete[] b;
}
void mergeSort(int left, int right, std::vector<int> &a) {
	if (left == right) {
		return;
	}
	int mid = (left + right)/2;
	mergeSort(left, mid, a);
	mergeSort(mid + 1, right, a);
	Merge(a, left, mid, right);
}

每一次的比较行为没有被浪费，时间复杂度O(N*logN)。每次new一个长度为N的动态数组，比较完后释放，因此额外空间复杂度O(N)。

归并排序扩展小和问题

异或运算符 “∧”

参考 c++异或运算以及力扣题
也称作XOR运算符相同为0，相异为1。 0∧0=0， 0∧1=1， 1∧0=1， 1∧1=0
特性：

与0异或，保留原值
与自己异或，结果为0
交换两个值

a = a^b;
b = a^b;
a = a^b;

力扣题

找出值为0到n中缺失的一个数 leetcode No268. Missing Number

For example,
Given nums = [0, 1, 3] return 2.
思路：定义一个数a，先把0到n全部与a异或，再把nums中的数全部与a异或，得到的结果就是缺失的数。

int missingNumber(vector<int>& nums) {
        int a=0;
        for(int i =1; i<= nums.size(); ++i) {
            a^=i;
        }
        for(int m : nums) {
            a^=m;
        }
        return a;
    }

在其他元素都出现两次的情况下，找到只出现一次的那一个数 leetcode No136. Single Number

int singleNumber(vector<int>& nums) {
        int a=0;
        for(int m:nums) {
            a^=m;
        }
        return a;
    }

在其他元素都出现两次的情况下，找到只出现一次的两个数 leetcode No260. Single Number III

假设只出现一次的两个数是a和b，先把所有数异或一遍，得到的结果是a^b。这时候要把a和b拆分开来，既然a和b是不相同的数，那么a异或b肯定至少有一位上是1，取出该位。取出这位有一个小技巧要记住（当遇到位运算的题，如果需要把数最右侧的1提取出来，可以通过 rightOne = eor & (~eor+1)得到。与上自己取反加一，或者 eor & (-eor)，如果我没理解错的话(~eor+1)=-eor 但是要判断是否为INT_MIN，防止溢出，因此完整表达为rightOne = ore==INT_MIN?ore:(ore & (-ore))）假设是00000100。然后，通过与操作判断出该位为1的元素，将所有该位为1的元素相异或，其中偶数项的元素相消了，剩下一个就是奇数项的其中一个数。

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        int ore=nums[0];
        for(int i=1;i<nums.size();++i) {
            ore^=nums[i];
        }
        //所有元素异或后，此时 ore 代表奇数个的两个数异或
        // 解法一  通过x&-x的方式得到x二进制中最右侧的1，但是要判断是否为INT_MIN，因为INT_MIN取相反数会超出INT_MAX，导致溢出，例如-128取相反数为128，超出127。
        int rightOne = ore==INT_MIN?ore:(ore & (-ore)); // 取出最右侧的1
        int a=0;
        for (int m : nums) {
            if ((m & rightOne) != 0 ) {
                a^=m;
            }
        }
        vector<int> result={a, a^ore};
        // 解法二 通过和1相与并不断右移，记录右移次数，直到找出为1的位
        /*int k=0;
        while((ore&1)==0){
            ore=ore>>1;
            ++k;
        }
        int ans1=0,ans2=0;
        for (int m: nums) {
            if((m>>k)&1!=0) ans1^=m;
            else ans2^=m;
        }
        vector<int> result={ans1, ans2};*/

        return result;

    }
};

哈希表

哈希表（hash table）也叫散列表
哈希表是根据关键码的值而直接进行访问的数据结构。
一般用于快速判断一个元素是否出现在集合里
时间复杂度O(1)
通过哈希函数将元素映射为哈希表上的索引，就可以通过查询索引下标快速判断元素是否出现了。
代码随想录哈希表理论基础

unordered_set常见操作：

查找元素find()，没有就返回最后一个元素的后一位元素

...
nums_set.find(num) != nums_set.end()
...

添加元素insert()

数组转unordered_set

unordered_set<int> nums_set(nums1.begin(), nums1.end());

unordered_set转数组

vector<int>(result_set.begin(), result_set.end());

eg:

// 求两个数组交集
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result_set; // 存放结果，之所以用set是为了给结果集去重
        unordered_set<int> nums_set(nums1.begin(), nums1.end());
        for (int num : nums2) {
            // 发现nums2的元素 在nums_set里又出现过
            if (nums_set.find(num) != nums_set.end()) {
                result_set.insert(num);
            }
        }
        return vector<int>(result_set.begin(), result_set.end());
    }
};

unordered_map常见操作：
find(key)：
查找以 key 为键的键值对，如果找到，则返回一个指向该键值对的正向迭代器；反之，则返回一个指向容器中最后一个键值对之后位置的迭代器（如果 end() 方法返回的迭代器）。
两数之和
umap[key]:返回value