动态规划：弗洛伊德（Floyd）算法总结与实现

弗洛伊德算法常用来来计算图中任意两点间的距离。

首先，我们把一个图初始化成一个各个顶点到其他顶点的距离的表格。弗洛伊德算法可以简单理解为更新这个初始化的表 成为 一个每个顶点到其他顶点都是最短距离的表格。

 其中，最关键的点就是：当这个图的一个顶点到其它顶点的距离有两个不同的过程，

1，经过一个中间节点距离最短

2，直接到达目的顶点距离最短

所以需要遍历每一个顶点 ，当这个顶点作为出发节点，中间节点，目的节点的情况时哪一个距离最短。

例如：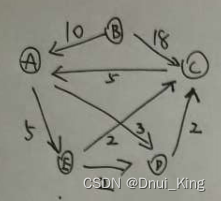

我们初始化这张表： （N表示不可以直接到达）

	j	A	B	C	D	E
i	0	0	0	0	0	0
A	0	0	N	N	3	5
B	0	10	0	18	N	N
C	0	5	N	0	N	N
D	0	N	N	0	0	N
E	0	N	N	2	2	0

 

举个例子来表示使用弗洛伊德算法来更新这张表的过程：

以A为出发节点

当从A->C时，原距离表中的距离是N，而存在D作为中间节点时，A->C的距离更新为A->D->C=3+2=5，5比N小，所以表更新为

	j	A	B	C	D	E
i	0	0	0	0	0	0
A	0	0	N	5	3	5
B	0	10	0	18	N	N
C	0	5	N	0	N	N
D	0	N	N	0	0	N
E	0	N	N	2	2	0

以此类推更新每一个节点。

算法的实现就是来比较这个表原有的距离与新找到的距离哪一个更短，如果找到了更短的，则更新表。

下面为代码实现，把不可到达定义成一个比较大的数：

package e.d7;

import java.util.Scanner;

/**
 * autor:张鑫
 */
//任意两点之间距离最短
public class Floyd {
    //定义不可到达
    static int UNLIMIT = 900;

    //取最小值
    static int minimum(int a, int b) {
        if (a <= b)
            return a;
        else
            return b;
    }

    //更新距离表和顶点前驱表
    static void floyd(int D[][]) {
        int k, i, j;
        int n = D.length - 1;
        for (k = 1; k <= n; k++) {
            for (i = 1; i <= n; i++) {
                for (j = 1; j < n; j++) {
                    D[i][j] = minimum(D[i][j], D[i][k] + D[k][j]);
                }
            }
        }
    }

    //更新表之后直接取最小值
    static int shortestRoute(int s, int t, int D[][]) {
        return D[s][t];
    }

    public static void main(String[] argv) {
//初始化表
        int D[][] = {
                {
                        0, 0, 0, 0, 0, 0
                },
                {
                        0, 0, UNLIMIT, UNLIMIT, 3, 5
                },
                {
                        0, 10, 0, 18, UNLIMIT, UNLIMIT
                },
                {
                        0, 5, UNLIMIT, 0, UNLIMIT, UNLIMIT
                },
                {
                        0, UNLIMIT, UNLIMIT, 2, 0, UNLIMIT
                },
                {
                        0, UNLIMIT, UNLIMIT, 2, 2, 0
                }
        };
        floyd(D);
        System.out.println("请输入任意两点所代表的数字,以求得任意两点间的最短距离");
        System.out.println("A-1B-2C-3D-4E-5");
        Scanner input = new Scanner(System.in);
        int i = input.nextInt();
        int j = input.nextInt();
        int shortest = shortestRoute(i, j, D);
        System.out.printf("从%d到%d的最短距离是%d\n", i, j, shortest);
    }
}