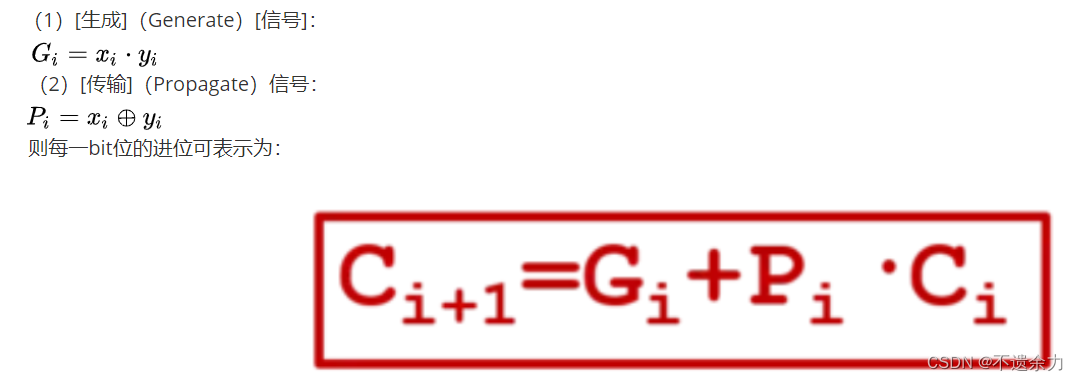加法器、半加器、全加器、超前进位加法器
一、半加器
简单来讲,半加器不考虑低位进位来的进位值,只有两个输入,两个输出。由一个与门和异或门构成.
真值表:
| 输入 | 输出 | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
半加器不考虑低位向本位的[进位],因此它不属于[时序逻辑电路],有两个输入端和两个输出。
设加数(输入端)为A、B ;和为S ;向高位的进位为Ci+1
逻辑表达式:
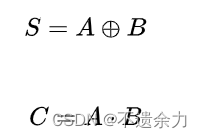
-
verilog 数据流级描述:
//半加器模块 module adder_half( input wire a, input wire b, output reg sum, output reg cout); always @(*) begin sum = a ^ b; cout = a & b; end endmodule-
RTL电路
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9eA7rSnS-1659874282111)(加法器、半加器、全加器、超前进位加法器.assets/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ZpdmlkMTE3,size_16,color_FFFFFF,t_70.png)]](https://images2.imgbox.com/21/94/oZ44fdQS_o.png)
-
二、全加器
全加器比半加器多了一位进位:
输入:A、B、Ci-1
输出:S、Ci
真值表:
| 输入 | 输出 | |||
|---|---|---|---|---|
| Ci-1 | Ai | Bi | Si | Ci |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
一位全加器的表达式如下:
Si=Ai⊕Bi⊕Ci-1
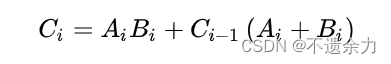
第二个表达式也可用一个异或门来代替或门对其中两个输入信号进行求和:
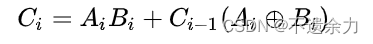
-
verilog代码实现一(用两个半加器和一个或门实现一个全加器)结构性描述:
//full_adder module adder_full(a,b,cin,,cout,sum); input a,b,cin; output cout,sum; wire w1,w2,w3; adder_half u1(.a(a),.b(b),.sum(w1),.cout(w2)); adder_half u2(.a(cin),.b(w1),.sum(sum),.cout(w3)); assign cout = w2 | w3; endmodule结构性描述的RTL电路
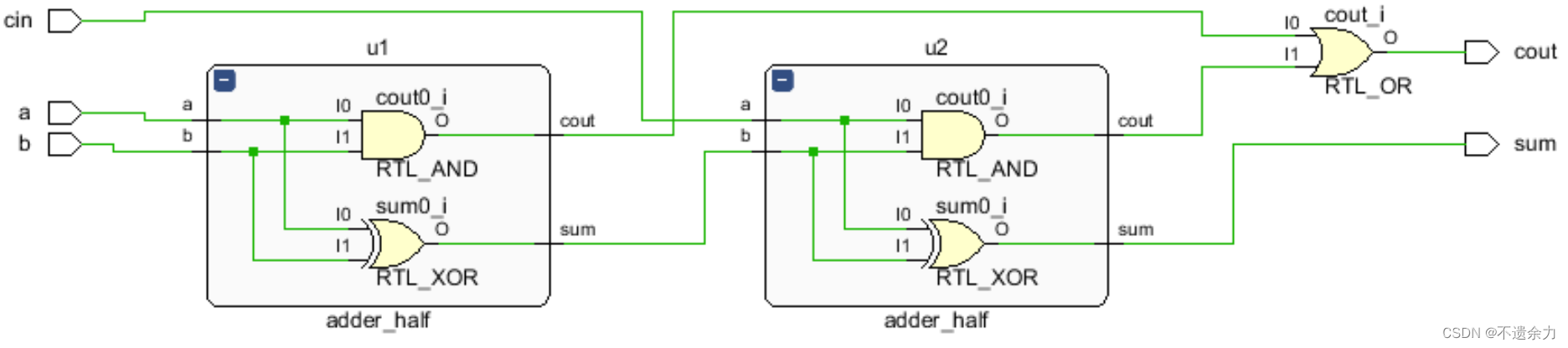
2.verilog代码实现二行为级描述:
//full_adder
module adder_full(a,b,cin,,cout,sum);
input a,b,cin;
output cout,sum;
assign {cout,sum} = a+b+cin;
endmodule
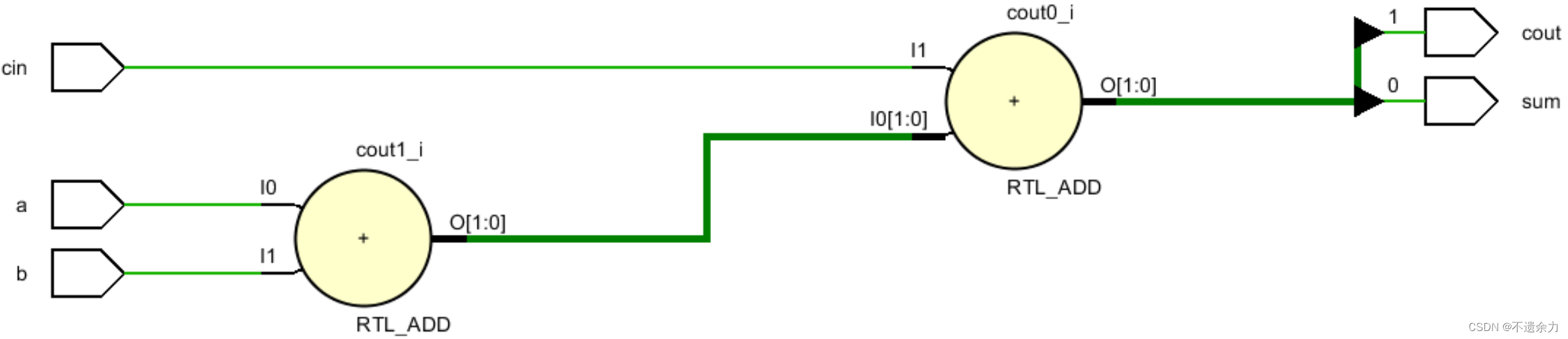
- 多位的全加器是依次进行相加的,延时高,频率低,被称为行波进位加法器。
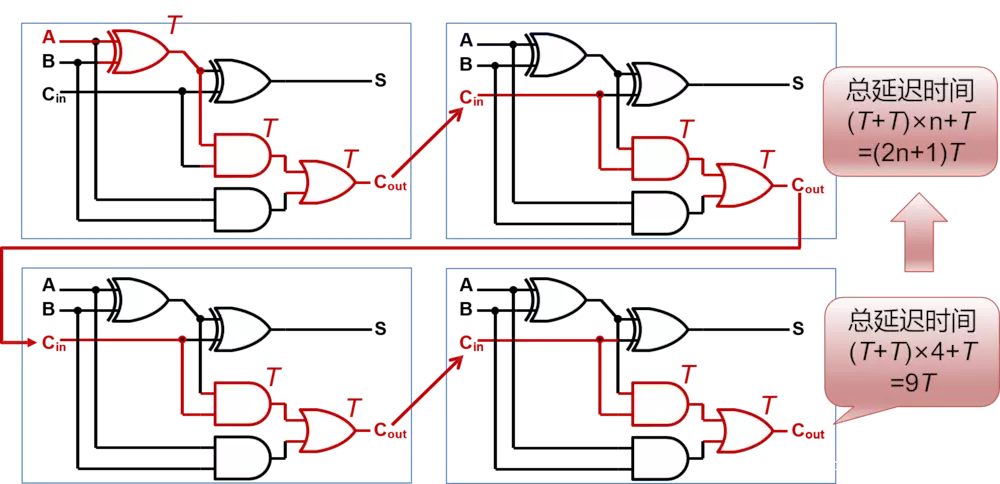
其关键路径如图中红线所示:则其延迟时间为(T+T)*4+T=9T。假设经过一个门电路的延迟时间为T。
对于一个n bit的行波加法器,其延时为(T+T)*n+T=(2n+1)T。
三、超前进位加法器
超前进位加法器(Carry-lookahead adder [1] )是对普通的全加器进行改良而设计成的并行加法器,主要是针对普通全加器串联时互相进位产生的延迟进行了改良。超前进位加法器是通过增加了一个不是十分复杂的逻辑电路来做到这点的
Si=Ai⊕Bi⊕Ci-1
考虑每一级的进位:
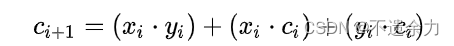
下面简述超前进位加法器的主要原理。我们先来考虑构成[多位加法器]的单个全加器从其低一位获得的进位[信号],我们可以将它变换为
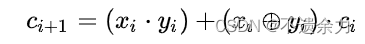
现在为二级制数的每一位[构建]两个新[信号]:
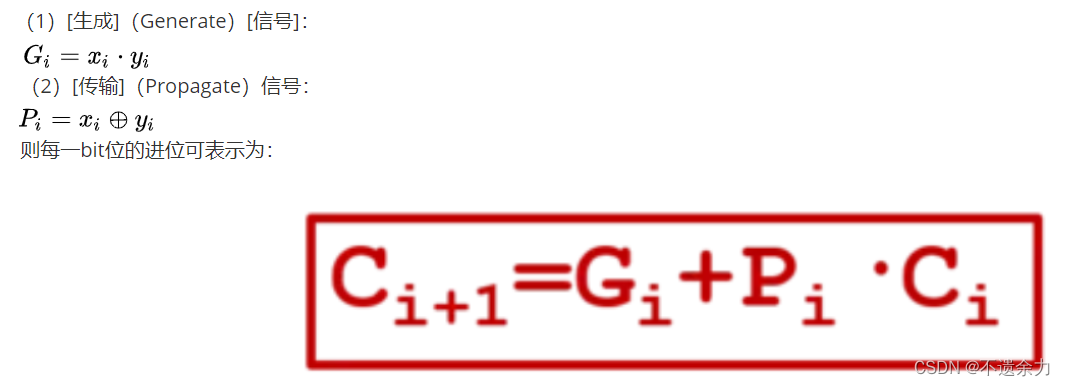
则对于4 bit的加法器,每个进位如下,可以看出,每个进位都不需要等待地位,直接计算可以得到。由此我们得到了提前计算进位输出的方法, 用这样的方法实现了加法器就被称为超前进位加法器
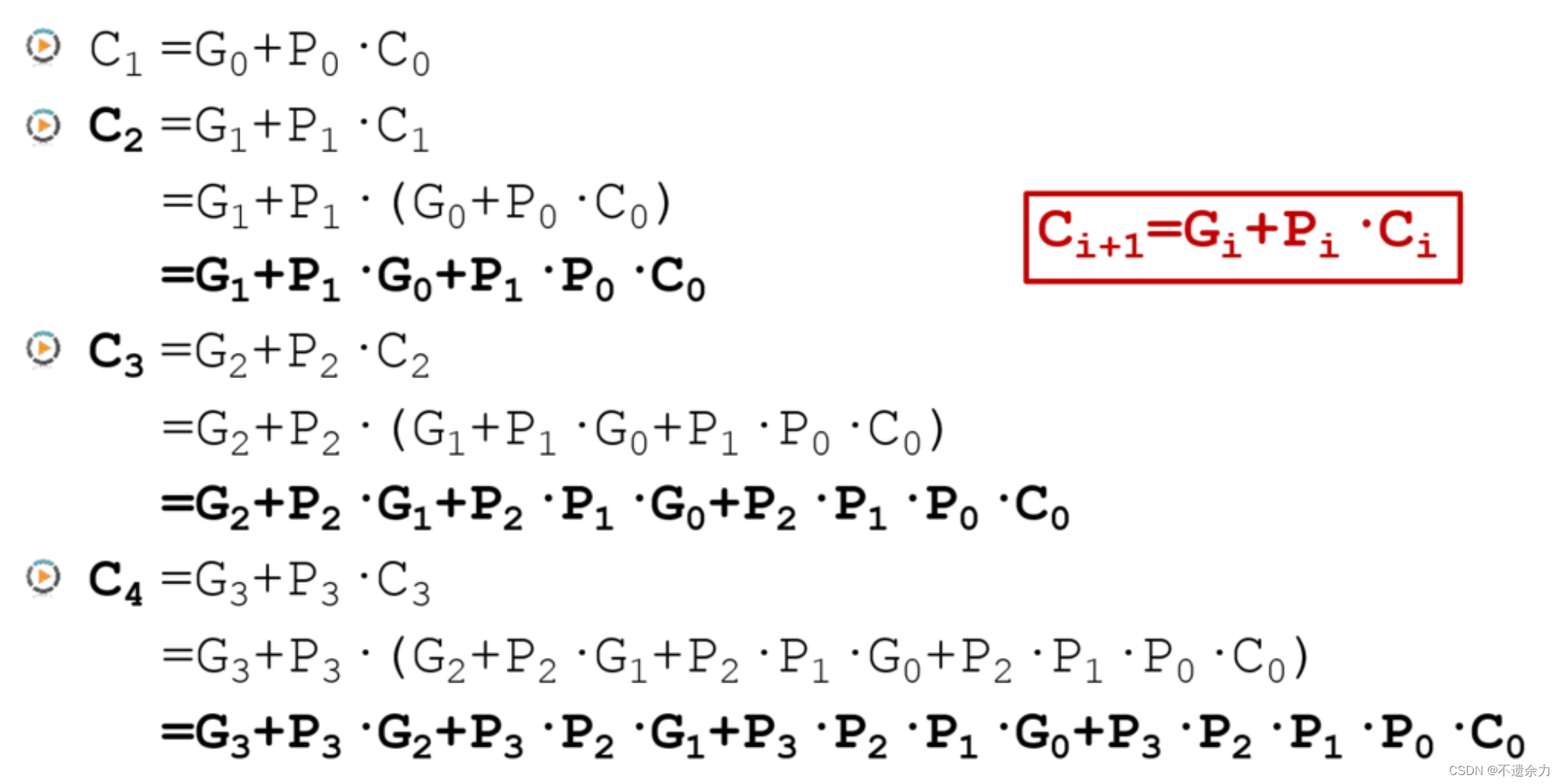
其组合电路如下:
进位延时只有三个门的延时,加上最后一级全加器的延时,最多四个延时时间。
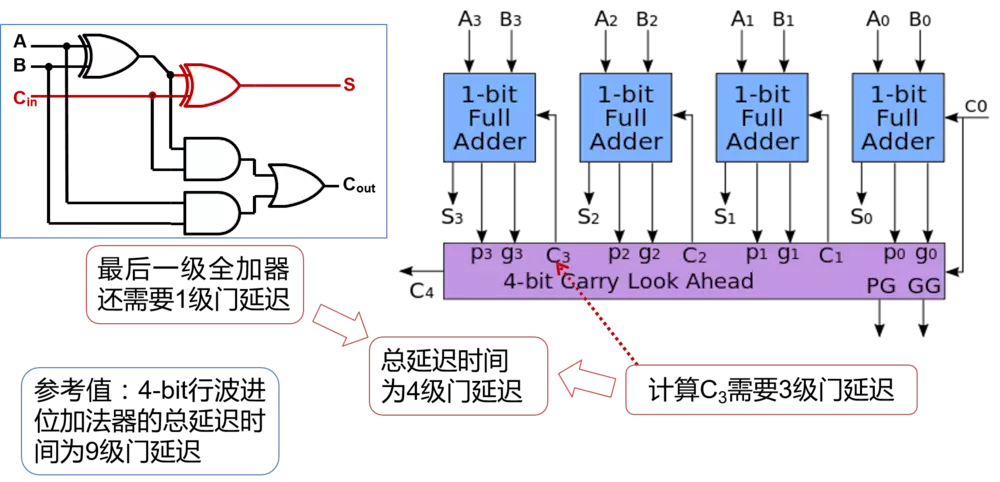
关键点
最关键的是:生成每个bit的进位信号、将进位信号进行依次合并
Si=Ai⊕Bi⊕Ci-1