Floyd算法思路以及扩展应用

Floyd模板

见这

Floyd算法思路

首先要假定不存在负环，因为有负环的话那么最短距离就无解了；

这个算法和SPFA一样是基于 D P DP DP的；

用 f ( k , i , j ) f(k,i,j) f(k,i,j)表示从 i i i出发，最终走到 j j j，经过的节点编号不超过 k k k的所有路径的最小值；

考虑最后一步，我们可以划分出包含节点 k k k与不包含节点 k k k两部分；

不包含节点 k k k那么就是 f ( k − 1 , i , j ) f(k-1,i,j) f(k−1,i,j)；

包含节点 k k k，那么路径分为 i → k i→k i→k加上 k → j k→j k→j两部分；

因为要求最小且两边互不影响，那么就是两边取最小；

则为 f ( k − 1 , i , k ) + f ( k − 1 , k , j ) f(k-1,i,k)+f(k-1,k,j) f(k−1,i,k)+f(k−1,k,j)

因此得到状态转移方程

f ( k , i , j ) = m i n { f ( k − 1 , i , j ) , f ( k − 1 , i , k ) + f ( k − 1 , k , j ) } f(k,i,j)=min\{f(k-1,i,j),f(k-1,i,k)+f(k-1,k,j)\} f(k,i,j)=min{f(k−1,i,j),f(k−1,i,k)+f(k−1,k,j)}；

然后我们发现，第 k k k层只会用到第 k − 1 k-1 k−1层；

因此我们可以使用最常见的滚动数组优化；

则有 f ( i , j ) = m i n { f ( i , j ) , f ( i , k ) + f ( k , j ) } f(i,j) = min\{f(i,j),f(i,k)+f(k,j)\} f(i,j)=min{f(i,j),f(i,k)+f(k,j)}

Floyd应用场景

  • 任意两点最短路
  • 传递闭包
  • 找最小环
  • 恰好经过 k k k条边的最短路（倍增)

牛的旅行

传送门

这题是Floyd求最短路的简单扩展；

题面

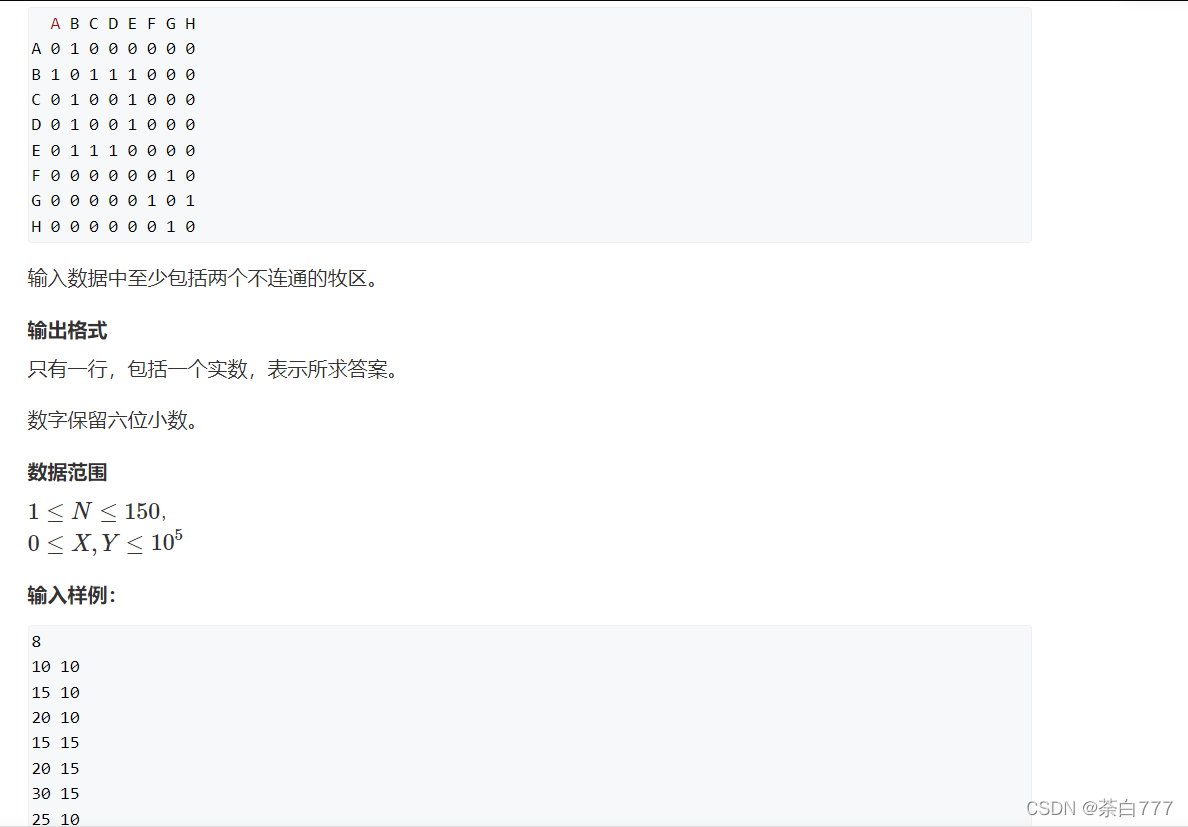
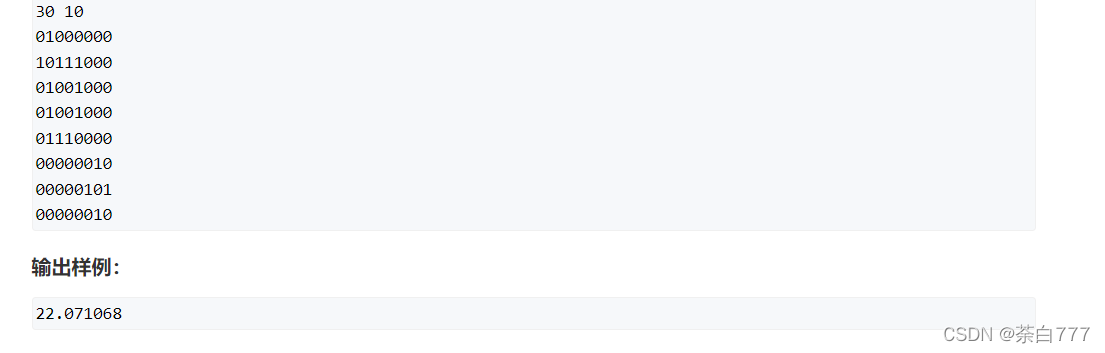
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

思路

题目要求我们连一条边以后，使得新牧场的直径最小；

假设左边牧场的直径为 d 1 d_1 d1​，右边牧场的直径为 d 2 d_2 d2​；

因为我们要将这两个牧场连起来，那么假设新的直径为 d 3 d_3 d3​；

必然有 d 3 ≥ m a x ( d 1 , d 2 ) d_3 ≥ max(d1,d2) d3​≥max(d1,d2)；

因为要求最小，我们期望相等；

假设连边以后，构成了一条新的直径；

那么组成必然是距离左边点的最远距离+这条路径长+距离右边点的最远距离；

我们想要相等，要么取原来的直径，要么这个直径与之前最大的直径相等；

也就是说，这条路径我们想要最小；

流程如下；

  • 跑Floyd
  • 求每个点的最远距离，记为 m a x d i maxd_i maxdi​
  • 求最小的新路径 d 3 d_3 d3​
  • 取 m a x ( d 1 , d 2 , d 3 ) max({d_1,d_2,d_3}) max(d1​,d2​,d3​)

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <utility>
#include <cmath>

using namespace std;

typedef long long ll;

const int N = 200 + 10;

typedef pair<int,int> pii;
const double INF = 1e20;
int n;
char G[N][N];
double dist[N][N];
double get_dis(pii p,pii q){
    int dx = p.first - q.first;
    int dy = p.second - q.second;
    return sqrt(dx*dx + dy*dy);
}
double max_dist[N];
void floyd(){
    for(int k=0;k<n;++k)
        for(int i=0;i<n;++i)
            for(int j=0;j<n;++j)
                dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);
    
}
void solve(){
    cin >> n;
    vector<pii> ve;
    for(int i=1;i<=n;++i){
        int x,y;
        cin >> x >> y;
        ve.push_back({x,y});
    }
    for(int i=0;i<n;++i)
        cin >> G[i];
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            if(i != j){
                if(G[i][j] == '1')
                    dist[i][j] = get_dis(ve[i],ve[j]);
                else
                    dist[i][j] = INF;
            }
    floyd();

    double ans1 = 0;
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            if(dist[i][j] < INF/2)
                max_dist[i] = max(max_dist[i],dist[i][j]);
    
    for(int i=0;i<n;++i) ans1 = max(ans1,max_dist[i]);
    
    double ans2 = INF;
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            //没有边才能连边
            if(dist[i][j] >= INF/2)
                ans2 = min(ans2,max_dist[i]+max_dist[j]+get_dis(ve[i],ve[j]));
    printf("%.6f\n",max(ans1,ans2));
}

signed main(){
    //std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int t = 1;
    //cin >> t;
    while(t--)
        solve();
    return 0;
}

排序

传送门

本题应用了Floyd求传递闭包；

传递闭包概念

将所有间接相连的点，我们给它连一条直接相连的边，这样就是一个传递闭包了；

比如下图，橙色是我们连上的，蓝色是原图；

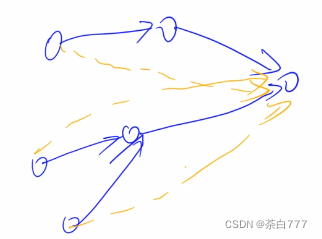
在这里插入图片描述

Floyd求传递闭包的步骤

设 g ( i , j ) = 1 g(i,j)= 1 g(i,j)=1表示 i i i与 j j j之间有一条直接相连的边；
设 g ( i , j ) = 0 g(i,j)=0 g(i,j)=0表示 i i i与 j j j之间没有相连的边；

我们用 d ( i , j ) d(i,j) d(i,j)表示求完传递闭包以后， i i i与 j j j之间是否相连；

初始化， d ( i , j ) = g ( i , j ) d(i,j)=g(i,j) d(i,j)=g(i,j);

接着三重循环，最后一步更新改一下即可

for k
	for i
		for j
			if(d(i,k) && d(k,j)) d(i,j) = 1

接着用这道题讲一下应用方法；

题面

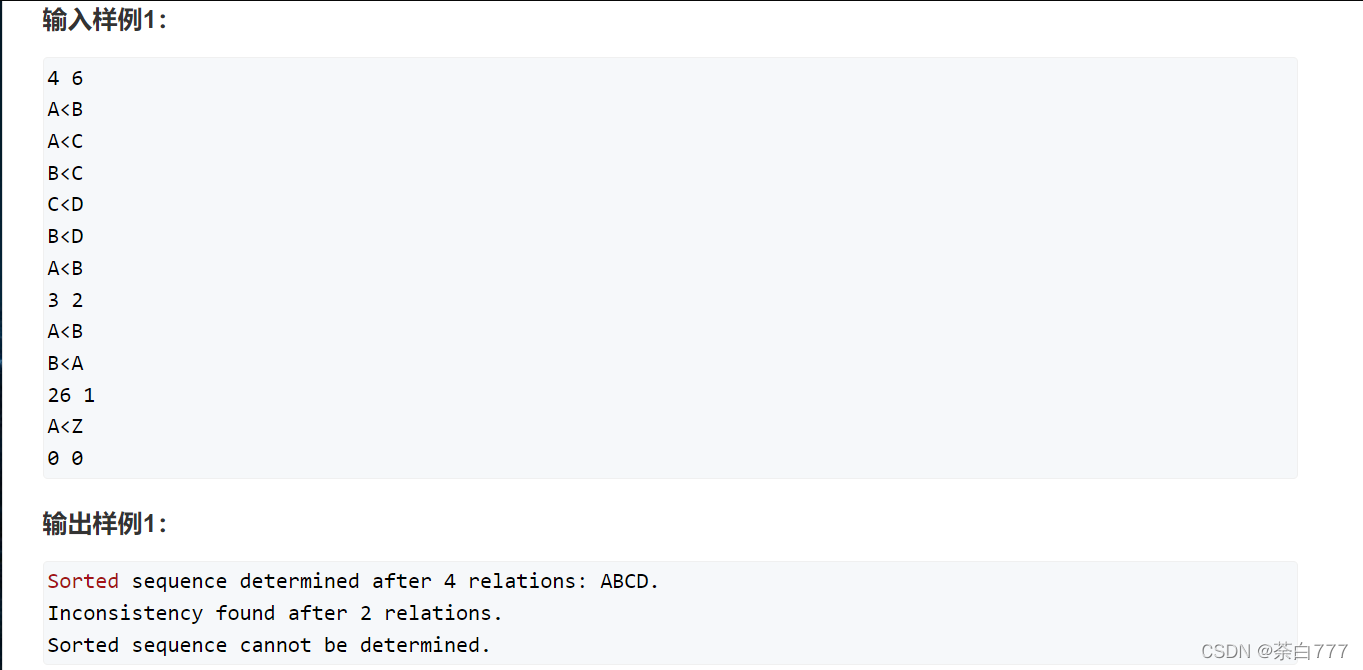
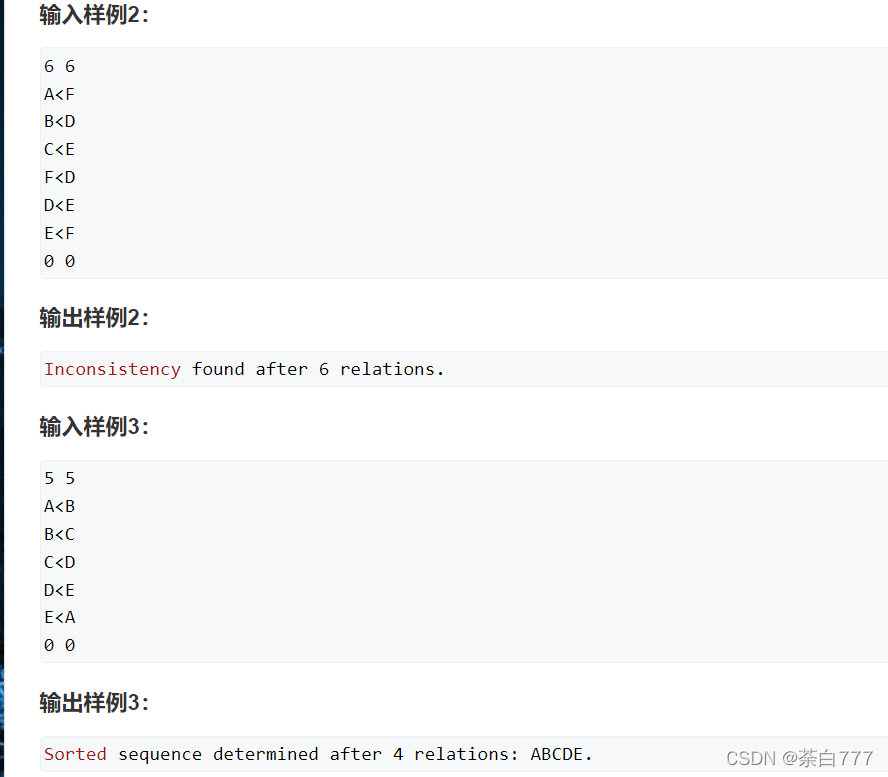
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

思路

我们用 g ( i , j ) g(i,j) g(i,j)来表示 i i i与 j j j之间的关系；

设 i < j i<j i<j，则 g ( i , j ) = 1 g(i,j) = 1 g(i,j)=1

若不能确定关系则 g ( i , j ) = 0 g(i,j)=0 g(i,j)=0

每输入一条关系，我们就跑一次Floyd求传递闭包；

步骤跟上面提到的一样，先初始化 d ( i , j ) = g ( i , j ) d(i,j) = g(i,j) d(i,j)=g(i,j)；

当 A < B , B < A → A < A A<B,B<A→A<A A<B,B<A→A<A，即 d ( i , i ) = 1 d(i,i) = 1 d(i,i)=1的时候，我们认为有矛盾；

当任意的 d ( i , j ) = 0 且 d ( j , i ) = 0 d(i,j) = 0 且 d(j,i) = 0 d(i,j)=0且d(j,i)=0时，则目前不能确定关系；

如果以上都没发生，则确认关系；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <string>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 30 + 10;

int n,m;
//这里的d只是方便理解，将所有的d换成g照样ok；
bool g[N][N],d[N][N];

void floyd(){
    //初始化d(i,j) = g(i,j)
    memcpy(d,g,sizeof d);
    for(int k=1;k<=n;++k)
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j)
                d[i][j] |= d[i][k] && d[k][j];
}

int check(){
    for(int i=1;i<=n;++i)
        //矛盾
        if(d[i][i]) return 2;
    for(int i=1;i<n;++i)
        for(int j=i+1;j<=n;++j)
            //存在一对(i,j) 不能确定
            if(!d[i][j] && !d[j][i]) return 0;
    //有解
    return 1;
}
bool vis[N];//判断某个点是否被输出了
void output_min(){
    for(int i=1;i<=n;++i){
        if(!vis[i]){
            bool f = 1;
            //看其他点是否比我们小
            //如果不存在一个点比我们小，则我们是最小的
            for(int j=1;j<=n;++j){
                if(i == j) continue;
                if(!vis[j] && d[j][i]){
                    //存在比我们小的
                    f = 0;
                    break;
                }
            }
            if(f){
                vis[i] = 1;
                putchar('A' + i - 1);
            }
        }
    }
}
void solve(){
    memset(g,0,sizeof g);
    memset(d,0,sizeof d);
    string str;
    int type = 0;//0为不确定，1为唯一确定，2为矛盾
    int cnt = 0;
    for(int i=1;i<=m;++i){
        cin >> str;
        int a = str[0] - 'A' + 1,b = str[2] - 'A' + 1;
        if(!type){
            g[a][b] = 1;// a < b
            floyd();
            type = check();
            cnt = i;
        }
    }
    if(type == 0){
        cout << "Sorted sequence cannot be determined.\n";
    }
    else if(type == 1){
        memset(vis,0,sizeof vis);
        printf("Sorted sequence determined after %d relations: ",cnt);
        //每次输出最小值
        for(int i=1;i<=n;++i) output_min();
        printf(".\n");
    }
    else{
        printf("Inconsistency found after %d relations.\n",cnt);
    }
}

signed main(){
    while(cin >> n >> m,n || m)
        solve();
    return 0;
}

观光之旅

传送门

题面

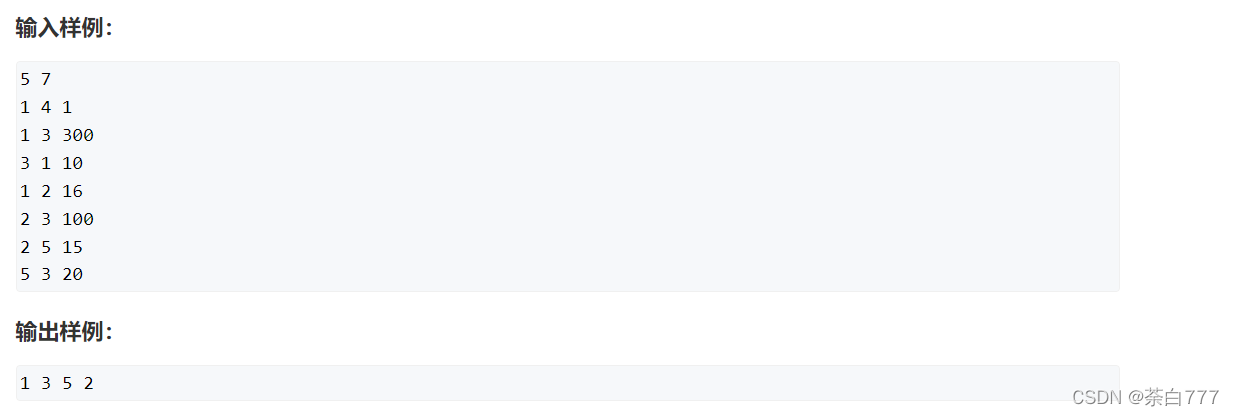
在这里插入图片描述
在这里插入图片描述

思路

做这题之前首先介绍几个Floyd的性质；

for(k=1~n)
	for (i=1~n)
		for (j=1~n)

当执行到第 k k k步的时候；

对于 d ( i , j ) d(i,j) d(i,j)来说，我们知道了只经过 1 1 1 ~ k − 1 k-1 k−1的最短路径；

且当前加进来最大的节点是 k k k；

又因为题目要求环上有 3 3 3个点即可，我们的 k k k是 1 1 1 ~ n n n都会取到；

那么我们只需要枚举所有以 k k k为最大节点的环即可不遗漏的枚举完所有的解，从中取一个min就行；

最小环肯定是这个形状的；

在这里插入图片描述
我们枚举到第 k k k个节点的时候，左边恰好就是 d ( i , j ) d(i,j) d(i,j)，即只经过 1 1 1 ~ k − 1 k-1 k−1的最短路径；

即最小值为 m i n { d ( i , j ) + w ( i , k ) + w ( k , j ) } min\{d(i,j)+w(i,k)+w(k,j)\} min{d(i,j)+w(i,k)+w(k,j)}

有了上个式子，我们已经求出了最小环；

现在考虑如何记录方案；

在 d p dp dp问题求具体方案中，我们知道是不能压缩维数的，比如背包求具体方案就不能压缩成一维的，需要二维；

但在Floyd最短路中，不压维数是三维的，但这有一个性质，可以使得我们不压缩维数，使用二维；

首先，我们不需要考虑重复的点，因为假设环上有重复的点；

在这里插入图片描述

因为题干中边权至少为 1 1 1，那么我们把它去掉显然是更优秀的答案；

在这里插入图片描述

即最小环上必然不存在重复点；

假设 ( i , j ) (i,j) (i,j)的中间点是 k k k；

( i , k ) (i,k) (i,k)的中间点是 k 1 k_1 k1​， ( k , j ) (k,j) (k,j)的中间点是 k 2 k_2 k2​

因为上面提到了不会有重复点，那么 k 1 ≠ k 2 k_1≠k_2 k1​​=k2​；

并且递归下去也是成立的；

那么也就是说，用二维来表示我们的状态并不会重叠、覆盖，也就不需要多加一维了；

我们可以用 p o s ( i , j ) pos(i,j) pos(i,j)表示 ( i , j ) (i,j) (i,j)的中间点是谁；

维护起来也很简单，就在更新最短路的时候即可；

if(d(i,j) > d(i,k) + d(k,j)){
	d(i,j) = d(i,k) + d(k,j);
	pos(i,j) = k;
}

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e2 + 10;

int dist[N][N],w[N][N],pos[N][N];

const int INF = 0x3f3f3f3f;

int cnt,path[N];
void insert_path(int i,int j){
    int k = pos[i][j];
    if(k == 0) return;
    insert_path(i,k);
    path[++cnt] = k;
    insert_path(k,j);
}
void solve(){
    int n,m;
    cin >> n >> m;
    memset(w,0x3f,sizeof w);
    for(int i=1;i<=n;++i) w[i][i] = 0;
    while(m--){
        int u,v,val;
        cin >> u >> v >> val;
        w[u][v] = w[v][u] = val;
    }
    memcpy(dist,w,sizeof dist);
    ll mn = INF;//最小环的长度
    for(int k=1;k<=n;++k){
        //目前最大的点是k，还未插入
        //只需要枚举1~k-1的点对(i,j)
        for(int i=1;i<k-1;++i){
            for(int j=i+1;j<k;++j){
                //dist、w可以达到1e9级别，防止溢出
                if(1ll*dist[i][j] + w[i][k] + w[k][j] < mn){
                    mn = 1ll*dist[i][j] + w[i][k] + w[k][j];
                    cnt = 0;
                    //i -> k -> j -> i
                    path[++cnt] = i;
                    path[++cnt] = k;
                    path[++cnt] = j;
                    insert_path(j,i);
                }
            }
        }
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                if(dist[i][j] > dist[i][k] + dist[k][j]){
                    dist[i][j] = dist[i][k] + dist[k][j];
	                pos[i][j] = k;
                }
            }
        }
    }
    if(mn == INF){
        cout << "No solution.\n";
        return;
    }
    for(int i=1;i<=cnt;++i) cout << path[i] << ' ';
    cout << '\n';
}

signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int t = 1;
    while(t--)
        solve();
    return 0;
}

牛站

传送门

这题是求恰好经过 k k k条边的最短路（倍增)；

是Floyd的变形；

题面

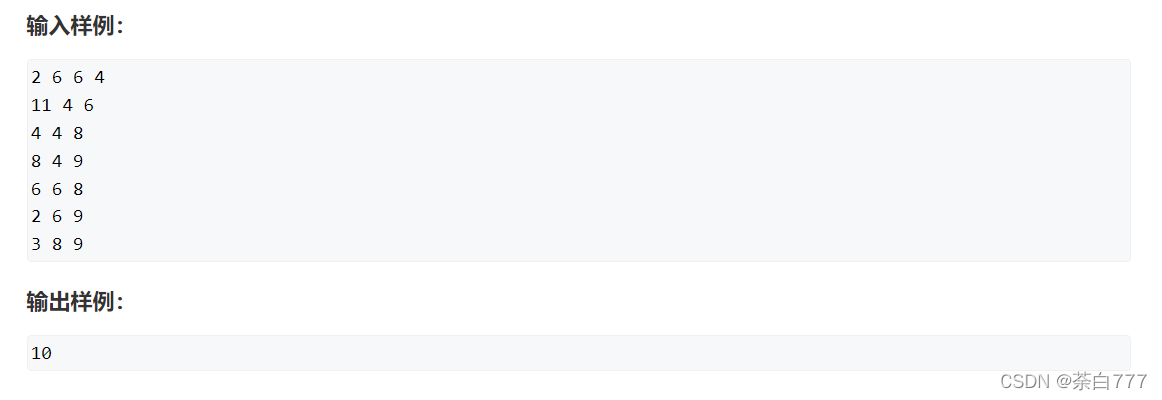
在这里插入图片描述
在这里插入图片描述

思路

传统的Floyd的 f ( k , i , j ) f(k,i,j) f(k,i,j)的状态表示为从 i i i到 j j j只经过 1 1 1~ k k k的话，最短路径是多少；

这题的状态 f ( k , i , j ) f(k,i,j) f(k,i,j)表示为从 i i i到 j j j，恰好经过 k k k条边的最短路径；

假设 k k k是 i , j i,j i,j的中间点，如下；

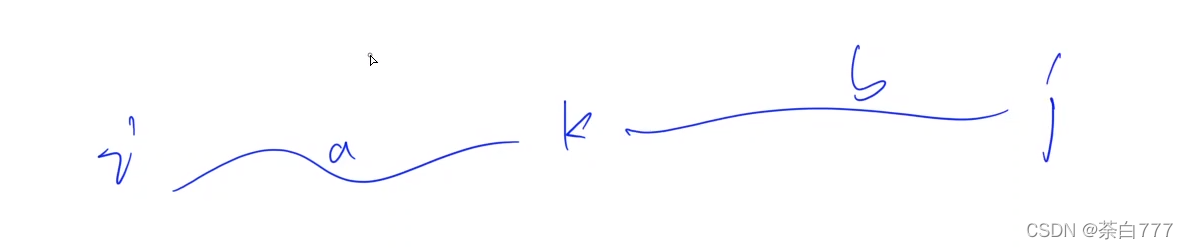
在这里插入图片描述
要取最小值，因为两段路不会互相影响，那么 i → k i→k i→k， k → j k→j k→j分别最小即可；

即状态转移为 f ( a + b , i , j ) = m i n { f ( a , i , k ) + f ( b , k , j ) } f(a+b,i,j)=min\{f(a,i,k)+f(b,k,j)\} f(a+b,i,j)=min{f(a,i,k)+f(b,k,j)}；

这里是三个点的情况，现在我们扩展到 n n n个点；

在这里插入图片描述

因为每一段都是独立的，那么也就是说先求哪一部分都是没有区别的；

换句话说，我们将每段路径分别表示为 d 1 , d 2 , . . . , d n d_1,d_2,...,d_n d1​,d2​,...,dn​

那么答案就是 d 1 + d 2 + . . . + d n d_1+d_2+...+d_n d1​+d2​+...+dn​；

由于先求哪一部分都是没影响的(因为路径之间两两独立)，也就是说这个求和满足结合律；

满足结合律有一个好处，我们可以类比矩阵乘法，矩阵乘法也是满足结合律但是不满足交换律的；

矩阵乘法我们知道有一个操作叫矩阵加速，或者说类似快速幂的思想，我们可以用倍增来优化这个求解的过程；

原本是每求一段就加一，时间复杂度是 O ( n ) O(n) O(n)级别的；

我们现在用倍增来求，先求一，再求二，然后求四，八…，这样时间复杂度就是 O ( l o g n ) O(logn) O(logn)级别的；

也就是按 f ( 1 , i , j ) → f ( 2 , i , j ) → f ( 4 , i , j ) → f ( 8 , i , j ) → . . . f(1,i,j)→f(2,i,j)→f(4,i,j)→f(8,i,j)→... f(1,i,j)→f(2,i,j)→f(4,i,j)→f(8,i,j)→...，这个顺序；

上面介绍完了主要思路，这里提一点注意事项；

因为点的取值是 1 → 1000 1→1000 1→1000，而边数只有 100 100 100个，每条边至多新增两个点，也就是最多 200 200 200个点，因此我们需要离散化一下；

这样总的时间复杂度就是 O ( T 3 l o g N ) O(T^3logN) O(T3logN)

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <unordered_map>
#include <cmath>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 210 + 10;

int k,m,S,E;
int dist[N][N]; //dist(i,j)其实是f(1,i,j)

unordered_map<int,int> id_mp;
int n;
int get(int x){
    //这里不需要顺序 无序离散化即可
    if(!id_mp.count(x)) id_mp[x] = ++n;
    return id_mp[x];
}
int tmp[N][N];
void extend_floyd(int ret[][N],int a[][N],int b[][N]){
    memset(tmp,0x3f,sizeof tmp);
    for(int k=1;k<=n;++k)
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j)
                tmp[i][j] = min(tmp[i][j],a[i][k] + b[k][j]);
    memcpy(ret,tmp,sizeof tmp);//ret = tmp
}
void qpow(){
    int ret[N][N];//零元，相当于f(0,i,j)
    int base[N][N];
    memcpy(base,dist,sizeof base);
    memset(ret,0x3f,sizeof ret);
    for(int i=1;i<N;++i) ret[i][i] = 0;
    while(k){
        if(k&1) extend_floyd(ret,ret,base);//ret *= base;
        extend_floyd(base,base,base);//base *= base;
        k>>=1;
    }
    cout << ret[S][E] << '\n';
}
void solve(){
    memset(dist,0x3f,sizeof dist);
    //注意这里不能这样初始化，这样初始化相当于i -> i 恰好经过一条长度为0的边
    //注意dist数组的定义
    //for(int i=1;i<N;++i) dist[i][i] = 0;
    cin >> k >> m >> S >> E;
    S = get(S),E = get(E);
    while(m--){
        int u,v,w;
        cin >> w >> u >> v;
        u = get(u),v = get(v);
        dist[u][v] = dist[v][u] = min(dist[u][v],w);
    }
    qpow();
}

signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int t = 1;
    //cin >> t;
    while(t--)
        solve();
    return 0;
}

对比

在这里插入图片描述
在这里插入图片描述

总结

通过这道题目，我们就得到了一个求解Floyd的新思路；

虽然这种思路时间复杂度比经典版本的高，但是因为是准确的 k k k条边，因此即使有负环也不会一直兜圈子，也是可以求解的；