信号完整性(SI)电源完整性(PI)学习笔记(二十二)差分对与差分阻抗(二)
差分对与差分阻抗(二)
1.实际耦合影响
当我们把两条带状线靠得很近时,它们的边缘电场和磁场就会互相覆盖之间的耦合强度也会很强。由电容和电感矩阵元素描述的耦合与所加电压完全无关,它只与导线的几何结构和材料特性有关。两条信号线的间距越小,他们之间的耦合就越强。
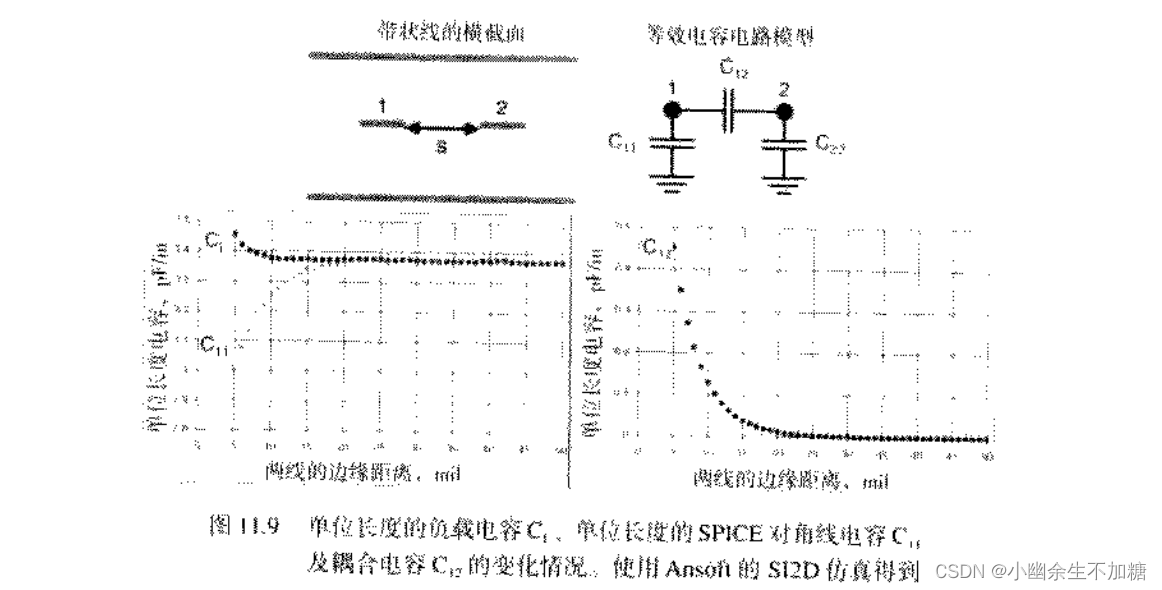
2.当两条信号线距离非常近时,邻近信号线的存在将会影响线1的阻抗称为接近效应。
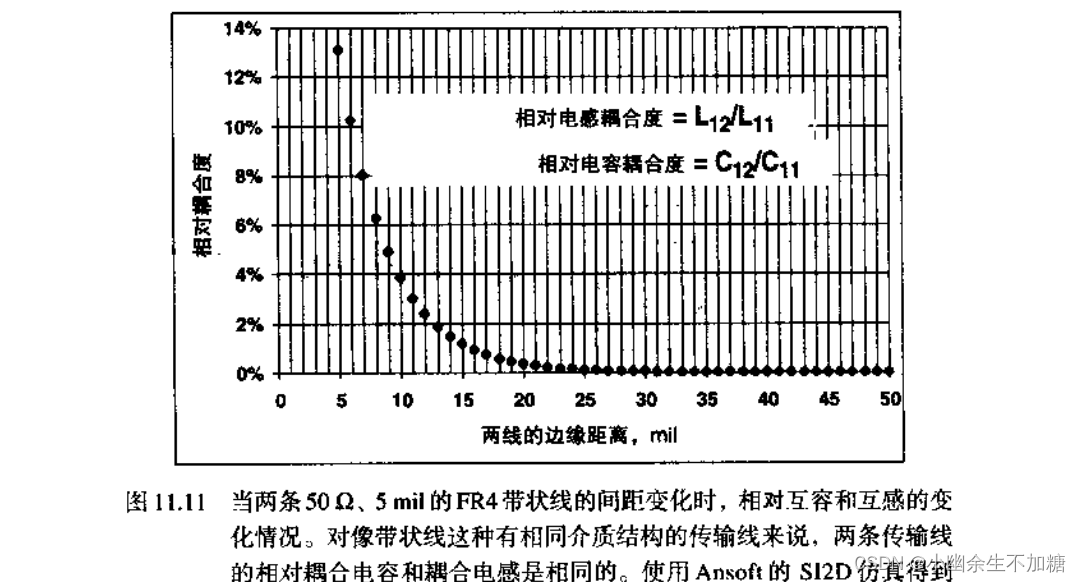
(1)两条信号线由方向相反的两个信号跳变驱动,电流从驱动器流进信号线1,然后流向返回路径,当两条信号线靠近时,为了驱动单端信号线更大的电容,这个电流将会增大。如果所加电压没有变化而电流增加,则对驱动器而言,意味着输入阻抗减小。当给第二条信号线加上相反的信号,第一条信号线的单端特性阻抗会减小;
(2)假设给第二条信号线加上与第一条信号相同的信号,只有电容C11存在,这就意味着要驱动的电容减小了。此时流经信号线1的电流为:

3.我们发现,当有第二条临近信号线存在时,信号线1的特性阻抗不是一个特定的值,它还取决于邻近信号线被驱动的情况。
(1)如果信号线2被固定在0电位,则阻抗值接近于未耦合时的值;
(2)如果信号线2加相反信号,阻抗值就会降低;
(3)如果信号线2加相同信号,阻抗值就会升高。
差分信号在这两条信号上分别驱动两个相反的信号。正如前面所讨论的,此时每条信号线的阻抗会因为彼此之间的耦合而减小。
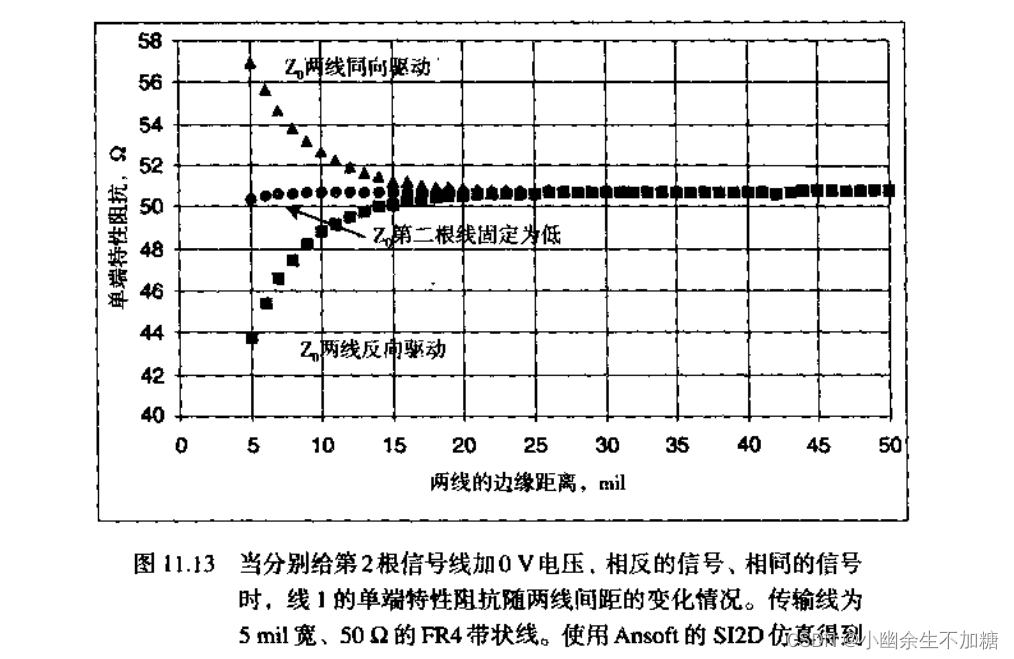
4.只处理单端信号,一条传输线仅用一个阻抗描述。但是当他是一对线中的一个且存在耦合时,需要用3种不同阻抗加以描述。
当两条信号线的间距逐渐减小时,差分阻抗的变化情况,对带状线而言,相比于线间距等于3倍线宽的无耦合情况,在可制造的最小间距(如线间距等于线宽)下,存在耦合时的差分阻抗也仅仅减小了12%。
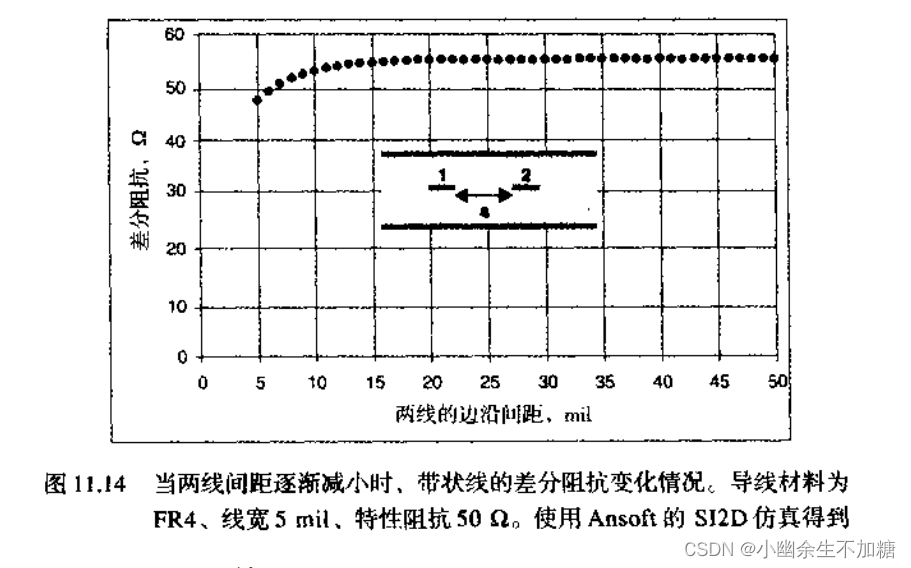
5.五种分析计算差分阻值的变化
(1)直接使用近似式的结果;
(2)直接使用场求解器的结果;
(3)采用基于模态的分析;
(4)采用基于电容和电感矩阵的分析;
(5)采用基于阻抗矩阵的分析。
近似式:微带线差分阻抗的近似式:

耦合带状线,差分阻抗近似为:
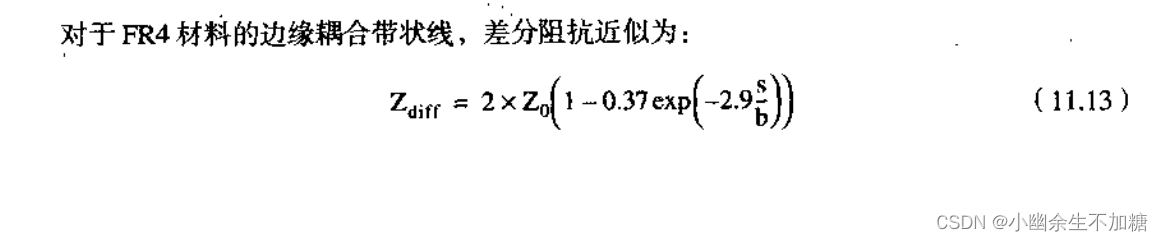
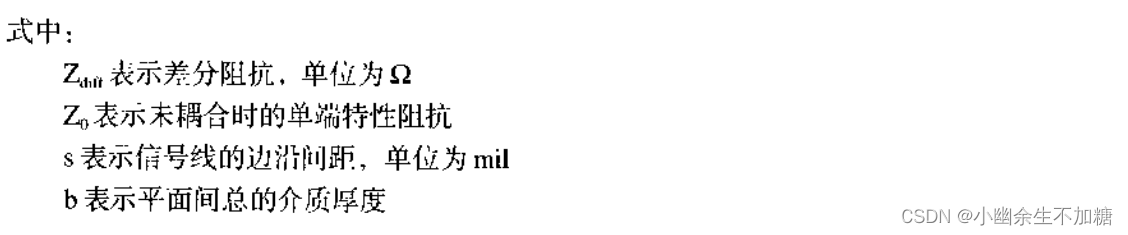
准确场求解器计算:这里,近似算法先要借用场求解器给出的单端特性阻抗,再用近似就能预估出耦合对差分阻抗产生的轻微影响。只要给出特性阻抗初始值是正确的,这种近似误差在1%~10%之间。
运用场求解器的一个优势在于:在很多种几何结构中,基于此方法的一些计算工具的误差在1%以下。当准确度要求比较严格时,比较交付制造使用PCB版图的签发,这时唯一能够用的工具就是核验过的二维场求解器。绝对不能将近似式运用到设计签发当中。
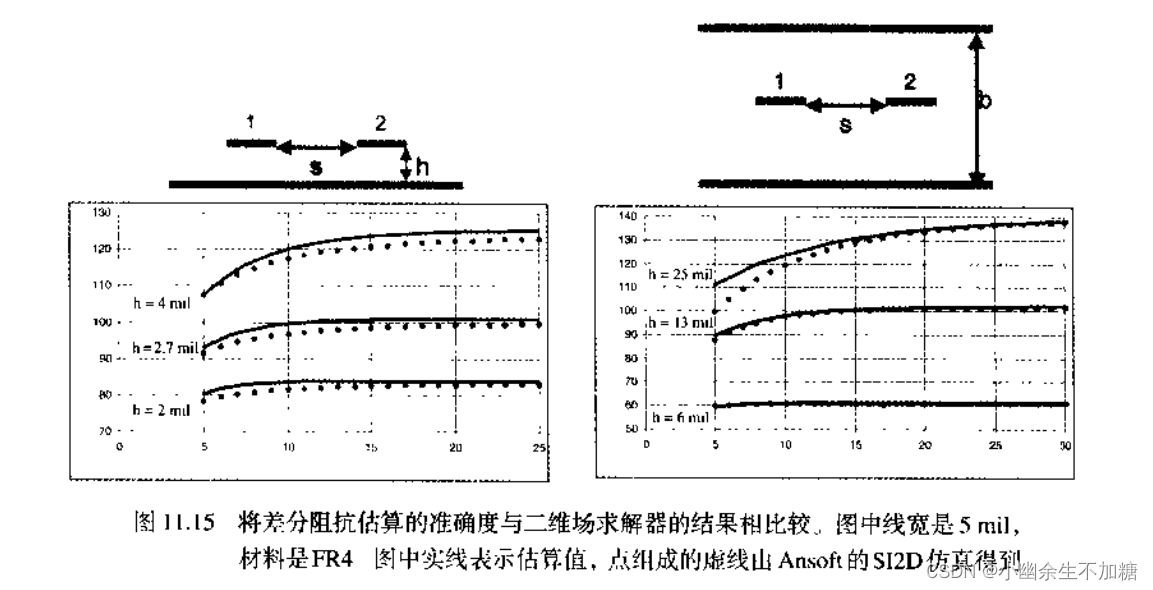
6.一条信号线上的差分信号的返回电流由另一条信号线运送,等量电流从一条信号线流入,再从另一条信号线流出,这的确是事实,但并不是事实的全部。
因为这里差分对的两条信号线的线间距比较大,所以当用差分信号驱动时,返回平面中的电流不出现重叠。此时返回路径平面的总电流为0,但每条信号线下的平面中都有确定的局部电流分布,任何改变电流分布的因素都将会改变差分对的差分阻抗。

7.当差分对的信号线与返回路径平面之间的耦合程度大于两条信号之间的耦合时,返回路径平面中就会出现两路不同的相互分离的电流,并且返回路径电流分布只出现微小的重叠,返回路径电流分布严重制约差分对的差分阻抗,返回路径电流分布的扰动直接影响到差分阻抗。
8.对于任何一对公用返回导体的单端传输线而言,如果返回导体距信号走线足够远,差分信号的返回导体电流分布就相互重叠,并完全抵消掉。此时返回路径导体的存在对差分阻抗产生不了任何影响。这种特定的条件下,第一条信号线上的返回电流将完全可能由另一条信号线运送,有以下3种需要关注。
(1)边缘耦合微带线,返回平面足够远;
(2)双绞线电缆;
(3)宽边耦合带状线,返回平面足够远。
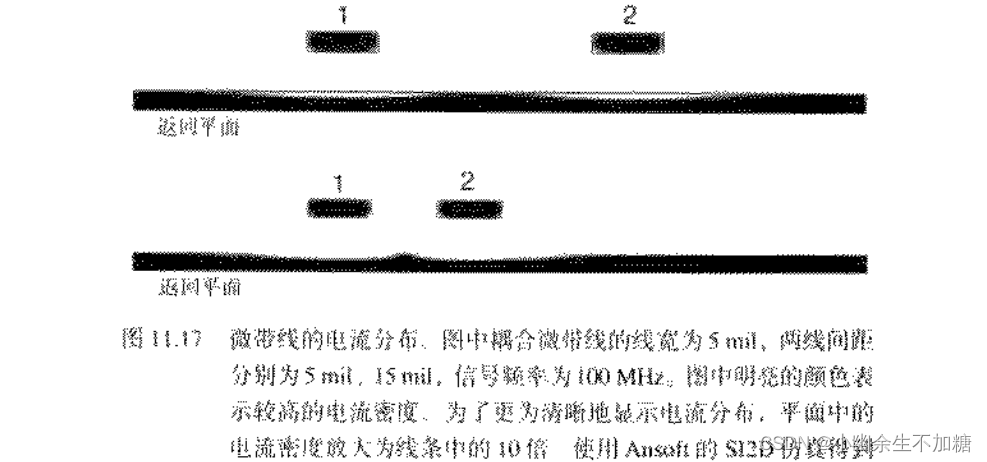
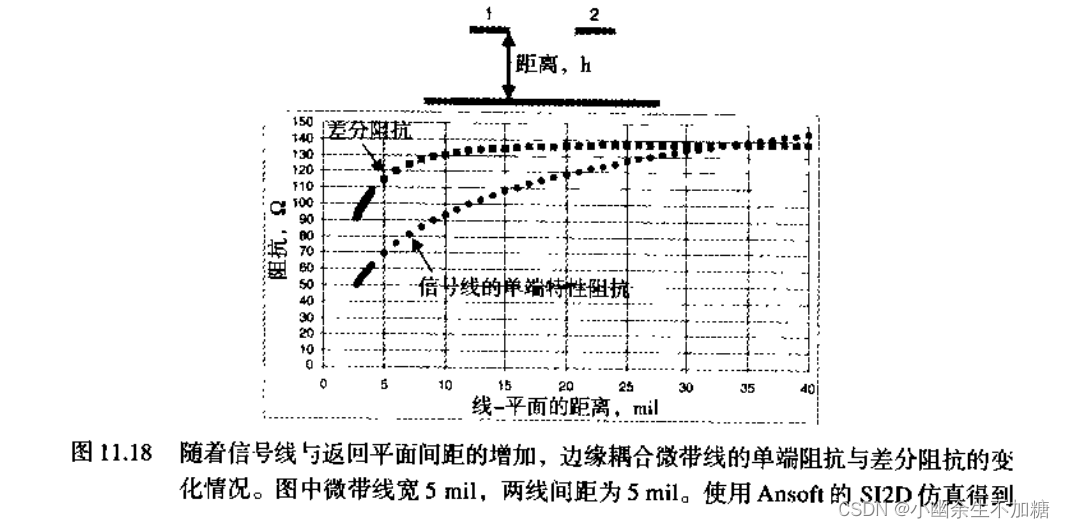
9.当信号线阻抗约为50Ω,线间距最小时,返回平面中有明显的电流分布,平面的存在将影响差分阻抗。如果将平面移到更远处,那么每条线的单端阻抗将会增加,差分阻抗也将会增加。然而,随着平面越移越远,差分信号的返回电流在平面中的重叠程度也就更大。
10.根据经验法则,当信号线与返回路径平面之间的距离大于等于两条信号线外边缘之间的跨度时,返回路径平面内的电流相互重叠,返回路径平面的存在对信号线的差分阻抗没有影响,此时对差分信号而言,一条信号线的返回电流完全可以看成由另一条信号线运送。
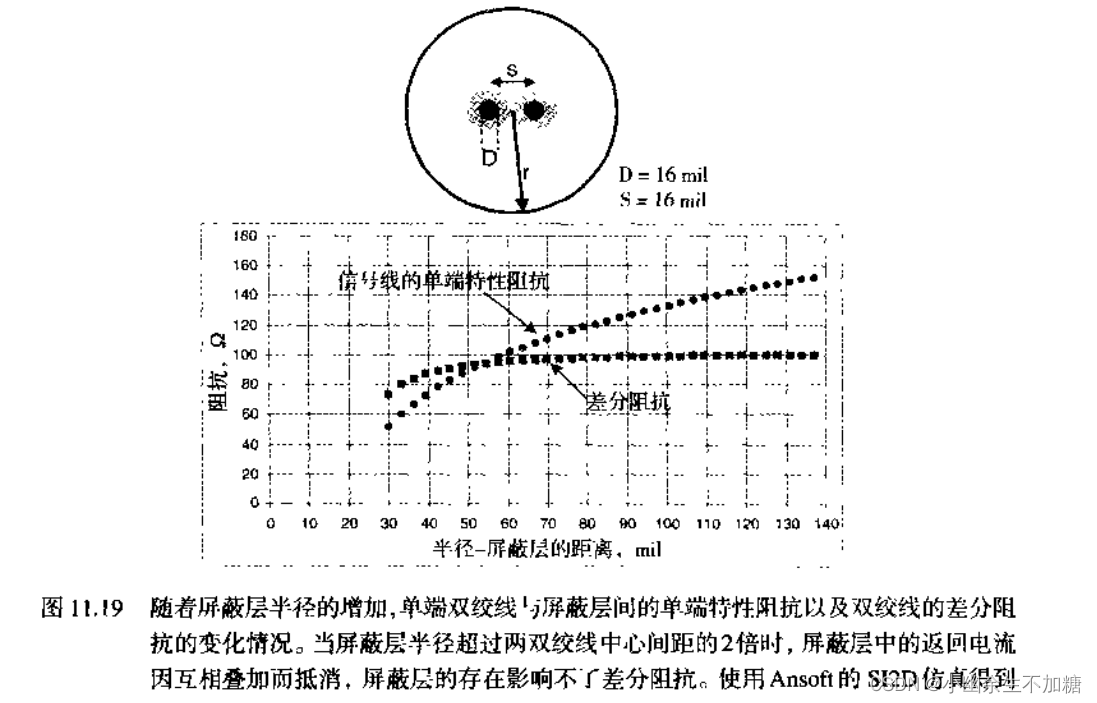
11.(1)当信号线与返回平面之间的耦合度大于两条信号之间的耦合度时,返回路径中出现明显的返回电流,平面在确定差分对差分阻抗时起到了重要作用;
(2)当两条信号线之间的耦合度远大于信号与返回平面之间的耦合度时,平面中的大部分返回电流会叠加抵消掉,平面不影响差分信号,将它移走也不影响到差分阻抗。
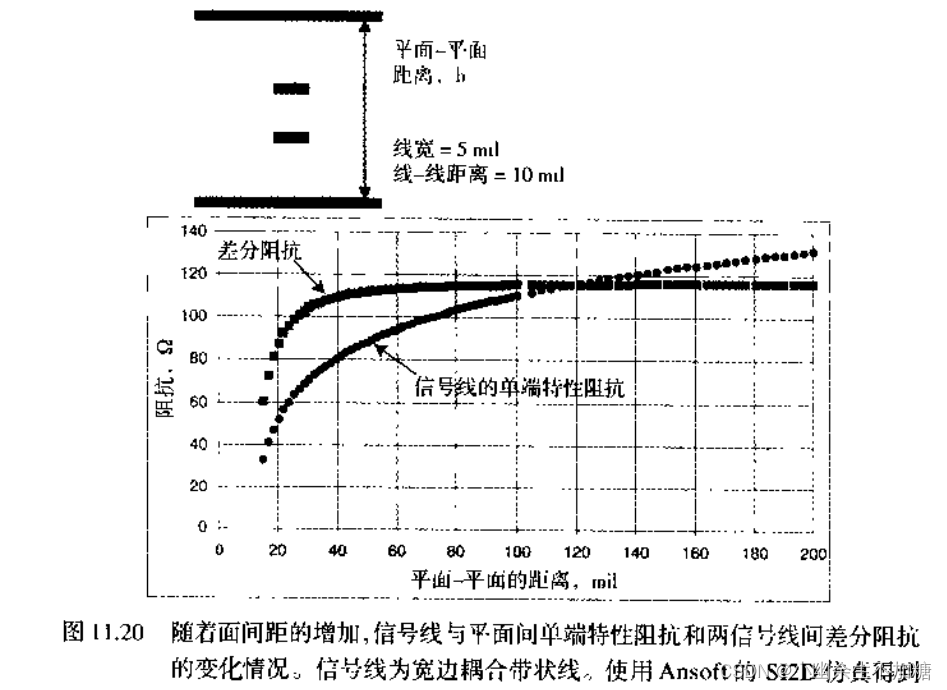
12.经验法则,要使两条信号线之间的耦合度大于信号信号线与返回平面之间的耦合度,则信号线与最近平面之间的距离必须大于两条信号线间距的2倍。