求字符串中循环子串的长度 ← KMP算法

【题目来源】
改编自：https://www.luogu.com.cn/problem/P4391

【问题描述】
给你一个字符串 s1​，它是由某个字符串 s2​ 不断自我连接形成的。但是字符串 s2​ 是不确定的，现在只想知道它的最短长度是多少。

【输入格式】
仅一行，表示输入字符串 s1​ 的一个子串。

【输出格式】
仅一行，表示 s2​ 的最短长度。

【说明/提示】
样例cabcabca的解释：对于样例，我们可以利用abc不断自我连接得到abcabcabc，读入的cabcabca是它的子串。

【规模与约定】
对于全部的测试点，保证字符串的长度 ≤10^6 。

【算法分析】
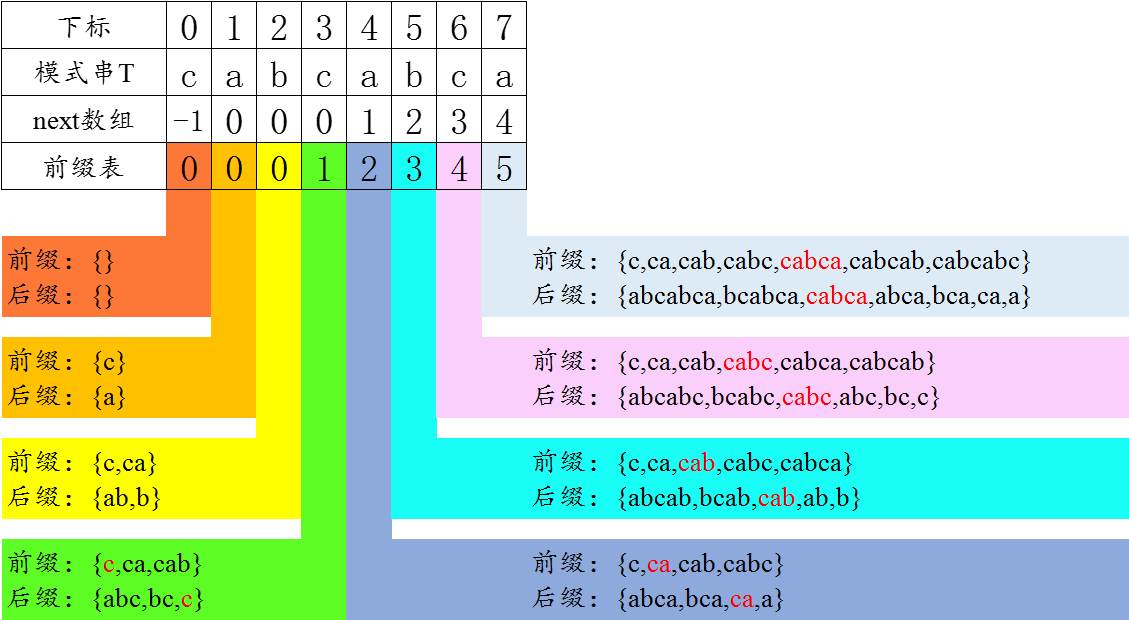
首先要注意，本题输入的字符串比较特殊，是由某个字符串不断自我连接构成的某个字符串的子串。在这个基础上，绘制样例 cabcabca 的前缀表及next数组如下文示意图所示。
由 https://blog.csdn.net/hnjzsyjyj/article/details/127171330 知，前缀表与next数组虽然是有关系的，但是它们不是一回事。且next数组可通过“将前缀表每一位都向右移动1位（最右位舍去）并在最左位补一个-1”得到。
观察示意图可知，循环子串的长度为：T.length()-ne[T.length()]

 
【算法代码】

#include<iostream>
using namespace std;
 
const int maxn=100;
int ne[maxn];
 
void getNext(string T) {
	int len=T.length();
	int i=0, j=-1;
	ne[0]=-1;
	while(i<len) {
		if(j==-1 || T[i]==T[j]) {
			ne[++i]=++j;
		} else j=ne[j];
	}
}
 
int main() {
	string T;
	getline(cin,T);
	getNext(T);
	cout<<(T.length()-ne[T.length()]);
 
	return 0;
}
 
 
/*
in1: cabcabca
out1: 3

in2: ac@# ac@# ac@# 
out2: 5
*/

【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/127112363
https://blog.csdn.net/hnjzsyjyj/article/details/127086502
https://blog.csdn.net/hnjzsyjyj/article/details/127105603
https://www.luogu.com.cn/problem/solution/P4391
https://www.luogu.com.cn/problem/P4391
https://blog.csdn.net/hnjzsyjyj/article/details/120330090