matlab条形图添加误差线_带误差线的条形图

5985811803d9efab59b52320670ad991.gif

误差线可以反应数据有多精确，或者说，(无误差)真实值与观察值之间的距离有多远。对于条形图而言，如果图形反应的是综合的结果(如均值等)，就可能需要添加误差线。本文将对此进行展示。

为了画出带误差线的条形图，我们需要先画出一个条形图。然后，或使用ggplot2中的geom_errorbar()添加误差线。

geom_errorbar()函数需要设定三个参数：

  • ymin 和ymax错误线的底部和顶部的位置

  • x：在x轴上的位置

现假设对于同一变量，有5组被试得分如下：

library(ggplot2)# 创建数据data   name=letters[1:5],  value=sample(seq(4,15),5),  sd=c(1,0.2,3,2,4))data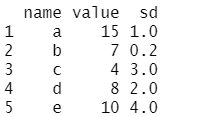

1ad19be86b4bc2a11c2d3bd80fa5aabe.png

共有5组平均值及其标准差

画出带误差线的条形图

ggplot(data) +  geom_bar( aes(x=name, y=value), stat="identity",             fill="skyblue", alpha=0.7) +  geom_errorbar( aes(x=name, ymin=value-sd, ymax=value+sd),                 width=0.4, colour="orange", alpha=0.9, size=1.3)

‍

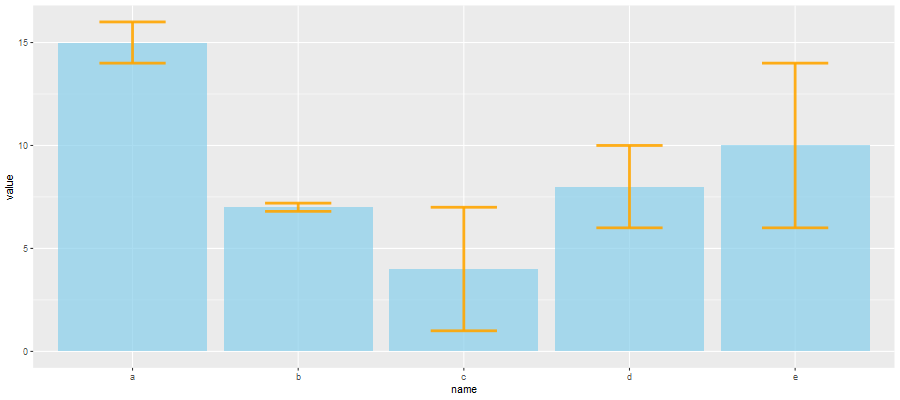
260a6a2b8d86984191da45a3f8ac8113.png

此外，还可以使用：

geom_crossbar()：用于绘制箱形的误差线

ggplot(data) +  geom_bar( aes(x=name, y=value), stat="identity",             fill="skyblue", alpha=0.5) +  geom_crossbar( aes(x=name, y=value, ymin=value-sd, ymax=value+sd),                  width=0.4, colour="orange", alpha=0.9, size=1.3)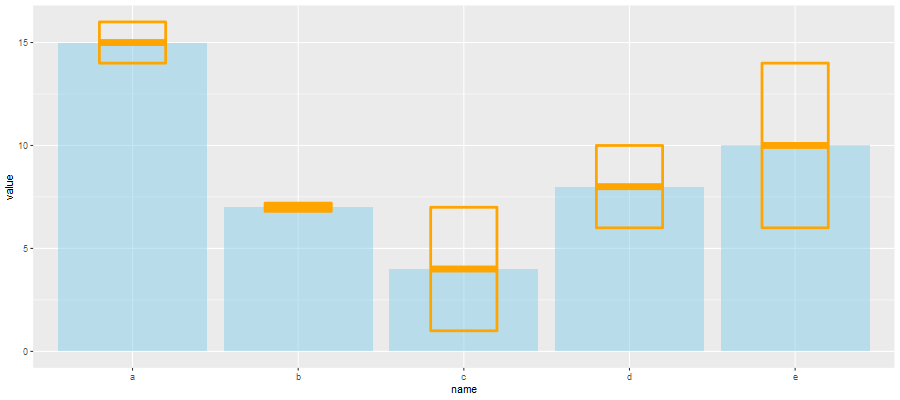

fb7ec7cc71e8b90314f22abe6047e69c.png

geom_linerange()：用于绘制直线形的误差线

ggplot(data) +  geom_bar( aes(x=name, y=value), stat="identity",             fill="skyblue", alpha=0.5) +  geom_linerange( aes(x=name, ymin=value-sd, ymax=value+sd),                   colour="orange", alpha=0.9, size=1.3)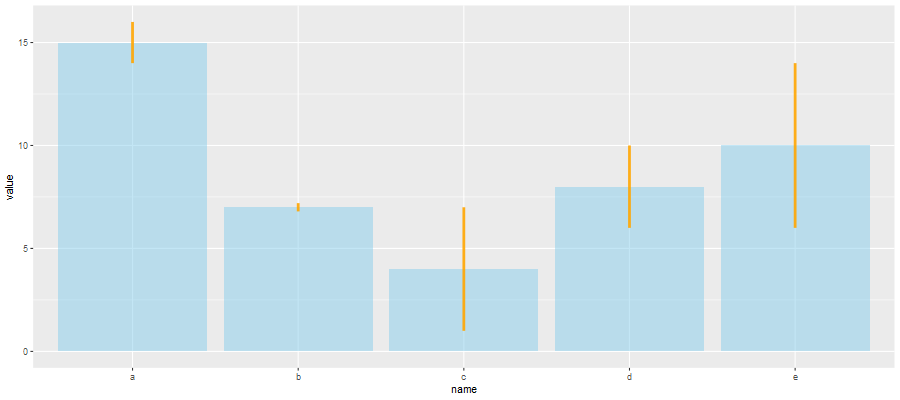

da42a46669d4818f493d5111605aae67.png

geom_pointrange()：用于绘制带点的误差线

ggplot(data) +  geom_bar( aes(x=name, y=value), stat="identity",             fill="skyblue", alpha=0.5) +  geom_pointrange( aes(x=name, y=value, ymin=value-sd, ymax=value+sd),                    colour="orange", alpha=0.9, size=1.3)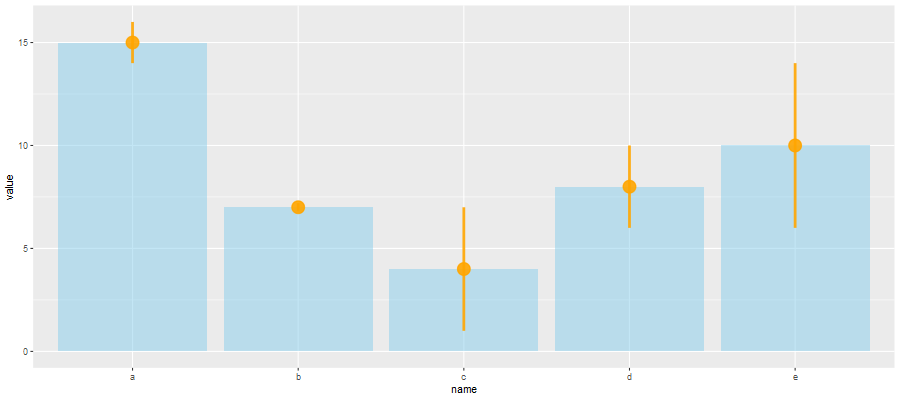

3cbe9cde4dac603f0218e116fee8bff4.png

还可以使用coord_flip()将坐标轴转动90度

ggplot(data) +  geom_bar( aes(x=name, y=value), stat="identity",             fill="skyblue", alpha=0.5) +  geom_errorbar( aes(x=name, ymin=value-sd, ymax=value+sd),                  width=0.4, colour="orange", alpha=0.9, size=1.3) +  coord_flip()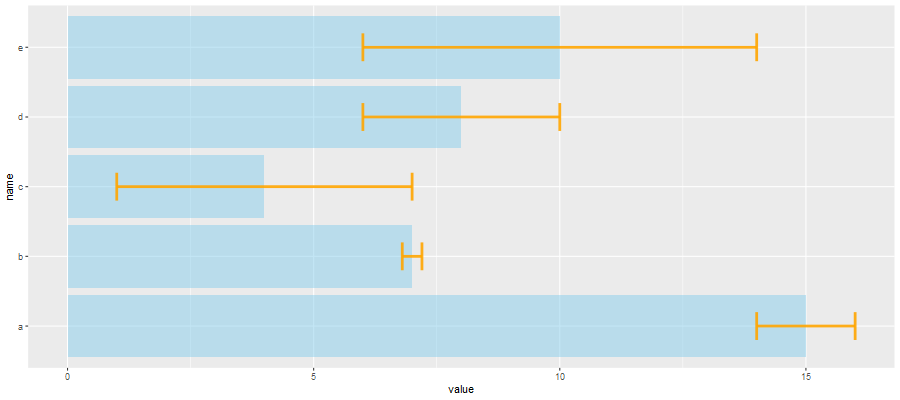

963b26d97c2ad5e782d8614067d799e0.png

上述的图形，我们是用的标准差来画误差线。 实际上，大多数情况下，应该使用置信区间来添加误差线。

置信区间被定义为在一个特定的概率值时数据在平均数之间的波动范围。如果样本容量较大或分布不正态，则最好使用bootstrap方法计算CI。

## 对于一个变量vec,其标准误为se = sd(vec) / sqrt(length(vec))## 对于ci则有alpha = 0.05t = qt((1-alpha)/2 + .5, length(vec)-1)  ## t分布函数lowCI = mean(vec) - t*sehighCI = mean(vec) + t*se## 因此，写一个关于CI的函数CI   se = sd(vec) / sqrt(length(vec))  alpha = 0.05  t = qt((1-alpha)/2 + .5, length(vec)-1)   ci = t*se  return(ci)}

下面将多组条形图与带CI误差线同时呈现。

df   gender = rep(c("M", "F"), 3),  grade = rep(c("7th", "8th", "9th"), each = 2),  a1 = c(1.1, 2.2, 3.1, 4.1, 5.0, 6.1),  a2 = c(1.0, 2.0, 3.2, 4.0, 5.2, 6.0),  a3 = c(1.2, 2.2, 3.2, 4.2, 5.2, 6.2),  a4 = c(0.9, 1.9, 2.9, 3.8, 4.9, 5.4),  a5 = c(1.0, 2.0, 3.0, 4.0, 5.2, 6.0),  a6 = c(1.1, 2.1, 3.1, 4.1, 5.2, 6.1))df1 %   select_if(is.numeric) %>%   mutate(mean = rowSums(.)/6,         ci = apply(., 1, CI),         lowm = mean - ci,         highm = mean + ci)df %   select(-(a1:a6)) %>%   bind_cols(df)    ggplot(df, aes(x=grade, y=mean, fill=gender)) +  geom_bar(position=position_dodge(), stat="identity", colour='black') +  geom_errorbar(aes(ymin=lowm, ymax=highm), width=.2,position=position_dodge(.9))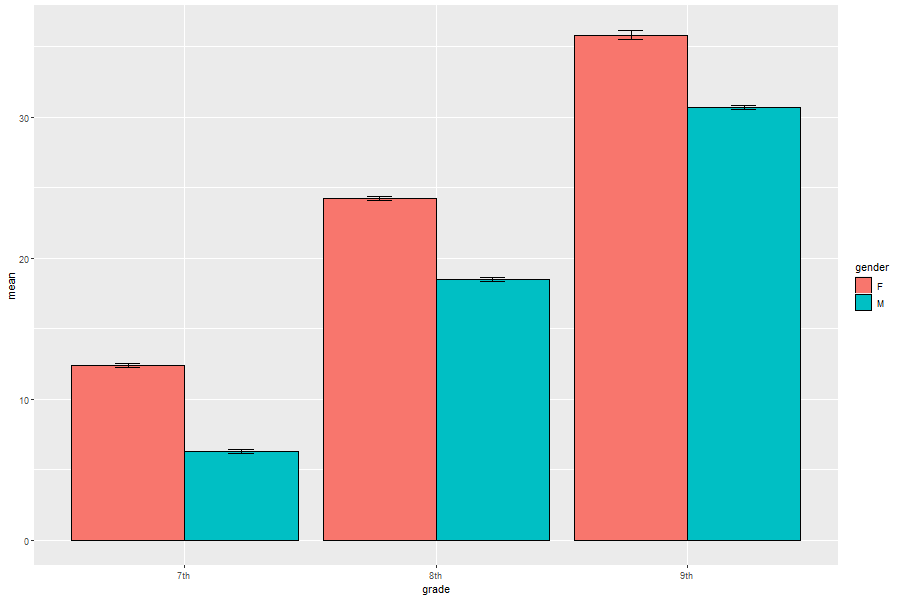

1a03bd79ab0afde8dc08a6505793fa2a.png

404a03eb0861aa2278ecd5fbe29da07b.png

0a204c427daf1170d6ccbfb2f22e0da9.gif

网络分析模型及其实现

多项式加工树模型在心理学中的应用

回归系数的可视化

710b16db074f58c85c6946caa30c8420.png