自变量向量的函数的泰勒公式_向量自变量的线性函数

自变量向量的函数的泰勒公式

数据科学与机器学习的线性代数 (LINEAR ALGEBRA FOR DATA SCIENCE AND MACHINE LEARNING)

In mathematical analysis, one studies functions of any number of variables. Such functions can be regarded as vector functions.

在数学分析中，人们研究许多变量的函数。 这样的函数可以被视为向量函数。

Linear vector functions, also known as linear operators, are of great importance in linear algebra and it’s applications.

线性向量函数，也称为线性算子，在线性代数及其应用中非常重要。

线性形式 (Linear forms)

A numerical function L(x) of a vector argument x, defined on a linear space K over a number field K, is called a linear form if it satisfies the following conditions:

如果满足以下条件，则在数字字段K上的线性空间K上定义的矢量自变量x的数值函数L(x)称为线性形式：

  • L(x+y) = L(x) + L(y) for every x,y ϵ K.

    每x，y ϵ K L(x + y)= L(x)+ L(y)

  • L(αx) = αL(x) for every x ϵ K and every α ϵ K.

    每个x ϵ K和每个αϵ K L(αx)= αL(x) 。

We can write down the general representation of a linear form L(x) defined on an n-dimensional space K_n. Let e1, e2, … , en be and arbitrary basis of the space know, and denote the quantity L(e_k) by l_k (k = 1,2,…,n). Then, given any

我们可以写下在n维空间K_n上定义的线性形式L(x)的一般表示。 令e1，e2，…，en是空间的任意基础，并用l_k(k = 1,2，…，n)表示数量L(e_k ) 。 然后，给定

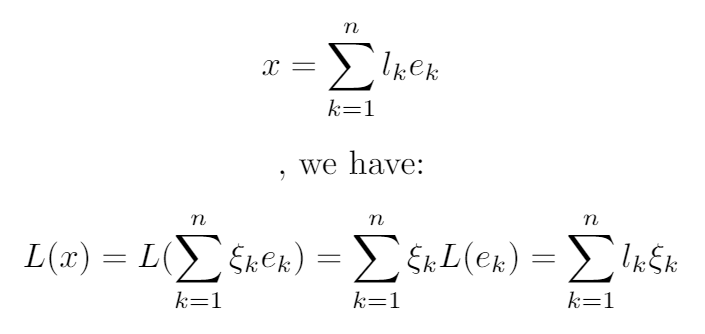
Image for post
Linear form representation, self-generated.
线性形式表示，自生成。

线性算子 (Linear operators)

A morphism A = A(x) of a linear space X is another linear space Y over the same filed k. A(x), also called linear operator maps X into Y. Morphisms should satisfy the following conditions:

线性空间X的射态A = A(x)是相同字段k上的另一个线性空间Y。 A(x) ，也称为线性算子，将X映射为Y。 形态应满足以下条件：

  • A(x+y) = Ax + Ay for every x,y ϵ K.

    每个x，y) K的 A(x + y)= Ax + Ay 。

  • A(αx) = αAx for every x ϵ X and every α ϵ K.

    对于每个x ϵ X和每个αϵ K A(αx)= αAx 。

使用多个线性运算符 (Working with multiple linear operators)

To work with linear operators we should know how we can use them in equations, here are the basic operator rules:

要使用线性算子，我们应该知道如何在方程式中使用它们，这是基本的算子规则：

加成 (Addition)

  • (A+B)x = Ax + Bx

    (A + B)x = Ax + Bx

  • A + B = B + A

    A + B = B + A

  • A+(-A) = 0

    A +(-A)= 0

  • A + 0 = A

    A + 0 = A

乘以数字 (Multiplication by a number)

  • (λA)x = λ(Ax)

    (λA)x =λ(Ax)

  • 1 A = A

    1 A = A

  • (λ1 + λ2)A = λ1 A + λ2A

    (λ1+λ2)A =λ1A +λ2A

  • λ(A+B) = λA + λB

    λ(A + B)=λA+λB

运算符之间的乘法 (Multiplication between operators)

  • (BA)x = B(Ax)

    (BA)x = B(Ax)

  • λ(BA) = (λB)A

    λ(BA)=(λB)A

  • (A+B)C = AC + BC

    (A + B)C = AC + BC

  • (AB)C = A(BC)

    (AB)C = A(BC)

换位 (Transposition)

  • (A’)’ = A

    (A')'= A

  • (A+B)’ = A’ + B’

    (A + B)'= A'+ B'

  • (AB)’ = B’A’

    (AB)'= B'A'

  • (ABC)’ = C’B’A’

    (ABC)'= C'B'A'

逆 (Inverse)

  • AI = IA = A

    AI = IA = A

  • AA^-1 = A^-1A = I

    AA ^ -1 = A ^ -1A = I

  • (A^-1)^-1 = A

    (A ^ -1)^-1 = A

  • (AB)^-1 = B^-1 A^-1

    (AB)^-1 = B ^ -1 A ^ -1

  • (ABC)^-1 = C^-1B^-1A^-1

    (ABC)^-1 = C ^ -1B ^ -1A ^ -1

  • (A’)^-1 = (A^-1)’

    (A')^-1 =(A ^ -1)'

摘要 (Summary)

In this post, we introduced linear operators and the properties that allow us to do math with them, now we know how to work with matrices alone, between matrices and between matrices and numbers. This will be at every formula of machine learning models since OLS(Ordinary least squares) to Deep learning models as GPT-3.

在这篇文章中，我们介绍了线性运算符和使我们可以对它们进行数学运算的属性，现在我们知道了如何单独使用矩阵，在矩阵之间以及在矩阵和数字之间进行运算。 从OLS(普通最小二乘法)到深度学习模型GPT-3，这将是机器学习模型的所有公式。

This is the nineteenth post of my particular #100daysofML, I will be publishing the advances of this challenge at GitHub, Twitter, and Medium (Adrià Serra).

这是我特别＃100daysofML第十九后，我会发布在GitHub上，Twitter和中型企业(这一挑战的进步阿德里亚塞拉 )。

https://twitter.com/CrunchyML

https://twitter.com/CrunchyML

https://github.com/CrunchyPistacho/100DaysOfML

https://github.com/CrunchyPistacho/100DaysOfML

翻译自: https://medium.com/ai-in-plain-english/linear-functions-of-vector-arguments-784b69037ca3

自变量向量的函数的泰勒公式