图像处理小知识点整理一

1.傅立叶变换与小波变换

傅立叶变换是将信号完全的放在频率域中分析，但无法给出信号在每一个时间点的变化情况，并且对时间轴上任何点的突变都会影响整个频率的信号。

傅立叶变换的基是不同频率的正弦曲线，所以傅立叶变换是把信号波分解成不同频率的正弦波的叠加和，不能有效代表突然的变化。

小波变换是以某些特定的函数为基（不止是一个），将数据信号展开成级数系列，它是时间和频率的局部变换，可同时在时域和频率中对数据进行多尺度联合分析，具有多尺度细化分析的功能。因此，我们可以在不同的分解层上和不同的小波基函数对信号进行有效的分析。

小波，不严格的说即有限持续时间的波形，其平均值为零。小波变换就是把一个信号分解成一系列的小波，小波有不同的大小和形状，多种小波的可用性是小波分析的关键优势。

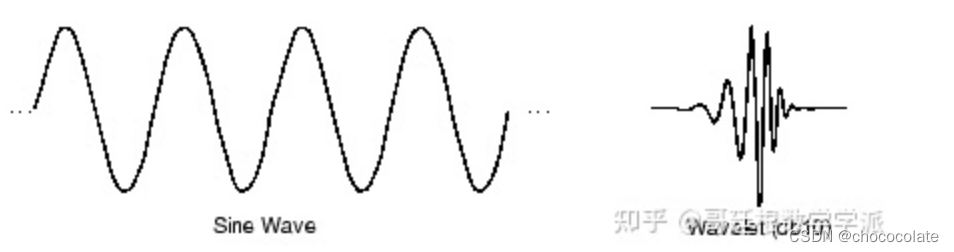
将小波与正弦波进行比较，正弦波是傅里叶分析的基础，正弦曲线的持续时间没有限制—负无穷延伸到正无穷。正弦曲线是平滑的，小波往往是不规则和不对称的。

scaling & shifting

缩放：拉伸或收缩信号

小波在频域中具有带通特性 center frequnecy，拉伸小波有助于捕获信号中缓慢变化的变化，压缩小波有助于捕捉突变。

shifting移动

移动小波只是意味着沿信号长度延迟或推进小波的开始。

小波分析中的两个主要变换是连续与离散小波变换。

CWT(continuous wavelet transform)连续小波变换的关键应用是时频分析和时域频率成分滤波；

DWT(discrete wavelet transform)离散小波变的关键应用是信号和图像的去噪和压缩，因为它有助于表示许多自然产生的信号和具有较少系数的图像。

上采样

放大图像（或者称为上采样upsampling或者图像插值interpolating）的主要目的是放大原图像，从而可以使图像在更高的显示设备上。图像放大几乎是采用内插值方法，即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。

下采样

缩小图像（或称为下采样subsampling或者降采样downsampled）的主要目的有两个：

1.使得图像符合显示区域的大小；

2.生成对应图像的缩略图。

对图像的缩放操作并不能带来更多关于该图像的信息，因此图像的质量将不可避免受到影响。然而，确实有些缩放方法能够增强图像的信息，从而使得缩放后的图像质量超过原图质量。

对于一幅尺度为M*N，对其进行s倍下采样，即得到（M/s)*(N/s)尺寸的图像（s应该是M和N的公约数）。如果该图像是矩阵形式，则其本质上是将原始图像s*s窗口内的图像变成一个像素点，该像素点的值为该窗口内所有像素的均值。

这位博主讲解的很详细了，就不自己整理了，指路⬇️：