【路径规划-机器人栅格地图】基于哈里斯鹰算法求解栅格地图路径规划及避障含Matlab源码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机

⛄ 内容介绍

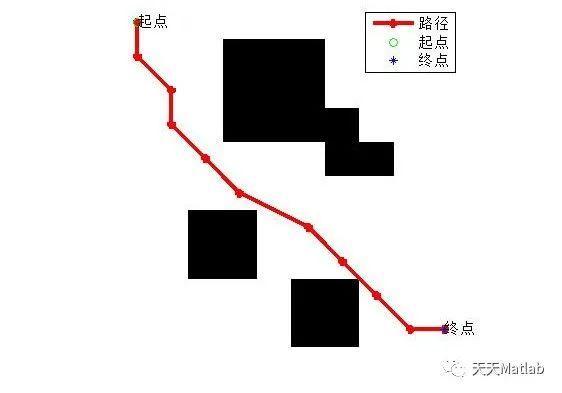
静态环境中的移动机器人全局路径规划是路径规划中的一个重要问题,本文采用哈里斯鹰解决移动机器人的路径规划.该方法首先采用栅格法环境建模,采用哈里斯鹰算法规划机器人路径,最后用MAT-LAB来实现算法,仿真后,观察路径,得出最终结果.

⛄ 部分代码

function [BestFitness, gbest, zz] = GWO(N, maxgen, X, fitness, lb, ub, dim, fobj)

%% 

[bestfitness, bestindex] = sort(fitness);

gbest = X(bestindex(1), :);      % 群体最优极值

fitnessgbest = bestfitness(1);             % 种群最优适应度值

% 初始化alpha, beta和delta_pos

Alpha_pos = gbest;

Alpha_score = fitnessgbest; 

Beta_pos = X(bestindex(2), :);

Beta_score = bestfitness(2); 

Delta_pos = X(bestindex(3), :);

Delta_score = bestfitness(3); 

%% 初始结果显示

disp(['初始位置：', num2str(gbest)]);

disp(['初始解：', num2str(fitnessgbest)]);

%% 迭代

for gen = 1:maxgen

%     a = aini-(aini-afin)*exp(gen/maxgen-1);     % a从2线性减小到0    

%      a = ainitial/(1+exp(mu*gen/maxgen-k));

     a=2-gen*(2/maxgen);     % a从2线性减小到0    

    % 更新包括omegas在内的种群的位置

    for i = 1:N

        S = X(i, :);

        for j = 1:dim

            r1 = rand();             % r1是[0,1]中的随机数

            r2 = rand();             % r2是[0,1]中的随机数

            A1 = 2*a*r1-a;        % 公式（4）

            C1 = 2*r2;               % 公式（5）

            D_alpha = abs(C1*Alpha_pos(j)-X(i, j));  % 公式（6）-第一部分

            X1 = Alpha_pos(j)-A1*D_alpha;   % 公式 (7)-第一部分

            

            r1 = rand();

            r2 = rand();

            A2 = 2*a*r1-a;         % 公式（4）

            C2 = 2*r2;                % 公式（5）

            D_beta = abs(C2*Beta_pos(j)-X(i, j));   % 公式（6）-第二部分

            X2 = Beta_pos(j)-A2*D_beta;       % 公式 (7)-第二部分

            

            r1 = rand();

            r2 = rand();

            A3 = 2*a*r1-a;        % 公式 (4)

            C3 = 2*r2;               % 公式 (5)

            D_delta = abs(C3*Delta_pos(j)-X(i, j)); % 公式（6）-第三部分

            X3 = Delta_pos(j)-A3*D_delta;      % 公式 (7)-第三部分

            

            X(i, j)=(X1+X2+X3)/3;       % 公式 (8)

        end

        % 边界处理

        X(i, X(i, :) > ub) = ub;

        X(i, X(i, :) < lb) = lb;

        % 判断

        fit = fobj(X(i, :));

        if fit < fitness(i)

            fitness(i) = fit;

        else

            X(i, :) = S;

        end

    end

    % 更新

    [bestfitness, bestindex] = sort(fitness);

    gbest = X(bestindex(1), :);           % 群体最优极值

    fitnessgbest = bestfitness(1);      % 种群最优适应度值

    % 初始化alpha, beta和delta_pos

    Alpha_pos = gbest;

    Alpha_score = fitnessgbest;

    Beta_pos = X(bestindex(2), :);

    Beta_score = bestfitness(2);

    Delta_pos = X(bestindex(3), :);

    Delta_score = bestfitness(3);

   

    %% 每一代群体最优值存入zz数组

    zz(gen) = Alpha_score;

    gbest = Alpha_pos;

    %% 显示每代优化结果

    display(['At iteration ', num2str(gen), ' the best fitness is ', num2str(zz(gen))]);

end

BestFitness = zz(end);

%% 最终结果显示

disp(['最优位置：', num2str(gbest)]);

disp(['最优解：', num2str(zz(end))]);

% %% 绘图

% figure;

% plot(zz, 'r', 'lineWidth', 2);          %  画出迭代图

% xlabel('迭代次数', 'fontsize', 12);

% ylabel('目标函数值', 'fontsize', 12);

⛄ 运行结果

⛄ 参考文献

[1]张涛, 张震. 基于混合算法的安防巡检机器人避障路径规划[J]. 电子测量技术, 2020, 43(13):5.

❤️ 关注我领取海量matlab电子书和数学建模资料

❤️部分理论引用网络文献，若有侵权联系博主删除