sklearn-5模型评估与改进
通过前述章节可以发现,可调用模型的.score方法获取测试集评分,还有其他方法可以更好的评估模型,有交叉验证和网格搜索
1 交叉验证
特点 1数据被多次划分,且需要训练多个模型
k折交叉验证 k由用户指定,通常取5-10, 将数据均分为k份,每份叫做折,然后开始训练数据,训练k次,每第k次训练时,取第k折数据作为测试集,其他数据均为训练集,最后可以得到k个模型训练的打分,一般可以用k次训练的平均值作为交叉验证的结果
1.1 优缺点
优点
1 验证次数多,验证均匀,不会像train_test_split一样,可能偶尔某个测试集异常数据较多,导致测试结果不稳定
2 训练集比例不同。RFE训练数据比例高于train_test_split的划分比例(75%)
缺点
1 交叉验证多次训练,更消耗时间,大约比单次训练验证慢k倍
2 交叉验证只是验证,不会返回经过数据训练的数据模型,只能获取得分
1.2 k折交叉验证和其他策略
1.2.1 分层k折交叉验证
分层k折和一般k折不同点在于,一般k折直接按顺序k分支一取测试集,如果原始数据分布不均匀,k折会不太稳定,一种解决方法是分层k折。分层k折是保证每个测试集和训练集的分类的百分比占比都为k分之一。cross_val_score默认使用的k折是一般k折交叉验证
1.2.2 交叉验证分离器
可将一些参数传给交叉分离器,交叉分离器可作为cv参数传入,类似于一种解耦
默认使用3折交叉验证iris时效率为0,因为数据已经有序分为3类,所以每次训练集都是一样的,只有一个种类,就啥也学不到
1.2.2.1 默认k折分离器
def test_cross_kfold(self):
kfold = KFold(n_splits=5)
logreg = LogisticRegression().fit(self.iris.data, self.iris.target)
print(f'5 fold cross score: {cross_val_score(logreg, self.iris.data, self.iris.target, cv=kfold)}')
print(f'3 fold cross score: {cross_val_score(logreg, self.iris.data, self.iris.target, cv=KFold(n_splits=3))}')
1.2.2.2 留一法交叉验证
概念 每次k折保留单个样本(集测试集只有一个样本)
优点 适合小型数据集,准确度高
缺点 耗时,需很多次模型创建与训练
def test_cross_leave_one(self):
loo = LeaveOneOut()
logreg = LogisticRegression().fit(self.iris.data, self.iris.target)
scores = cross_val_score(logreg, self.iris.data, self.iris.target, cv=loo)
print(f'score number: {len(scores)}, score mean: {scores.mean()}')
1.2.2.3 打乱划分交叉验证
随机从数据集取数据作为测试集和训练集,这俩没有交集,且可以不用把所有数据取完,可以取一部分
def test_cross_shuffle_split(self):
logreg = LogisticRegression().fit(self.iris.data, self.iris.target)
shuffle_split = ShuffleSplit(test_size=.5, train_size=.5, n_splits=10)
scores = cross_val_score(logreg, self.iris.data, self.iris.target, cv=shuffle_split)
print(f'shuffle split scores: {scores}')
1.2.2.4 分组交叉验证
例子 从已知人脸的情感识别出新人脸的感情,target是情感。对机器模型来说,学习出现过的人脸情感比新人脸的情感容易,因此希望训练集和测试集不包含相同的人的人脸,可以用分组交叉验证
分组交叉验证按照groups输入参数将输入分成不同组,每次验证将一个组的数据作为测试集,如果组不够则将剩下的数据作为测试集,其他说句作为训练集

def test_cross_group_split(self):
groups = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
scores = cross_val_score(LogisticRegression(), *self.blob, groups=groups, cv=GroupKFold(n_splits=4))
print(f'cross validation scores: {scores}')![]()
2 网格搜索
概念 网格搜索是一种调参的方法,类似于笛卡尔积的概念,将所有不同类参数的所有结果都组合在一起看性能,找出一组性能最佳的参数组合
2.1 简单网格搜索
就是网格搜索的概念,比如核svm有两个参数核半径和正则化参数,可以用两个for循环遍历要取的值,循环体内保留最高精度和对应的参数值,最后输出.不需要从sklearn导入其他模块
2.2 参数过拟合风险和验证集
验证集 训练集用来训练模型,测试集用来调参,找出最优参数,最优参数是否足够优秀,需要用新的数据去检验,而不应该用训练集和用来调参的测试集。为解决此问题,可以在训练模型前将原始数据集分成三部分,训练集,测试集,验证集。验证集就是用来校验模型调参结果的数据。如果用调参的测试集去验证模型准确度,会发现实际准确度达不到,因为测试集已经用过了,再用会过拟合导致高准度但泛化能力低
如何获取验证集 可以调用两次train_test_split
2.3 交叉验证+网格搜索(GridSearchCV)
网格搜索是选出最优参数,而交叉验证可以很好的验证参数泛化能力,其实可以用交叉验证替代验证集,且验证集对划分方案很敏感,不太合适
特点 1 交叉验证+网格搜索会导致计算量大,耗时 2 相比于手动交叉+网格,免去了划分验证集工序,模型直接用训练集做模型训练和参数评分,最后用测试集验证泛化能力
sklearn支持 交叉验证+网格搜索,sklearn提供了一体化模块,免去了手动for调多个参数然后交叉验证的繁琐。sklearn使用sklearn.model_selection.GridSearchCV实现,逻辑是先网格+交叉验证找到最优参数,然后最终评估。训练,测试数据和参数列表需要手动传参。看个例子
性质 1 网格找到的最佳参数存在模型的best_params_字段中 2 交叉验证的最高得分存在模型的best_score_字段中 3 模型所有字段存在模型的best_estimator_字段中
def test_grid_and_cross(self):
params = {'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid_search = GridSearchCV(SVC(), params, cv=5)
xtr, xte, ytr, yte = train_test_split(self.iris.data, self.iris.target, random_state=0)
grid_search.fit(xtr, ytr)
print(f'test grid search score: {grid_search.score(xte, yte)}')
print(f'test grid search best params: {grid_search.best_params_}')
print(f'test grid search best scores: {grid_search.best_score_}')
print(f'test grid search best all params: {grid_search.best_estimator_}')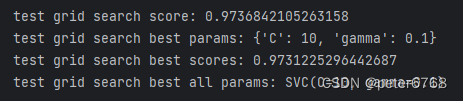
2.3.1 分析交叉验证结果
因为网格调参会比较多,此节用可视化方法分析
网格搜索的结果存在cv_results_字段,保存了每个网格的参数和训练得分
可视化方法为热图
def test_visualization_cross_and_grid(self):
params = {'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid_search = GridSearchCV(SVC(), params, cv=5)
xtr, xte, ytr, yte = train_test_split(self.iris.data, self.iris.target, random_state=0)
grid_search.fit(xtr, ytr)
scores = np.array(pd.DataFrame(grid_search.cv_results_).mean_test_score).reshape(6, 6)
mglearn.tools.heatmap(scores, xlabel='gamma', xticklabels=params['gamma'], ylabel='C', yticklabels=params['C'], cmap='viridis')
plot.show()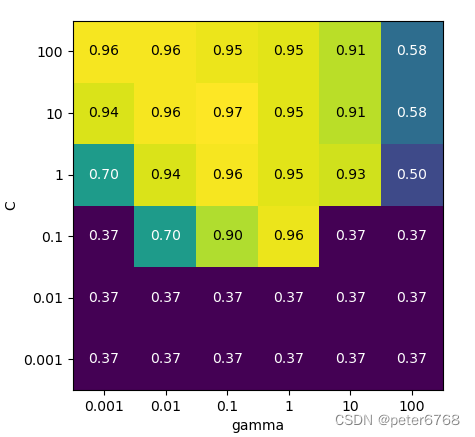
2.3.2 在非网格 空间中搜索
问题 有时候参数组合会动态变化,比如SVC的kernel类别,如果是线性kernel则不用gamma,如果kernel是rbf则C和gamma都要用,如果在线性kernel时网格搜索gamma和C,那么C时没意义的。为解决此问题,可以使用GridSearchCV模型的参数param_grid,这个和params参数不同的是,可以将线性kernel和rbf kernel放在一个列表里,每个列表项是一个字典,键就是C,gamma和kernel类别,用param_grid替代param
可视化 可以通过grid_search.cv_results_看结果,发现kernel线性的gamma参数为NAN
2.3.3 使用不同交叉验证策略进行网格搜索
GridSearchCV也可以使用不同的交叉验证方法
GridSearchCV对分类问题默认使用分层k折,对回归问题默认使用一般k折
实现 构造不同的验证分离器,作为cv参数传给GridSearchCV即可
存在的必要性 之前的策略是事先划分测试集和训练集,然后交叉验证+网格搜索,缺点是所有验证和网格搜索都依赖于最开始的测试划分,没有验证和网格搜索在测试集上进行,这在某种程度会导致轻微的过拟合,为避免此问题,可以采用嵌套交叉验证,即先用交叉验证将数据划分为测试集和训练集,再用GridSearchCV模型对交叉验证划分的数据交叉验证
def test_nested_cross(self):
params = {'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
scores = cross_val_score(GridSearchCV(SVC(), params, cv=5), self.iris.data, self.iris.target, cv=5)
print(f'nested cross scores: {scores}, \n nested cross mean scores: {scores.mean()}')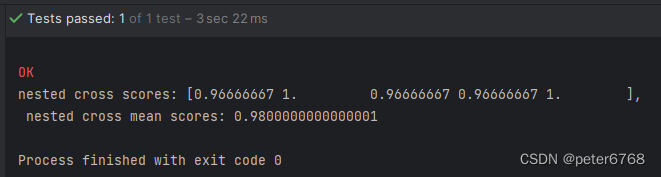
性能 1 嵌套交叉验证构造更多的模型:36*5*5=900个模型,36是一次网格搜索构造的模型数量,第一个5是GridSearchCV网格搜索做的交叉验证,第二个5是5次交叉验证保证每次传给GridSearchCV的测试集不一样,用不一样的测试集去交叉验证 2 虽然次数很多,但交叉验证和网格搜索可以并行,模型的传入参数n_jobs可以控制并行数,参数表示并行数,如果设为-1则表示用主机所有内核 3 注意,并行不能嵌套,即如果GridSearchCV使用了嵌套,那么给GridSearchCV传入的训练模型就不可以用并行,sklearn不支持,但没试过
3 评估指标与评分
目前学到现在,一直都用R平方来评估分类和回归模型的精确度,有的模型并不适用R平方评估模型精确度,有更合适的指标,学习下
3.1 选择目标与商业化
一般机器学习都需要应用到现实生活,模型的好坏取决于在实际生活中发挥的作用,这个通过指标呈现,比如手术机器人手术速度,精确度等,越高说明模型越好,这里的手术速度,精确度就是现实的商业指标,但在开发阶段没有这样的现实环境,可又需要这样的现实指标才能评估模型的好坏,怎么办呢?可以找个近似的指标,学习下一般可以考虑哪些近似的指标
3.2 二分类指标
通过 正类 和 反类 两个概念来描述结果是否为我们想要的,与预期相符即为正类,否则为反类
3.2.1 错误类型
考虑预测癌症病人的性质是阴性还是阳性,此处将阳性结果视为正类
假正例/假反例 比如预测一个人癌症阳还是阴性,比如一个人癌症实际是阴性,但预测错了预测为阳性,这种情况叫假正例。假反例就是反过来
第一类错误/第二类错误 统计学上,假正例也叫第一类错误;假反例也叫第二类错误
回到例子中,第一类错误的影响可能导致患者做多的检查,但第二类错误会导致患者误以为自己是阴性但他实际是阳性,可能错过治疗最佳实际,严重的话甚至威胁生命,所以一般我们在设定正类和反类后,应该尽可能避免假反例(即第二类错误)
当然也可能有的场景第一类错误的影响远大于第二类错误,此时可以重点关注第一类错误
3.2.2 不平衡数据集
比如让三个女孩在10000个男孩里挑选最喜欢的人,男孩被喜欢了标1,男孩没被女孩喜欢标0,然后用男孩是否被标1来评估男孩的魅力程度。最后汇总10000个男孩里每个男孩是否被女孩喜欢的结果,得到的数据点有10000个,其中9997个是0,3个是1,但仅靠3个1很难评估这三个男生是有魅力的,也很难评估9997个男生是没魅力的,这种情况可以看作不平衡数据集的一个例子,而不平衡数据集在生活中更为常见
继续看上面这个例子,比如最后用百分比来看,99.97%的男生都没有被女生喜欢,光看数值发现数值很高,但实际这个数值并不能表示什么,不能表示99.97%的男生都没有魅力,而需要用其他指标去评估10000个男生到底谁有魅力
3.2.3 混淆矩阵
混淆矩阵输出一个2x2的数组,数组的元素是数据集的样本,两个行表示两个实际的类别,两个列表示两个预测的类。主对角线(matrix[i][i])上的数据是正确的(即预测类和实际类一致)。通过混淆矩阵可以看出正确和错误预测的样本
混淆矩阵的四个趋于可以用 假正例(false positive,FP),假反例(false negative, FN),真正例(TP),真反例(TN)来描述
指标预测模型 通过FP,FN,TP,TN可以预测模型准确度,公式为(TP+TN)/(TP+TN+FP+FN)
准确率 公式是TP/(TP+FP),描述预测的正类有多少是真实的正类。如果限制FP的数量,可以考虑用准确率评估模型。比如验证新药是否有药效,在1000个小白是做实验,997个起作用了,3个没起作用,准确率99.7%
召回率/灵敏度/命中率 公式是TP/(TP+FN),描述真实正类中有多少被预测为正类。如果希望TP高,可以使用召回率评估模型。比如在预测的阳性癌症患者中找到真实阳性患者,这很有用
f分数 结合了准确率和召回率,是两者的调和平均,公式是2*(准确率*召回率)/(准确率+召回率)
准确率和召回率都是越高越好,两个要一起看,不能只看一个,比如如果让召回率到100但准确率很低,这可能不太行。(思考为很么两个都要高)
classification_report可以将准确率,召回率,f分数都打印出来
def test_digits_predict_metric(self):
xtr, xte, ytr, yte = train_test_split(self.digits.data, self.digits.target == 9, random_state=0)
dummy = DummyClassifier(strategy='most_frequent').fit(xtr, ytr)
pred_most_freq = dummy.predict(xte)
print(f'{classification_report(yte, pred_most_freq, target_names=["not nine", "nine"])}')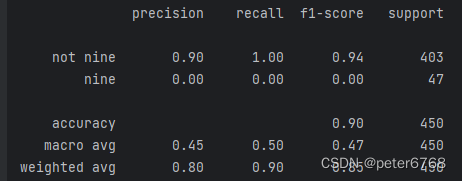
作用 通过混淆矩阵和classification_report可以看到更多指标,可以全面衡量模型准确度
3.2.4 考虑不确定性
可以通过联合classification_report和decision_function和predict_proba调整决策边界获取好的报告(当然要切合实际),predict_proba值域为0-1(概率),更好操作
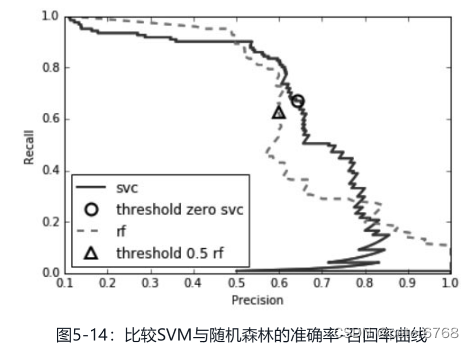
3.2.5 准确率-召回率曲线
概念 即训练一个分类模型,然后画二维图,两个方向分别是准确率和召回率,变量是decision_function的阈值,每取一个阈值,准确率和召回率也会取一个值,将所有decision_function的值对应的准确率和召回率的值绘图,就是准确率-召回率曲线
意义 1 准确率和召回率越大越好,绘图后可根据实际情况取舍,有助于可视化,是对f1分数的补充,因为f1分数看不到准确率和召回率(f1分数只提供了准确率召回率曲线上阈值为0的那个点) 2辅助对比多个模型哪个好,可以此为量化指标
量化 1一种量化指标是取曲线的平均值,即平均准确率(感觉就是算面积,积分或累次相加)
3.2.6 受试者工作特征(ROC)与AUC
概念 类似于准确率-召回率曲线,只是两个坐标代表的东西不一样,换成了假正例率(FP/(FP+TN))和真正例率(TP/(TP+FN)),真正例率同时也是召回率
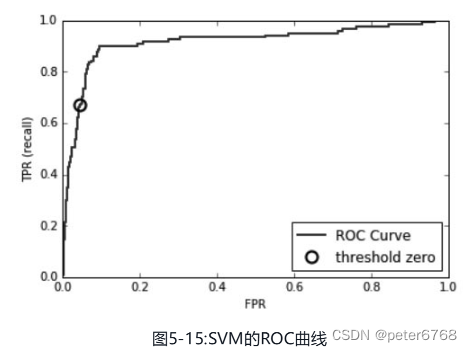
指标意义 越靠近左上角越好,即真正例率越高,假正例率越低,越好
量化 类似于准确率-召回率曲线,也可计算平均值(积分或面积)
意义 1不平衡数据集来说,AUC/ROC是一个很好的指标
注意 AUC没调节阈值,获得了AUC高的组合参数后,一般还要调节阈值进一步
3.3 多分类指标
多分类一般看混淆矩阵和分类报告
多分类报告里有三种汇总值 1macro计算未加权的f分数(无视每个类的样本数) 2weighted计算加权的f分数 3micro计算假正例,假反例,真正例数量,用这些计数计算准确率,召回率,f分数
3.4 回归指标
精度一般够了
3.5 如何使用评估指标
交叉验证和网格搜索 提供了参数输入来选择不同的评估指标比如AUC,参数是scoring="xxx"
分类问题常用指标 accuracy, roc_auc,avg_precision(准确率召回率面积),f1, f1macro,f1micro,f1_weighted
回归问题常用指标 r2, 均方误差,平均绝对误差