梯度消失和梯度爆炸
1. 前向传播和反向传播
在讲解梯度消失和梯度爆炸之前,我们需要先了解什么是前向传播和反向传播。
前向传播: 输入层数据开始从前向后,数据逐步传递至输出层。
反向传播: 损失函数从后向前,梯度逐步传递至第一层。
在讲解前向传播和反向传播计算过程之前,我们先介绍一下计算图的概念,通过计算图可以很清楚的了解后向传播的计算过程,以3层网络为例。
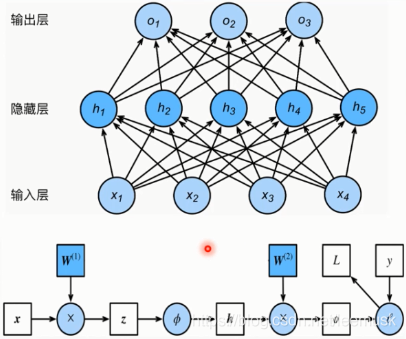
蓝色圆圈表示运算操作,分别为乘法,激活函数,乘法,损失函数;白色框框表示传播的数值;蓝色框框表示权重;
前向传播不同多说,不断的乘以权重在通过激活函数即可;
反向传播的计算过程本质是链式求导过程。下面为
W
1
W_1
W1的计算过程,从后向前逐步进行计算。
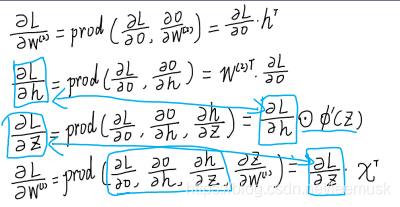
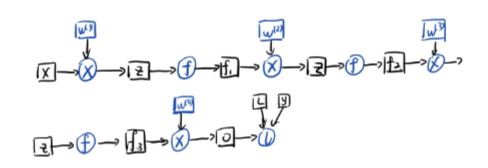
2. 梯度消失和梯度爆炸产生的原因
了解了前向传播和反向传播机制之后,再去了解梯度消失、爆炸就很简单了。
以5层网络为例,激活函数为
f
(
z
)
f(z)
f(z),
f
i
+
1
=
f
(
f
i
⋅
x
)
f_{i+1} = f(f_i \cdot x)
fi+1=f(fi⋅x),通过计算图给出
W
1
W_1
W1的梯度推导公式,我们将根据这个公式进行梯度消失、爆炸的分析。
Δ
W
1
=
∂
l
o
s
s
∂
o
u
t
∂
o
u
t
∂
f
3
∂
f
3
∂
2
∂
f
2
∂
f
1
∂
f
1
∂
W
1
=
∂
l
o
s
s
∂
o
u
t
W
4
f
′
W
3
f
′
W
2
f
′
x
Δ
W
2
=
∂
l
o
s
s
∂
o
u
t
∂
o
u
t
∂
f
3
∂
f
3
∂
f
2
∂
f
2
∂
W
2
=
∂
l
o
s
s
∂
o
u
t
W
4
f
′
W
3
f
′
f
1
\Delta W_1 = \frac {\partial loss} {\partial out} \frac {\partial out} {\partial f3} \frac { \partial f3} {\partial 2} \frac {\partial f2} {\partial f1} \frac {\partial f1} {\partial W_1} \\ \quad \\ = \frac {\partial loss} {\partial out} W_4f'W_3f'W_2f'x \\ \quad \\ \Delta W_2 = \frac {\partial loss} {\partial out} \frac {\partial out} {\partial f3} \frac { \partial f3} {\partial f_2} \frac {\partial f_2} {\partial W_2} \\ \quad \\ = \frac {\partial loss} {\partial out} W_4f' W_3f'f_1
ΔW1=∂out∂loss∂f3∂out∂2∂f3∂f1∂f2∂W1∂f1=∂out∂lossW4f′W3f′W2f′xΔW2=∂out∂loss∂f3∂out∂f2∂f3∂W2∂f2=∂out∂lossW4f′W3f′f1
笔者将梯度消失、爆炸产生原因主要分为两类:
1、权重初始化值设置不当
权重设置的过大,即使乘以 f’ 也大于1,则梯度以指数形式增加,出现梯度爆炸;或者
权值设置的过小,梯度以指数形式减小,出现梯度消失。
2. 数据尺度过大
数据的标准差在前向传播过程中逐层扩大
n
\sqrt{n}
n 倍,若权重初始化设置不当,将造成数据尺度过大,数据为nan,出现梯度爆炸。如
W
2
W_2
W2 的求导公式中,若
f
1
→
∞
f_1 \rightarrow \infty
f1→∞ ,则
Δ
W
2
→
∞
\Delta W_2 \rightarrow \infty
ΔW2→∞
3、激活函数
如果激活函数的导数 f’ 小于1,则以指数级形式衰减,造成梯度消失;若大于1,则以指数形式增加,造成梯度爆炸。在实际情况中,激活函数的值通常小于1,出现梯度消失现象。
总而言之,无论是初始值设置不当还是激活函数导致梯度消失、爆炸,归根结底还有反向传播的连乘造成的。
3. 解决梯度消失、爆炸
3.1 权值初始化
在前向传播过程中,每经过一层网络,标准差就会扩大 n \sqrt{n} n 倍(没有激活函数层),数据尺度以指数形式增加,引发梯度爆炸。为此,提出了方差一致性 定理。
方差一致性: 保持数据尺度在恰当的范围,通常方差为1;
在保持方差一致性的条件上进行权值初始化的方法根据使用的激活函数的变化而变化的。不同的激活函数适用不同的权重初始化方法。
若使用饱和激活函数,如tanh,使用 Xavier 初始化方法
W
∼
U
[
−
6
n
i
+
n
i
+
1
,
6
n
i
+
n
i
+
1
]
W \sim U[-\frac {\sqrt{6}} {\sqrt{n_i + n_{i+1}}}, \frac {\sqrt{6}} {\sqrt{n_i + n_{i+1}}}]
W∼U[−ni+ni+16,ni+ni+16]
若使用非饱和激活函数,relu及其变体,使用 kaiming初始化方法
D
(
W
)
=
2
n
i
D
(
W
)
=
2
(
1
+
a
2
)
n
i
D(W) = \frac 2 {n_i} \\ \quad \\ D(W) = \frac 2 {(1+a^2)n_i}
D(W)=ni2D(W)=(1+a2)ni2
针对不同的激活函数,使用合适的初始化方法可以有效的避免由于数据尺度过大造成的梯度消失、爆炸问题。
3.1.1 初始化的常见问题
-
如果用0初始化所有参数,那么会产生什么后果?
答:所有的神经元都是相同的,参数以相同的方式进行更新 -
使用小的随机数初始化参数,会有什么结果?
答:在浅层网络中正常使用,但在深层网络中会产出问题,所有激活值会变为0, 反向传播时,梯度基本没有更新。 -
使用较大的值初始化权重(使用tanh激活函数)?
答:会造成梯度消失,进入饱和状态
3.2 使用非饱和激活函数
非饱和激活函数如 Relu、Leaky Relu、 Exponential Linear Unit(ELU)
3.2.1. Relu
f
(
x
)
=
m
a
x
(
α
x
,
x
)
f(x) = max( \alpha x, x)
f(x)=max(αx,x)
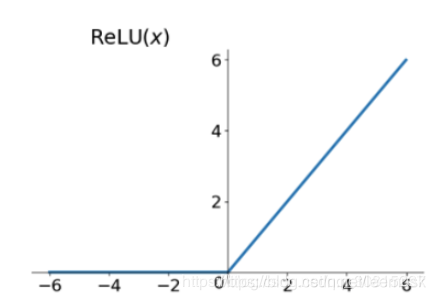
Relu 的优点:
- 解决了饱和问题,减少了梯度消失
- 计算高效
缺点:
- 不是以0为中心
- 存在部分梯度消失,在负半轴
这里我们提一下为什么要有以0为中心。若输出不是以0为中心,会导致梯度沿着同一个方向移动,即呈锯齿状下降,使梯度更新过程低效。
在一次梯度更新的过程中,
w
1
,
w
2
,
.
.
.
w_1, w_2, ...
w1,w2,... 改变的方向是统一的,或正或负。以
Δ
W
2
\Delta W_2
ΔW2的更新过程为例,
∂
l
o
s
s
∂
o
W
4
f
′
W
3
f
′
\frac {\partial loss} {\partial o} W_4f'W_3f'
∂o∂lossW4f′W3f′ 为神经元的误差,在一次反向传播过程中是不变的,
f
i
f_i
fi是上一层神经元的输入,经过激活函数,一定大于0。所以
W
2
W_2
W2 的各分量
w
1
,
w
2
,
.
.
.
w_1, w_2, ...
w1,w2,... 更新方向是统一的。
3.2.2. Leaky Relu
f
(
x
)
=
m
a
x
(
α
x
,
x
)
f(x) = max( \alpha x, x)
f(x)=max(αx,x)
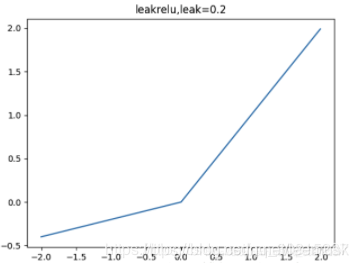
Relu 的变种,解决了负半轴的梯度消失问题,但是需要学习参数 α \alpha α,通常设为0.01或0.02
3.2.3. ELU
f
(
x
)
=
{
x
,
i
f
x
>
0
α
(
e
x
p
(
x
)
−
1
)
,
i
f
x
<
0
f(x) = \begin{cases} {x}, if \ x >0 \\{\alpha(exp(x)-1), if \ x < 0} \end{cases}
f(x)={x,if x>0α(exp(x)−1),if x<0

优点:
- 更接近0均值输出
- 与Leaky Relu相比,对噪声更具鲁棒性
缺点:
- 负区域饱和
3.2.4. 最大输出神经元 (Maxout Neuron)
m a x ( w 1 T x + b , w 2 T x + b ) max(w_1^Tx + b, w_2^Tx+b) max(w1Tx+b,w2Tx+b)
优点:
- 没有点乘操作
- 泛化ReLU和Leaky ReLU
- 没有饱和和梯度消失
缺点:
- 参数量翻倍
3.3 Batch Normalization
3.4 残差结构
3.5 其他方法
其他的方法有使用长短期记忆网络 LSTM、 权重正则化、预训练加finetunning、 使用梯度截断、使用权重正则化