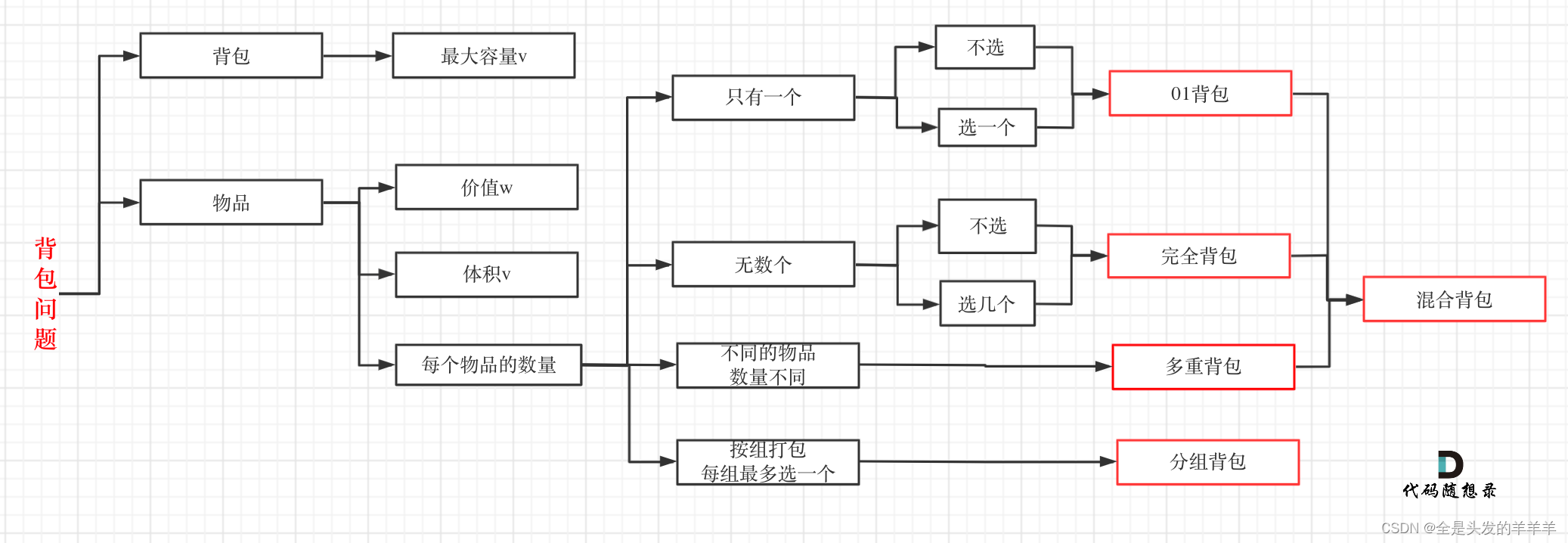
背包问题（动态规划

01背包是一种动态规划问题。动态规划的核心就是状态转移方程。

01背包问题可描述为如下问题：
有一个容量为V的背包，还有n个物体。现在忽略物体实际几何形状，我们认为只要背包的剩余容量大于等于物体体积，那就可以装进背包里。每个物体都有两个属性，即体积w和价值v。
问：如何向背包装物体才能使背包中物体的总价值最大？

01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品，每种物品有且只有一个（或者最多只能选取一个），并且有权值和体积两个属性。

在01背包问题中，因为每种物品只有一个（或者最多只能选取一个），对于第i个物品只需要考虑选与不选两种情况。那么选与不选的依据是什么呢？当然是该物品的性价比咯，而不是看当前背包所剩空间还能否装得下该物品。因为背包的剩余空间是不断根据选择的物品而变化的。

那么怎么判断选不选这个物品呢，就是看选了这个物品和不选这个物品背包的价值哪个大。就是max(不选的价值，选的价值)。

不选：背包的价值就不变，

选：背包的价值就等于这个物品的价值加上装了这个物品之后背包剩余空间用来装前（i-1）个物品的最大价值。

原始的 01背包

回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有两个方向推出来dp[i][j]，

由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]
由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

于其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了，i是物品，j是背包容量。

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

完全背包与01背包的区别就是完全背包的物品的数量无限并且可以重复选择。

那么就意味着第i种物品可以选取0~M%W[i]个，也就是说当选择第i种物品时，容量为j-W[i]的背包里可能已经装有该种物品了。

那么第二层循环的顺序就不能是从高到低了，而得是从低到高。

for(i=1;i<=n;i++)
		//for(j=m;j>=w[i];j--) //01背包 
		for(j=w[i];j<=m;j++)   //完全背包 
			f[j]=max(f[j],f[j-w[i]]+v[i]);
			
	printf("%d",f[m]);